海上風(fēng)力發(fā)電機組支撐結(jié)構(gòu)動力特性分析
陳 前, 付世曉,2, 鄒早建,2
(1.上海交通大學(xué) 船舶海洋與建筑工程學(xué)院,上海 200240;2.上海交通大學(xué) 海洋工程國家重點實驗室,上海 200240)
當今世界的能源主要來源于石油、煤等礦物質(zhì)燃料。隨著世界經(jīng)濟的發(fā)展,人們對能源的需求不斷增長,能源問題日益突出:一方面,礦物質(zhì)燃料能源為不可再生能源,正日益匱乏,面臨枯竭;另一方面,過分開發(fā)利用礦物質(zhì)燃料會導(dǎo)致一系列的環(huán)境問題,破壞地球生態(tài),威脅人類的生存。為此,全球正在進行第三次能源結(jié)構(gòu)調(diào)整,把從以石油、煤、天然氣為主的能源模式轉(zhuǎn)向以可再生清潔能源為基礎(chǔ)的可持續(xù)發(fā)展的能源模式。風(fēng)能是人類最早利用的能源之一,也是目前最具有競爭力和大規(guī)模開發(fā)利用前景的可再生能源。
隨著風(fēng)電開發(fā)技術(shù)的日趨成熟,風(fēng)電機組的單機容量不斷增大,風(fēng)機的尺寸和重量也都大幅度增加,對于機組支撐結(jié)構(gòu)的要求也在不斷提高。對于目前主流的三葉型水平軸單樁基礎(chǔ)式海上風(fēng)電機組而言,其支撐結(jié)構(gòu)包括塔筒和基礎(chǔ)兩部分,是整個風(fēng)電機組的主要承重結(jié)構(gòu)。在以往的工程實際中,支撐結(jié)構(gòu)由于疲勞而失效的情況較為少見,而由于支撐結(jié)構(gòu)振動引起的機組頂端位移過大,導(dǎo)致機組不能正常工作的事例較多。這使得海上風(fēng)電機組支撐結(jié)構(gòu)動力性能問題受到了越來越多的關(guān)注[1-3]。此外,為了降低海上風(fēng)力發(fā)電成本以取得更好的經(jīng)濟效益,目前多采用柔性支撐結(jié)構(gòu),甚至為超柔性支撐結(jié)構(gòu)。為避免風(fēng)輪轉(zhuǎn)動引起支撐結(jié)構(gòu)共振,支撐結(jié)構(gòu)固有頻率應(yīng)避開風(fēng)輪工作的激振頻率[4-5]。因此,對風(fēng)電機組支撐結(jié)構(gòu)固有頻率和振動響應(yīng)進行準確計算是保證風(fēng)機穩(wěn)定運行的重要前提。
海上風(fēng)電機組葉輪(包括輪轂)、機艙等稱為機組的上端結(jié)構(gòu),位于塔筒頂端,其質(zhì)量約占整個機組質(zhì)量的一半左右,稱為上端質(zhì)量。之前的研究在分析機組支撐結(jié)構(gòu)動力性能時,常將機組上端質(zhì)量的影響忽略,抑或是對其影響進行簡單的概括[6]。現(xiàn)用p-y曲線模擬海上風(fēng)電機組單樁基礎(chǔ)與海底土層之間的相互作用。同時,采用經(jīng)典的歐拉-伯努利梁理論,從理論上分析海上風(fēng)電機組支撐結(jié)構(gòu)固有頻率;并利用有限元法對某3 MW海上風(fēng)電機組支撐結(jié)構(gòu)建模計算,給出了上端質(zhì)量、整個機組重力和海水等對支撐結(jié)構(gòu)固有頻率的影響。另外,計算了機組突然停機和陣風(fēng)作用下支撐結(jié)構(gòu)響應(yīng)。計算結(jié)果表明:風(fēng)電機組上端質(zhì)量對支撐結(jié)構(gòu)固有頻率的影響很大,計算中應(yīng)予考慮,而機組重力對支撐結(jié)構(gòu)固有頻率的影響很小,計算中可以忽略;海水對支撐結(jié)構(gòu)固有頻率的影響隨著階次的增大而增大;當機組受到瞬態(tài)沖擊時,上端質(zhì)量相當于對支撐結(jié)構(gòu)響應(yīng)起到一個緩沖作用,而支撐結(jié)構(gòu)阻尼率主要影響響應(yīng)衰減速度,對響應(yīng)幅值影響不大。本文較全面地分析了海上風(fēng)電機組支撐結(jié)構(gòu)固有頻率和瞬態(tài)沖擊下支撐結(jié)構(gòu)響應(yīng),所得結(jié)果可為海上風(fēng)電機組支撐結(jié)構(gòu)設(shè)計提供參考。
1 數(shù)學(xué)模型
1.1 邊界約束
單樁基礎(chǔ)式海上風(fēng)電機組結(jié)構(gòu)的約束問題,實質(zhì)上就是研究基礎(chǔ)樁與土之間的相互作用。樁在水平載荷作用下發(fā)生變形,導(dǎo)致樁周土發(fā)生變形而產(chǎn)生土抗力,而這一土抗力又阻止樁的變形,這樣就使樁周土承擔(dān)了樁的水平載荷。當水平載荷較小時,土抗力由表層的土提供,以彈性變形為主,隨著水平載荷的增加,樁的變形增大,表層土逐漸產(chǎn)生塑性屈服,從而使水平載荷向更深的土層傳遞。
采用被廣泛應(yīng)用的p-y曲線來模擬海上風(fēng)電結(jié)構(gòu)基礎(chǔ)與土的相互作用。p-y曲線就是在水平力H的作用下,泥面以下深度為z處的土反力p與該點處樁的撓度y之間的關(guān)系曲線,水下軟粘土的p-y曲線經(jīng)驗公式如下[7,8]:
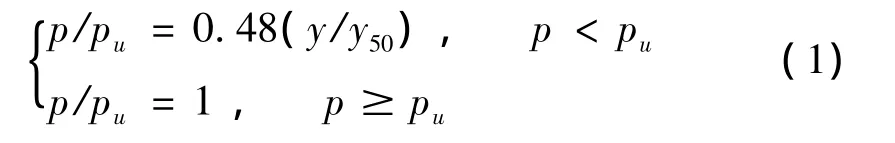
其中:
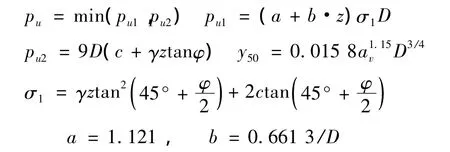
其中,c為土粘聚力,單位 kPa;γ為土的重度,單位kN/m3;z為泥面下深度,單位m;D為樁直徑,單位m;φ為摩擦角,單位(°);av為壓縮系數(shù),單位 MPa-1;pu為沿樁長單位長度上的極限水平土抗力,單位kN/m;y50為達到極限土抗力一半時的樁撓曲變形,單位m。
1.2 支撐結(jié)構(gòu)自由振動微分方程
由于單樁式海上風(fēng)電機組的支撐結(jié)構(gòu)屬于細長體,故采用不考慮截面剪切變形和轉(zhuǎn)動慣量的歐拉-伯努利梁理論[10]對其進行分析。
沿結(jié)構(gòu)高度方向取微段進行受力分析,如圖1。
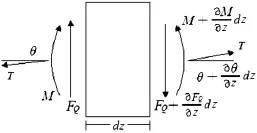
圖1 微段受力分析圖Fig.1 Force analysis of section
根據(jù)達朗貝爾原理,得到動力學(xué)方程為:

即:
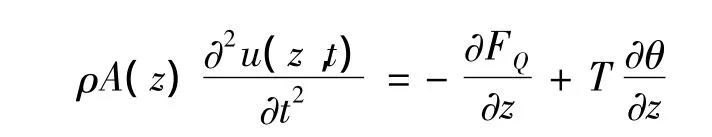
其中,ρ為材料密度,單位kg/m3;A(z)為截面積,單位m2;d z為微元長度,單位m;u(z,t)為撓度,單位m;FQ為截面剪力,單位N;T為所受軸向力,單位N;θ為截面轉(zhuǎn)角,單位rad。
對微元右截面取矩,得動力矩方程為:

其中,M為截面彎矩,單位N·m;由于θ與 d z為同階小量,上式略去高階小量后,為:
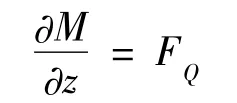
另外,根據(jù)材料力學(xué)[9]中彎矩與撓度之間的關(guān)系:
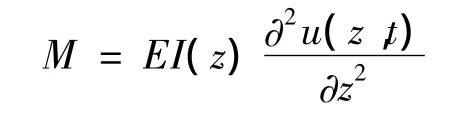
其中,E為材料的彈性模量,單位Pa;I(z)為截面的轉(zhuǎn)動慣量,單位m4。
得到支撐結(jié)構(gòu)受軸向拉力時的自由振動微分方程為:
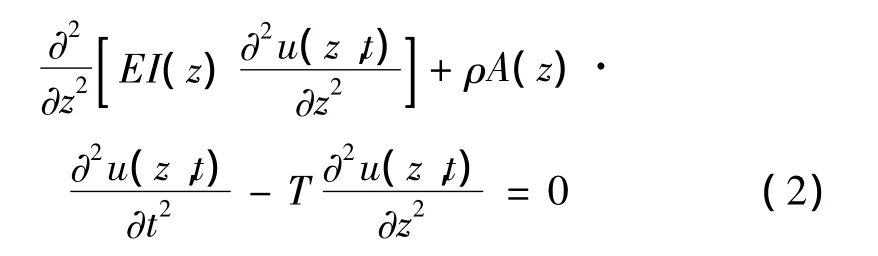
將方程解分離變量,令:

回代得:
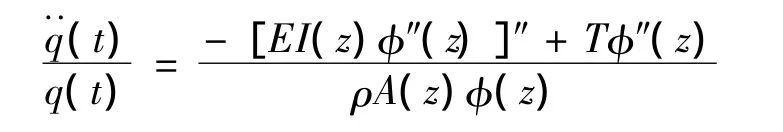
上式左端與空間變量z無關(guān),右端與時間t無關(guān),故只能等于一常數(shù),記作-ω2,則可導(dǎo)得:
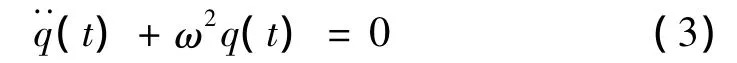
其通解為:q(t)=a sin(ωt+φ),ω為支撐結(jié)構(gòu)的固有頻率。
但方程:
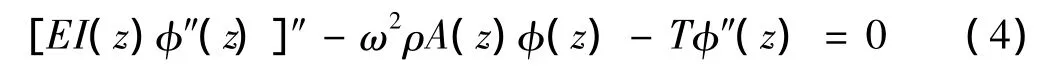
只有在幾種特殊的邊界條件下,且支撐結(jié)構(gòu)截面不變即I(z)和A(z)為常數(shù)時才能得到解析解。
1.3 支撐結(jié)構(gòu)有限元分析
采用有限單元法討論上述問題[10],將支撐結(jié)構(gòu)沿高度方向進行單元離散,得到單元剛度矩陣KE和單元質(zhì)量矩陣Me。然后,根據(jù)單元節(jié)點位移協(xié)調(diào)條件和力平衡條件,將單元的剛度矩陣和質(zhì)量矩陣組裝成結(jié)構(gòu)總剛度矩陣K和結(jié)構(gòu)總質(zhì)量矩陣M。得:
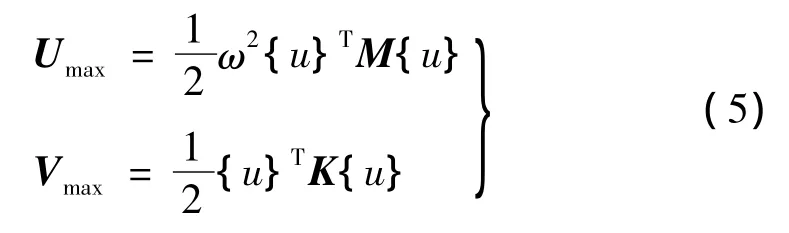
其中,{u}為節(jié)點位移列陣。
根據(jù) Umax=Vmax,則有,結(jié)合邊界條件可得到支撐結(jié)構(gòu)固有頻率。而后,將得到的第i階固有頻率得到相當?shù)牡趇階模態(tài) φi。
另外,當支撐結(jié)構(gòu)受到軸向壓力時,T用-T代替,當支撐結(jié)構(gòu)不受軸向力時T取零。若結(jié)構(gòu)中存在集中質(zhì)量,則僅需對結(jié)構(gòu)總質(zhì)量矩陣M進行相應(yīng)的簡單修改,獲得新的結(jié)構(gòu)總質(zhì)量矩陣代入計算即可。
1.4 支撐結(jié)構(gòu)動力響應(yīng)微分方程
當受到瞬態(tài)激勵作用時,支撐結(jié)構(gòu)的動力微分方程[8]為:
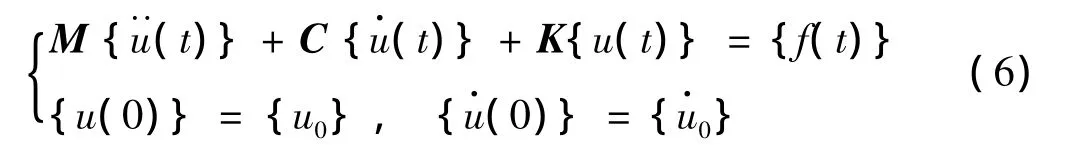
2 支撐結(jié)構(gòu)和環(huán)境參數(shù)
本文以某3 MW海上風(fēng)電機組為例,圖2為其支撐結(jié)構(gòu)簡圖。假設(shè)其連接平臺質(zhì)量為6 t,葉輪半徑R為40 m,額定風(fēng)速 v為 13 m/s,根據(jù)經(jīng)驗可取風(fēng)輪的軸向推力系數(shù) CF為8/9,空氣密度 ρ0為 1.29 kg/m3。則可得到機組在額定工況下的風(fēng)輪軸向力[11]:

本文通過定義不同大小的上端質(zhì)量來分析其對支撐結(jié)構(gòu)動力性能的影響,上端質(zhì)量m0范圍為0 t~120 t。此外,以海平面為參考點,表1給出了該海上風(fēng)電機組的支撐結(jié)構(gòu)參數(shù);海底泥層的土工參數(shù)如表2所示。

圖2 海上風(fēng)電機組支撐結(jié)構(gòu)Fig.2 Support structure of offshore wind turbine
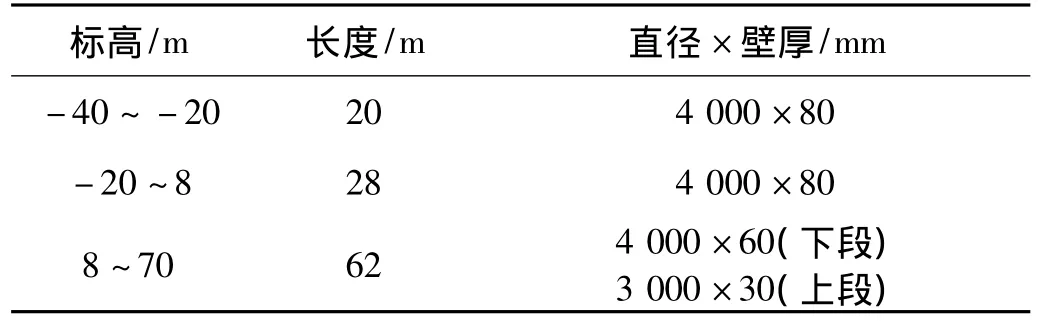
表1 海上風(fēng)電機組支撐結(jié)構(gòu)參數(shù)表Tab.1 Parameters of offshore wind turbine support structure

表2 土工參數(shù)Tab.2 Geotechnical parameter
3 海上風(fēng)電機組支撐結(jié)構(gòu)動力特性分析
通常情況下,風(fēng)電機組的風(fēng)輪工作頻率約為0.2 Hz~0.4 Hz,風(fēng)輪3 倍工作頻率約為 0.6 Hz~1.2 Hz。因此,在風(fēng)電機組設(shè)計中為保證安全性,避免風(fēng)輪和支撐結(jié)構(gòu)發(fā)生共振,應(yīng)對影響支撐結(jié)構(gòu)動力特性的幾個因素進行分析。
3.1 上端質(zhì)量對支撐結(jié)構(gòu)動力特性影響
對海上風(fēng)電機組支撐結(jié)構(gòu)進行模態(tài)分析,并令其固有頻率為fi,j,其中i表示支撐結(jié)構(gòu)固有頻率階次,j表示上端質(zhì)量 m0大小(j=0,10,20,…,120),并引入?yún)?shù) ηi=fi,j/fi,0。由此看出固有頻率 fi,j和參數(shù) ηi均為上端質(zhì)量的函數(shù),故有支撐結(jié)構(gòu)1階固有頻率和2階固有頻率隨上端質(zhì)量變化關(guān)系分別如圖3和圖4,參數(shù)ηi與上端質(zhì)量之間的關(guān)系如圖5。由圖3和圖4可看出,隨著上端質(zhì)量的增大,支撐結(jié)構(gòu)固有頻率相應(yīng)變小,在不考慮上端質(zhì)量時支撐結(jié)構(gòu)1階固有頻率和2階固有頻率分別為0.564 Hz和2.318 Hz,而當上端質(zhì)量為120 t時,支撐結(jié)構(gòu)的1階固有頻率和2階固有頻率分別為0.353 Hz和1.799 Hz。另外,由圖5可以看出:① 隨著上端質(zhì)量增大,整個機組的支撐結(jié)構(gòu)趨于柔性化,固有頻率相應(yīng)變小;② 隨著上端質(zhì)量增大,其對支撐結(jié)構(gòu)固有頻率的影響相對減小;③ 機組上端質(zhì)量對支撐結(jié)構(gòu)固有頻率影響隨著階次增加有所減小。由此,為保證機組的安全性,在工程設(shè)計中應(yīng)考慮上端質(zhì)量對支撐結(jié)構(gòu)固有頻率的影響。
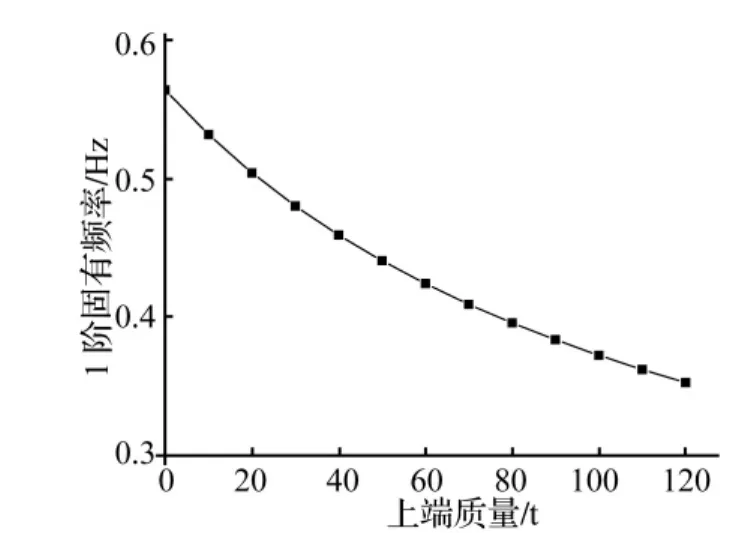
圖3 支撐結(jié)構(gòu)1階固有頻率Fig.3 The first order natural frequency of support structure
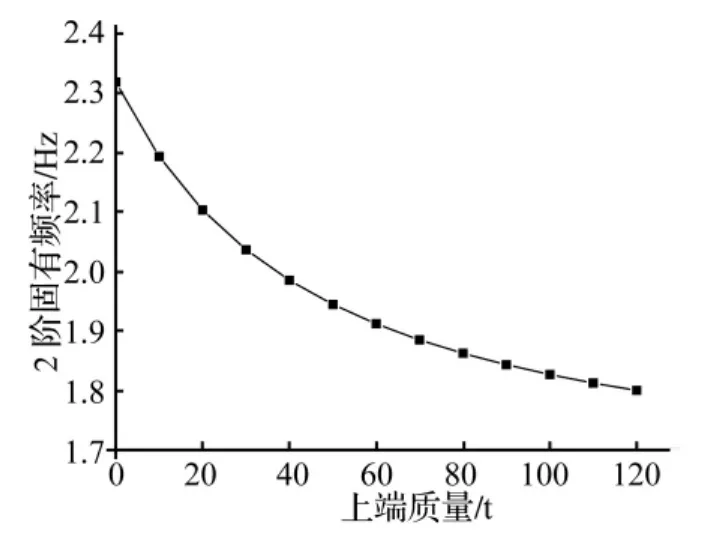
圖4 支撐結(jié)構(gòu)2階固有頻率Fig.4 The second order natural frequency of support structure
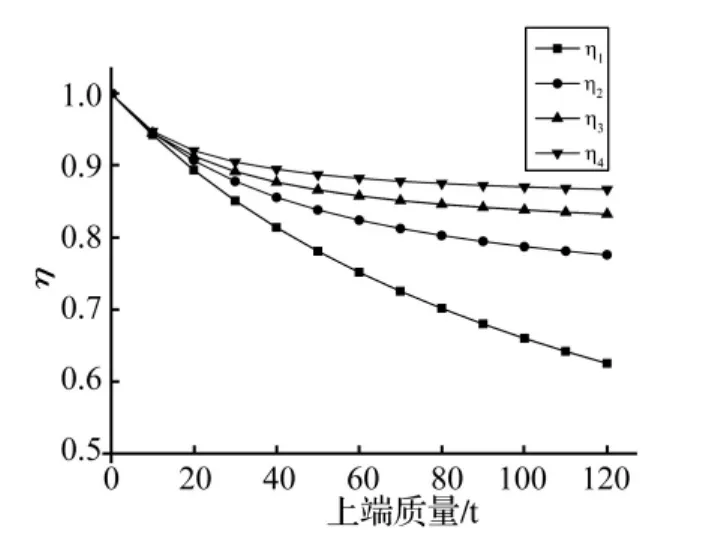
圖5 η與上端質(zhì)量的關(guān)系Fig.5 The relationship between ηand upper quality
3.2 風(fēng)電機組重力對支撐結(jié)構(gòu)動力特性影響
風(fēng)電機組的重力包括風(fēng)輪、機艙等上端結(jié)構(gòu)的重力和支撐結(jié)構(gòu)自身的重力,等效于支撐結(jié)構(gòu)受到軸向壓力。因此在考慮重力影響時,所得的支撐結(jié)構(gòu)固有頻率應(yīng)小于不考慮重力的情況所得的結(jié)果。令考慮重力影響且考慮上端質(zhì)量影響時所得支撐結(jié)構(gòu)第i階固有頻率為,由表3可看出機組重力對支撐結(jié)構(gòu)固有頻率影響很小,對高階固有頻率更是基本沒影響。因此,在工程中為簡化計算可以不考慮機組重力對支撐結(jié)構(gòu)固有頻率的影響。
3.3 海水對支撐結(jié)構(gòu)動力特性影響
相比于陸上風(fēng)電機組,海上風(fēng)電機組的支撐結(jié)構(gòu)有相當一段浸沒在海水中,若令不考慮海水影響時支撐結(jié)構(gòu)第i階固有頻率為,分別在不考慮支撐結(jié)構(gòu)上端質(zhì)量和上端質(zhì)量為120 t兩種情況下討論海水對支撐結(jié)構(gòu)固有頻率影響。由表4可看出,海水的存在對支撐結(jié)構(gòu)的1階固有頻率基本沒影響,而使得支撐結(jié)構(gòu)高階固有頻率降低,相當于抑制作用,并且隨著固有頻率階次增大這種作用越明顯。所以在對支撐結(jié)構(gòu)進行高階模態(tài)分析時,海水的影響不能忽略。

表3 重力對支撐結(jié)構(gòu)固有頻率影響Tab.3 The influence of gravity on support structure natural frequency

表4 海水對支撐結(jié)構(gòu)固有頻率影響Tab.4 The influence of seawater on the support structure natural frequency
4 瞬態(tài)沖擊載荷作用下支撐結(jié)構(gòu)動力響應(yīng)
假設(shè)機組工作的額定風(fēng)速為13 m/s,支撐結(jié)構(gòu)的結(jié)構(gòu)阻尼率為0.05。在額定狀態(tài)下,風(fēng)機相當于在支撐結(jié)構(gòu)頂端受一軸向靜推力作用,假設(shè)在10s時風(fēng)機突然停機,相當于在此時刻支撐結(jié)構(gòu)頂端軸向推力驟減為0,結(jié)構(gòu)開始自由振蕩。若取時間步長為0.25 s,則支撐結(jié)構(gòu)頂端水平位移時間歷程曲線見圖6。
此外,假設(shè)風(fēng)機在10 m/s風(fēng)速下穩(wěn)定工作,此時支撐結(jié)構(gòu)頂端水平位移也為一穩(wěn)定值。在10 s時受到一陣風(fēng)作用,作用時間為3 s,風(fēng)速線性增大到13 m/s,而后驟減到10 m/s。若取計算時間步長為0.25 s,則支撐結(jié)構(gòu)頂端水平位移時間歷程曲線見圖7。
由圖6和圖7可以看出,當風(fēng)機受到瞬間沖擊作用時:① 上端質(zhì)量使得支撐結(jié)構(gòu)頂端水平位移響應(yīng)幅值有所增大;② 上端質(zhì)量使得支撐結(jié)構(gòu)響應(yīng)衰減率有所減小;③ 上端質(zhì)量使得支撐結(jié)構(gòu)響應(yīng)周期有所增大。由此,可以看出風(fēng)電機組上端質(zhì)量在機組受到瞬態(tài)沖擊時相當于一個能量儲存器,對支撐結(jié)構(gòu)響應(yīng)起到一個緩沖作用。
圖8給出了支撐結(jié)構(gòu)受到瞬態(tài)沖擊時頂端位移響應(yīng)幅值和結(jié)構(gòu)阻尼率之間的關(guān)系。通過計算發(fā)現(xiàn),當支撐結(jié)構(gòu)受到瞬態(tài)沖擊載荷作用時,結(jié)構(gòu)阻尼率對頂端位移響應(yīng)幅值影響并不大,其主要影響支撐結(jié)構(gòu)響應(yīng)的衰減速度。另外,通過計算發(fā)現(xiàn),相比支撐結(jié)構(gòu)自身的結(jié)構(gòu)阻尼率,海水對其動力響應(yīng)的阻滯作用為小量。故在計算支撐結(jié)構(gòu)動力響應(yīng)時,可忽略海水的阻滯作用。
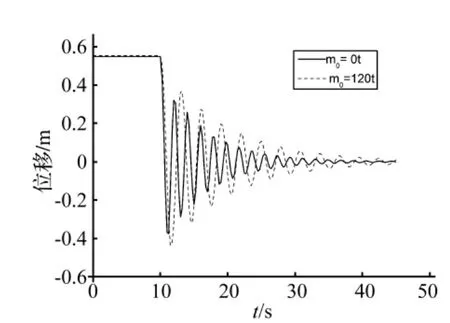
圖6 突然停機時支撐結(jié)構(gòu)頂端位移響應(yīng)曲線Fig.6 Curve of the top displacement of support structure under a sudden shutdown
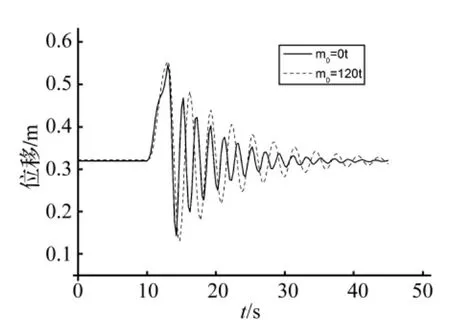
圖7 陣風(fēng)作用時支撐結(jié)構(gòu)頂端位移響應(yīng)曲線Fig.7 Curve of the top displacement of support structure under a gust load

圖8 支撐結(jié)構(gòu)阻尼率與頂端位移響應(yīng)幅值關(guān)系Fig.8 Relation between structure damping ratio and top displacement amplitude of support structure
5 結(jié)論
本文對海上風(fēng)電機組支撐結(jié)構(gòu)進行了模態(tài)分析,并分析了上端質(zhì)量、機組重力和海水等因素對支撐結(jié)構(gòu)固有頻率的影響。此外,以機組在額定工況下突然停機為例分析了支撐結(jié)構(gòu)受到瞬態(tài)沖擊時上端質(zhì)量對結(jié)構(gòu)動力響應(yīng)的影響。通過本文研究得到以下幾點結(jié)論:
(1)海上風(fēng)電機組葉輪、機艙等上端結(jié)構(gòu)質(zhì)量對支撐結(jié)構(gòu)低階固有頻率影響很大,在設(shè)計過程中對支撐結(jié)構(gòu)進行固有頻率計算時應(yīng)考慮上端質(zhì)量影響,避免支撐結(jié)構(gòu)與風(fēng)輪工作頻率和風(fēng)輪3倍工作頻率發(fā)生共振。
(2)海上風(fēng)電機組重力對支撐結(jié)構(gòu)固有頻率影響不大,并且隨著固有頻率階次增大,重力的影響越來越小,因此在工程設(shè)計中計算機組支撐結(jié)構(gòu)固有頻率時可以不考慮機組重力。
(3)海水對支撐結(jié)構(gòu)固有頻率的影響隨著固有頻率階次的增加急劇增大。若不考慮海水的阻滯影響,所得的支撐結(jié)構(gòu)高階固有頻率將要比實際值大很多。因此在工程設(shè)計中,海水對支撐結(jié)構(gòu)固有頻率的影響不能忽略。
(4)當受到瞬態(tài)沖擊載荷作用時,上端結(jié)構(gòu)質(zhì)量相當于一個緩沖裝置,使得支撐結(jié)構(gòu)響應(yīng)的衰減率略為減小,而衰減周期略為增大。
(5)當受到瞬態(tài)沖擊載荷作用時,支撐結(jié)構(gòu)阻尼率對頂端位移響應(yīng)幅值影響并不大,其主要影響支撐結(jié)構(gòu)響應(yīng)的衰減速度。
[1] 李宗福,張有聞,白云飛.風(fēng)力發(fā)電機塔架設(shè)計綜述[J] .低溫建筑技術(shù),2007,4:79-80.
[2] Murtagh P J,Basu B,Broderick B M.Along-wind response of a wind turbine tower with blade coupling subjected to rotationally sampled wind loading[J] . Engineering Structures,2005,27:1209 -1219.
[3] Bazeos N,Hatzigeorgiou G D.Static,seismic and stability analyses of a prototype wind turbine steel tower[J] .Engineering Structures,2002,24:1015 -1025.
[4] 趙榮珍,呂 鋼.水平軸風(fēng)力發(fā)電機塔架的振動模態(tài)分析[J] .蘭州理工大學(xué)學(xué)報,2009,35(2):33-36.
[5] 黃東勝,王朝勝,鄒富順,等.風(fēng)力機塔架模態(tài)分析及應(yīng)用[J] .裝備制造技術(shù),2009,9:19-21.
[6] 王永智,陶其斌,周必成.風(fēng)力機塔架的結(jié)構(gòu)動力分析[J] .太陽能學(xué)報,1995,16(2):162-169.
[7] 程澤坤.基于P-Y曲線法考慮樁土相互作用的高樁結(jié)構(gòu)物分析[J] .海洋工程,1998,16(2):73-82.
[8] 蘇靜波,邵國建,劉 寧.基于P-Y曲線法的水平受荷樁非線性有限元分析[J] .巖土力學(xué),2006,27(10):1781-1785.
[9] 劉鴻文.材料力學(xué)[M] .北京:高等教育出版社,2004.
[10] 胡海巖.機械振動基礎(chǔ)[M] .北京:北京航空航天大學(xué)出版社,2005.
[11] 勒古里雷斯 D,著.風(fēng)力機的理論與設(shè)計[M] .施鵬飛,譯.北京:機械工業(yè)出版社,1982.

