關于高等數學中兩個問題的探討

司志本， 李春光

（1.河北民族師范學院 初等教育系，河北 承德 067000 2.河北民族師范學院 科研處，河北 承德 067000）

關于高等數學中兩個問題的探討

司志本1， 李春光2

（1.河北民族師范學院 初等教育系，河北 承德 067000 2.河北民族師范學院 科研處，河北 承德 067000）

分段函數和積分上限函數，是高等數學中比較重要的兩類函數.分段函數在分界點處的導數和積分，是學生感到比較棘手的內容，這就需要教師在內容的解讀以及教學方法的選取上，要根據學生的實際情況進行科學的處理；積分上限函數，是一個用積分形式給出的函數，深入挖掘這個函數的潛在功能，對于學生深刻理解微積分的概念是十分有益的.

分段函數；積分上限函數；導數；積分

在高等數學中，有許多內容都要涉及到分段函數和積分上限函數，而學生在解決這兩類函數的相關問題時，往往會感到無從下手.本文將對這兩類函數的相關問題做一點探討，相信對學生能夠起到一定的指導作用.

1. 關于分段函數的導數和積分

分段函數是一類常見的并且十分重要的函數，它的明顯特征就是“分段”，它在分界點處的一些運算和性質，對于初學者來說，需要謹慎處理.

1.1 對分段函數定義的理解

分段函數是指在自變量的不同變化范圍中，對應法則用不同式子來表示的函數(注：本文中的分段函數均指一元函數)。分段函數雖然有時也可以用一個式子表示出來，例如，分段函數可以用一個式子表示為但是，為了研究方便，我們往往還是用幾個表達式來表示，而不刻意追求形式上的簡單.

我們知道，初等函數在它的定義區間內是連續的.因為分段函數的分段點往往是間斷點，所以，在有些情況下，分段函數在整個定義區間上不是初等函數.

因為分段函數的關鍵特征是“分段”，所以，在一般情況下，分段函數的圖象是由若干段曲線組成的.例如，函數

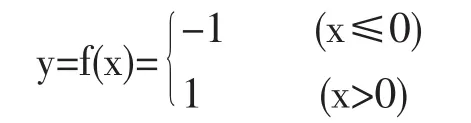
的圖象是以點（0，-1）和點（0，1）（不含此點）為始點，分別向左和向右的兩條水平射線.

1.2 分段函數的導數

一般來說，求分段函數的導數可以分兩步進行，第一步，先求出函數在去掉分界點以后的各個區間上的導數；第二步，再研究函數在分界點處的導數情況.在各個小區間上的導數可以根據導數的定義、公式和性質等，采用多種方法去求；而在分界點處的導數，一般需要先研究函數在該點的單側導數（左導數和右導數）.具體說來，如果在該點存在單側導數，那么就先求出函數在該點處的單側導數；然后再根據單側導數的情況，判斷函數在該點是否可導；若可導，再進一步求出導數.

解：先將函數f(x)寫為分段函數的形式.

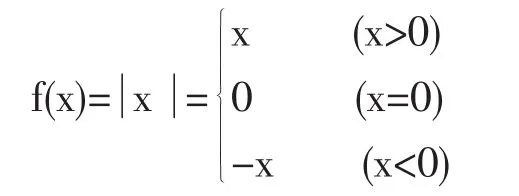
當x＞0時，有f′(x)=1；當x＜0時，有f′(x)=-1；當x=0時，由左、右導數的定義有

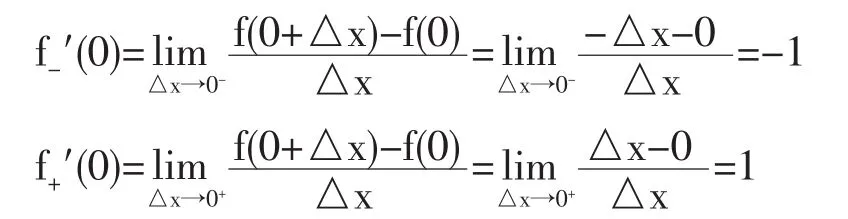
因為f-′(0)≠f+′(0)，所以，函數在x=0點處不可導.

有時也可以根據導數定義直接求出函數在分界點處的導數.

解：當x≠0時，有

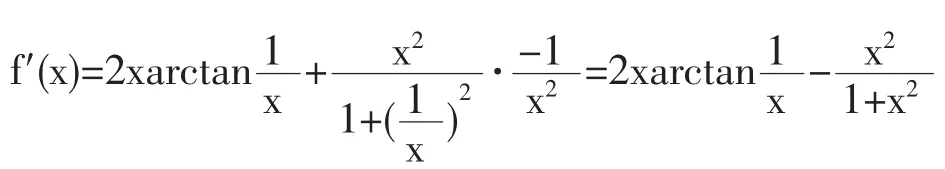
當x=0時，由導數定義有

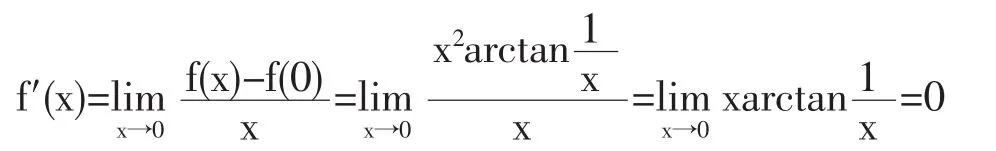
1.3 分段函數的不定積分

在求分段函數的不定積分時，首先要求出分段函數在各個小區間上的不定積分，這些積分中包含著若干個積分常數，如果被積函數在所有的分界點都是連續的，那么就可以根據不定積分（原函數）的連續性，找出這些積分常數之間的關系，最后得到只含有一個積分常數的不定積分；如果被積函數在某些分界點不連續，那么最后的積分結果可能不止含有一個積分常數，而是含有幾個獨立的積分常數.

因為被積函數f(x)在區間(-∞,+∞)上連續，所以，根據原函數的定義可知，f(x)的原函數也在該區間上連續.

在例3中，因為f(x)在整個定義區間(-∞,+∞)上是連續的，所以，最后的積分結果中只含有一個積分常數.

解：容易知道，分段點x=0是f(x)的第一類間斷點（即函數f(x)在x0點的左右極限都存在）；分段點x=1是f(x)的連續點.先分別求出f(x)在區間(-∞,0)，（0，1）和(1,+∞)上的不定積分：

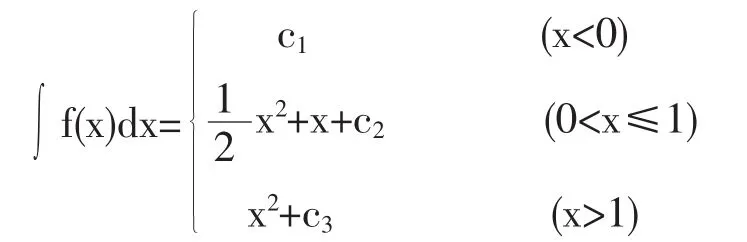
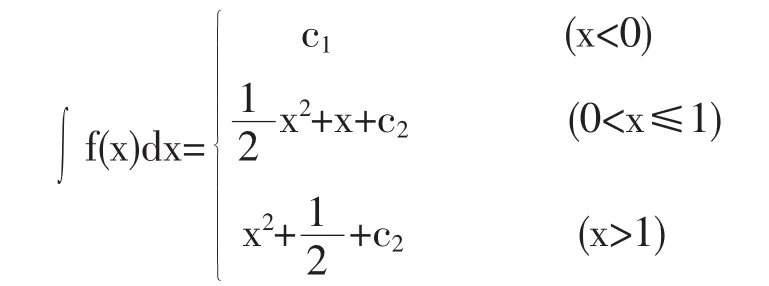
由例4可知，在分段函數的不定積分中，如果分段點是不連續點，則積分常數可能不止一個.

1.4 分段函數的定積分

與不定積分相比較，分段函數的定積分就顯得簡單多了.定積分的定義告訴我們，有限個間斷點不影響定積分的值，所以，只要分段函數的定積分存在，我們就可以以分界點為界點，把原積分區間劃分為若干個小的積分區間，先求出函數在每一個小區間上的定積分，然后再對這些積分值求和即可.

解：將被積函數寫為分段函數的形式：

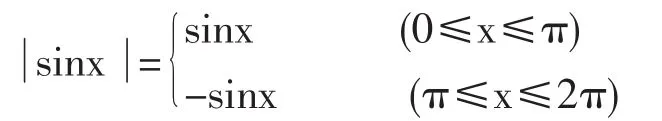
以x=π為界點，將積分區間[0，2π]拆為兩個小區間[0，π]，[π，2π]，則有

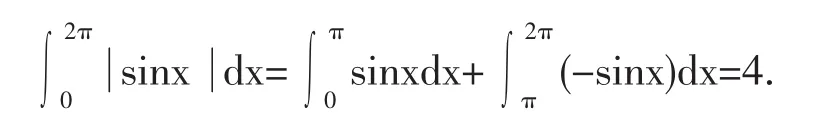
2. 關于積分上限函數的導數

積分上限函數，是一個用積分形式給出的函數，深入挖掘這個函數的潛在功能，對于深入理解微分和積分的概念是十分有益的.我們先給出積分上限函數的定義以及與之相關的一個定理.

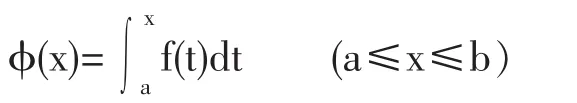
為積分上限函數，也稱變上限函數.

定理：若函數f(x)在區間[a,b]上連續，則積分上限函數

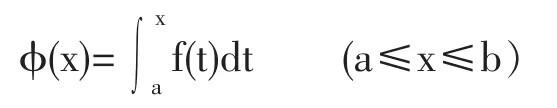
在[a,b]上可導，其導數為

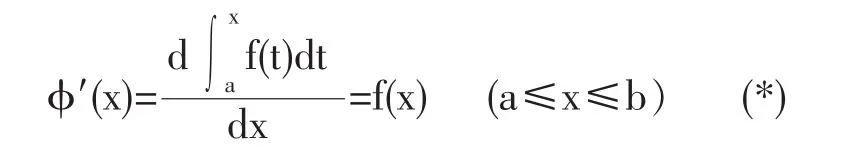
2.1 幾個積分表達式

上面的（*）式體現了積分上限函數的一個明顯特征：即對一個函數先積分后微分，其作用相互抵消.這個特征可以看作是不定積分性質的一種推廣.受（*）式啟發，我們從一個基本的積分表達式出發，把這個積分中三個含t的位置，分別用一個x，兩個x，三個x替換，對于得到的表達式再分別對x和t求導，研究一下這些導數的情況.在下面的討論中，我們假設所涉及的f(x)的導數和積分都是存在的.

最基本的積分為（三個位置都是t，不含x）：

把（1）式中1個位置的t換為x，可以得到下面三個積分：

CRISPR/Cas9系統也有局限性。如存在一定的脫靶效應。CRISPR/Cas9系統的特異性取決于sgRNA上的識別序列。為了避免脫靶效應，有必要將Cas9引導至其基因組中精確靶標的sgRNA。為了確保Cas9的靶向活性和正常功能，使用Ⅱ型CRISPR/Cas系統和Cas9表征的研究已經證明需要與靶基因序列完美匹配[26-28]。有學者研發了很多軟件輔助CRISPR/Cas9系統快速篩選特定基因序列靶點，有針對性地避開可能脫靶的位點，從而降低甚至消除脫靶現象[29]。

把（1）式中2個位置的t換為x，可以得到下面三個積分：

把（1）式中的三個t都換為x，可以得到下面一個積分：

把（1）式中的積分上限換為常數a，可以得到下面一個積分：

2.2 對x的導數

現在我們分別討論上面9個積分對x的導數。

(2)式中的積分對x的導數，上面的定理給出了結論，即

（4）式中的積分變量是x，因此，這個積分實際上是被積函數為常數的定積分，即

（5）式中的積分變量是t，被積函數f(x)可以視為常數，即再對x求導,則有

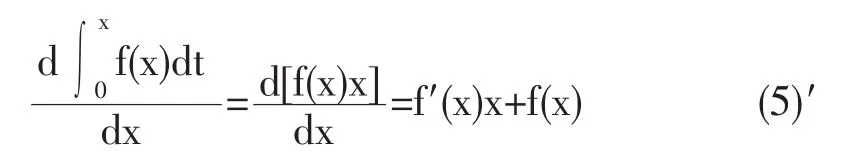
（6）式中的積分變量是x，被積函數f(t)可以視為常數，即它對x的導數為

（8）式中的積分變量是x，從本質上講，與（1）式沒區別，但是，這個積分結果是x的函數，所以，對x的導數為

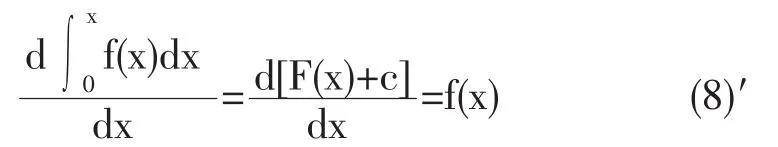
其中，F(x)是f(x)的一個原函數.

（9）式中的a是一個常數，這個積分就是通常意義下的定積分，其積分結果是一個常數，所以，對x求導的結果是0，即

3. 對t的導數

關于（1）—（9）式中的9個積分對t的導數，完全可以仿照上面的方法進行討論，其結果與對x求導的結果十分相似，此處不再贅述.

[1]華東師范大學數學系.高等數學（上）[M].上海：華東師范大學出版社，1998,(8)

[2]西北工業大學高等數學教研室.高等數學中的典型問題與解法[M].上海：同濟大學出版社，2001,(6)

[3]呂通慶.數學分析中一些重要概念及其矛盾概念[M].北京：高等教育出版社，1979,(3)

O13

A

2095-3763（2012）02-0073-03

2011-11-20

司志本（1959-），男，河北興隆人，河北民族師范學院初等教育系教授。