延誤航班機場場面滑行優化調度策略研究＊

柳 青 李春玲 宋祥波

（南京航空航天大學民航學院1） 南京 210016） （中國民航大學經管學院2） 天津 300300）

樞紐機場場面控制問題（ASMCP）的核心是航空器路徑規劃及停機位分配.目前國外研究關注較多的是自動場面控制系統［1－2］、啟發式算法求解航班調度次序［3］、場面運行控制和地面等待著陸［4］，以及對多跑道系統（阿姆斯特丹機場）的復雜調度以及高密度航班（達拉斯沃斯堡機場）的實證分析.國內現階段研究主要使用多Agent仿真建模、TDSP動態算法等解決航空器路徑規劃和優化問題［5］.本文將延誤航班按路徑屬性歸類，依照流水車間作業調度方式對其進行滑行調度，是機場控制區調度作業的最新探索，能豐富處理延誤航班應急調度的策略，有較為重要的實際意義.

1 延誤航班滑行調度建模

1.1 問題分析

延誤航班應急調度是指在出現天氣、管制等原因后，高峰小時內大量的進港航班不能按計劃到達時間（ETA）降落機場，滑入目標停機位.在出現航班不正常運行的緊急情況時，制定應急調度預案，重新分配調度方案，安排更高效的調度計劃是解決地面擁堵的重要途徑.調度航班滑行必須遵守相關的安全標準，否則，遇到時刻變化和各種特殊緊急情況，航空器滑行容易產生三類場面沖突［6］，如圖1所示.

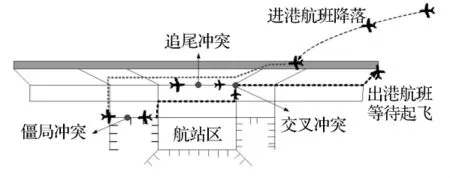
圖1 航班調度過程及滑行三類沖突

航班調度除推入推出目標停機位可能不同外，有大量航班具有同樣的滑行路徑.正常情況下，不同航空公司飛往不同目的地的不同航班交錯進離港.一旦出現航班延誤，既有航班計劃將被打亂，機場在效率和安全壓力下，可以考慮選擇更簡單、更快速的應急調度策略，流水作業法完全可以模擬車間流水線調度，將具有相同滑行路徑的航班進行聚類，統一安排調度，解決大面積延誤航班調度同時，有效規避滑行沖突，見圖2.

1.2 假設條件

延誤航班調度發生于特殊情況，模型建立需要滿足一定的假設前提：（1）在時間（0，T）內有一組待降落的航班｛f1，f2，…，fi｝?Aarr和一組等待 起飛的航班｛f1，f2，…，fj｝?Adep由于特殊原因發生延誤；（2）受所帶油量限制，進港航班在空中等待落地的時間有限.同樣，離港航班在關艙門后，發動機處于運轉狀態，不會無限期等待，離港等待滑行的時間有限；（3）在一個固定時段內，滑行邊上任意節點一次只能通過一架航空器；（4）在一個固定時段內，一架航空器只能在一條滑行邊上滑行.

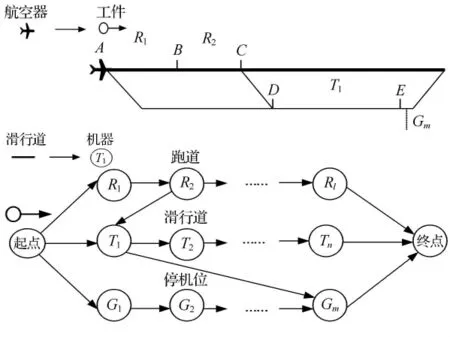
圖2 航空器滑行調度轉化為流水車間調度過程

1.3 相關符號及模型建立

將經典車間流水線作業的思想應用于應急航班調度建模，具體過程可描述為：在應急高峰時段內有n個需要調度航班fi（i＝1，2，…，n）在m 條滑行道邊Rj（j＝1，2，…，m）上滑行，這n個航班依據路徑屬性可以歸類成l組航班簇.在一個航班簇內，航班fi的滑行路徑Ri，j（j＝1，2，…，ml），航班滑行路徑Ri，j必須通過滑行邊Rj，滑行時間記為pi，j.調度目標是在滿足路徑的要求下，為每架航空器尋找到一條有時間限制的路線，最終使所有航空器總調度滑行時間最小，由此建立延誤航班流水調度模型：

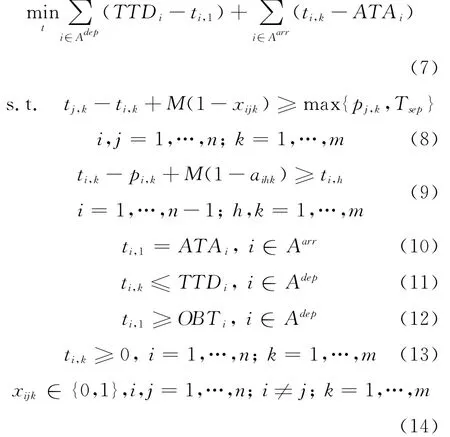
模型中，決策變量ti，k為航班i在滑行道Rk上完成滑行的時間；pi，k為航空器i在Rk邊上的滑行時間；xijk為二進制決策變量，表示指示變量.如果航班fi在航班fj之前在Rk上滑行，則xijk＝1，否則，xijk＝0；aihk為二進制決策變量，表示指示系數，若航空器i在滑行邊h上滑行的次序先于滑行邊k，那么aihk＝1，否則記為0；M 為一充分大的正整數；Tsep為不同機型之間按照規定要求的滑行間隔時間，根據不同重量機型選取不同的間隔距離值，用公式Tsep＝dsep／ˉv來計算兩架飛機最小時間間隔，ˉv取值飛機的平均速度.ATAi為到達航班fi的實際降落時間；OBTi為起飛航班撤輪檔時間，TTDi為離港航空器的結束滑行的起飛時間.

目標函數（7）指調度優化的總目標是所有進離港航空器調度滑行時間最少；約束（8）為航空器通過滑行邊的次序，除了滿足滑行時間外，還需要符合民航局規定的最小安全間隔；約束（9）為航空器在不同滑行邊上的滑行順序；約束（10）為降落航班的實際到達時間，也即起始滑行時間；約束（11）為離港航班的實際起飛時間；約束（12）為每架航空器必須降落到地面或者撤開輪檔才能開始滑行；約束（13）為對滑行完成時間的正數約束.航班預計降落時間ATAi和撤輪檔時間OBTi由空管調度給出時間表；約束（14）為對二進制變量的描述.

2 多粒子群求解算法設計

2.1 粒子群算法求解滑行調度

粒子群算法（particle swarm optimization，PSO）是Kennedy和Eberhart在1995年提出的群智能優化算法，針對NP復雜問題求解，粒子群算法有時間和效率的優勢［7－8］，粒子群算法求解調度問題的主要步驟包括：

1）編碼機制 首先對模型的參數進行編碼.由于調度是基于操作為基礎，粒子的順序代表了調度順序.用d＝n×m表示微粒的位置矢量，一個粒子可以表示為d維向量，每架航空器均會出現m次.將微粒轉化為有序的操作表，再根據每架航空器滑行時間進行調度，進而產生調度方案.舉一個3架進場航空器在5條滑行邊上滑行的例子，粒子位置 X＝［1，2，3，4，5，2，3，1，5，4，4，1，5，3，2］，根據航空器滑行次序（見表1），路徑R1的通過順序是J1－J2－J3，路徑2的調度次序是J2－J1－J3.

表1 航空器滑行次序

2）適應度函數 適應度函數用來評價粒子的性能，函數目標是最小化調度時間，考慮到航空器的安全間隔因素，也就是約束條件（8）.因此，算法用目標函數

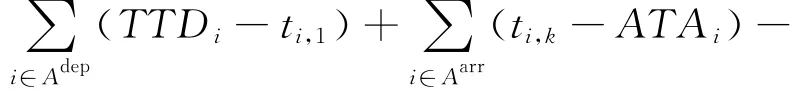
M（1－xijk）×min｛tj，k－ti，k－pj，k－Tsep，0｝作為候選方案的適應度函數，其中M（1－xjk）×min｛tj，k－ti，k－pj，k－Tsep，0｝作為約束條件放入到目標函數的懲罰項，一旦最小安全時間間隔小于規定值，則粒子的適應度函數加上無限大的正數項，可以避免進入下一次迭代.

2.2 多粒子群（CPSO）粒子群算法

多粒子群算法步驟如下.

步驟1 根據初始調度計劃，計算各航空器在各自路徑集Ri上的理想滑行時間.

步驟2 根據延誤航班的滑行路徑屬性進行聚類，同時考慮起降時刻間隔滿足等待時間約束的一類航班劃分為一組航班簇.

步驟3 設置2層粒子參數，全局最優粒子種群和5個子種群，計算初始子目標值.

步驟4 從5個最優子種群中找出最優適應度函數值Ztemp與當前全局最優適應度最優值進行比較，如果優于，則用新的適應度函數值代替前一輪的最優值.用相應新粒子代替原來的粒子，得到此狀態下的每個粒子的個體最優解Xpi.

步驟5 在最優種群的基礎上重新產生5個子種群，利用式（8）、（9）移動粒子，產生新的粒子群，重復步驟5，直至完成設定的迭代次數.

步驟6 將Ztemp與目前的適應度最優值進行比較，如果優于，則用新的適應度函數值代替前一輪的最優值.用相應新粒子代替原來的粒子，得到此狀態下的每個粒子的個體最優解Xpi.

步驟7 計算調度時間，得到調度方案.

3 算例分析

依算法步驟，首先根據延誤航班進離港調度路徑和停機位進行屬性聚類，延誤航班滑行路徑可以分為6組待調度的航班簇，見表2.每組航班簇有相同或者相近的停機位，再對6組航班簇進行滑行調度優化.

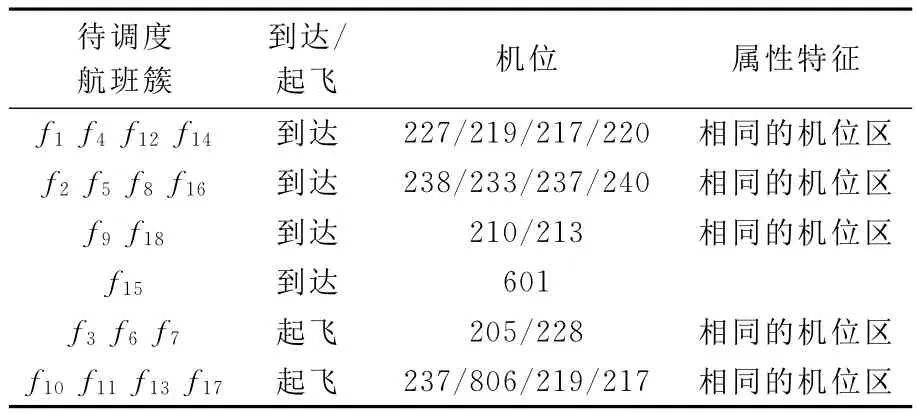
表2 聚類航班簇流水車間調度

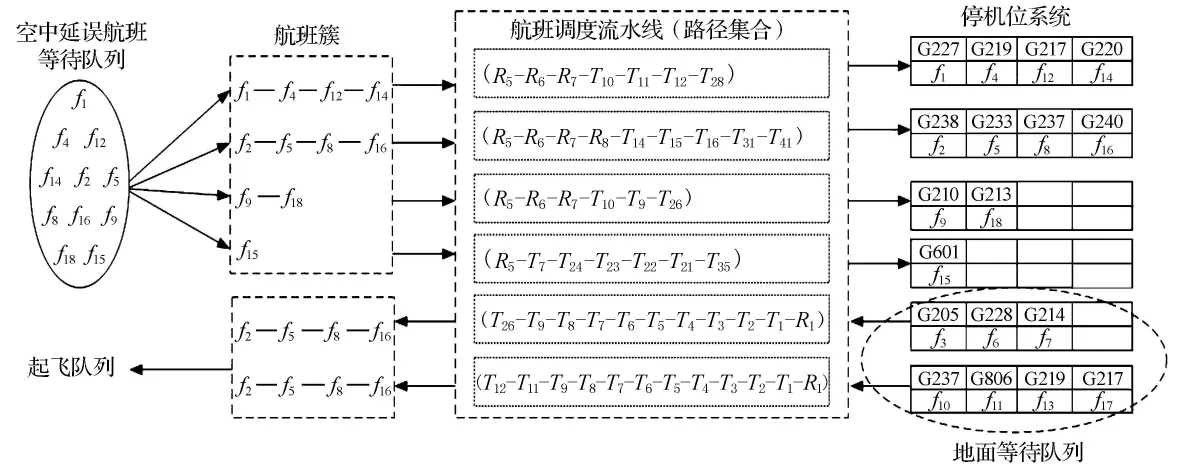
圖3 延誤航班流水調度

求解航班應急調度模型，設置種群數50，最大迭代次數100，慣性因子0.4.同時，根據每組航班簇的航空器數量不同，設置多粒子種群個數，分別為4，4，2，1，3，4組粒子分別計算.依照假設條件中的風險級別規定，待降航班的調度優先級大于起飛航班，調度過程如圖3所示.

從圖4的計算結果看，多粒子群算法不到80代即收斂得到全局最優解.但是，多粒子群算法在計算局部小規模的航班簇調度中，相比FCFS方式總體優勢不明顯，每個局部最優的總和2 501s的總體調度時間效率僅僅提高98s；當將所有延誤航班看成一個整體進行全局流水航班調度時，總體調度時間為1 745s，較之FCFS提高了854s（14.2min），見表3.調度結果，對編排新的調度計劃有非常有意義的參考價值.

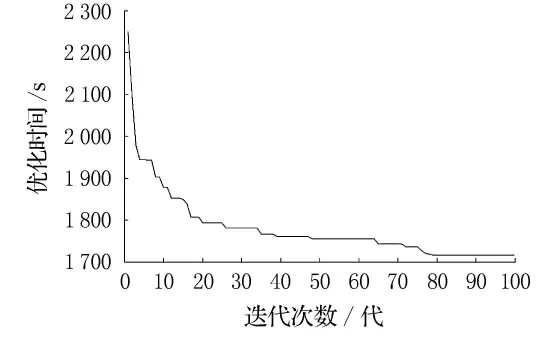
圖4 迭代次數與最優解

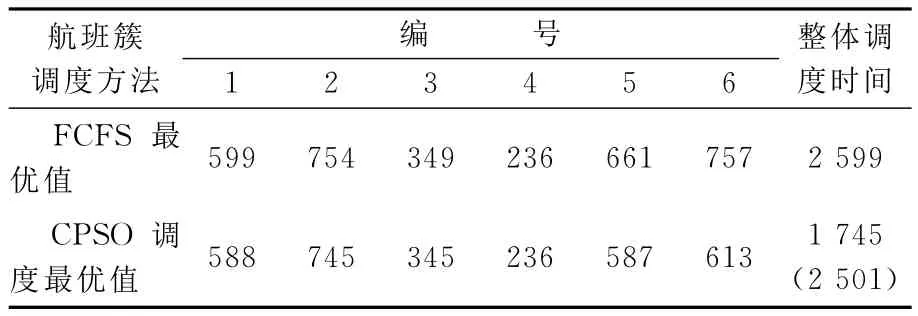
表3 航班調度結果比較 s

5 結 論

1）延誤航班調度問題可以轉化為車間調度中特殊的流水線調度方法，處理延誤航班需要分析和正確歸類有類似屬性的航班計劃，模擬流水車間處理具有相同工序工件的方式.

2）建立的延誤航班應急調度模型可以用來求解不正常航班調度計劃，以此提高機場場面控制部門的調度效率和機場容量.通過適應性改進后可以應用于樞紐機場單跑道場面的延誤航班調度，具有一定的實際參考價值.

3）多粒子群算法在處理大規模復雜優化問題方面具有時間效率和解空間快速收斂的優勢，可以作為此類模型可靠的求解算法之一.

［1］趙文智，王化佳.一個航班備降延誤的成本分析［J］.中國民航大學學報，2009，12（6）：45－47.

［2］CAPOZZI B J，DIFELICI J.Towards automated airport surface traffic control：potential benefits and feasibility［C］／／ AIAA Guidance，Navigation，and Control Conference and Exhibit，2004（8）：1－16.

［3］RATHINAM S，MONTOYA J，JUNG Yoon.An optimization model for reducing aircraft taxi times at the dallas fort worth international airport［C］／／26th International Congress of The Aeronautical Sciences，2008：1－14.

［4］ANAGNOSTAKIS I，CLARKE J P.Runway operations planning：a two－stage solution methodology［C］／／Proc.of the 36th Hawaii International Conference on System Sciences（HICSS′03），2003：1－12.

［5］尤 杰，韓松臣.基于多智能體MAS的智能交通控制系統的研究［J］.交通運輸工程學報，2009，2（1）：109－113.

［6］王艷軍，胡明華，蘇 煒.基于沖突回避的動態滑行路徑算法［J］.西南交通大學學報，2009，12（6）：933－940.

［7］王萬良，周 明，徐新黎，等.基于改進粒子群算法的離子膜車間調度問題研究［J］.控制與決策，2010，25（7）：1021－1025.

［8］李愛國.多粒子群協同優化算法［J］.復旦學報：自然科學版，2004，43（5）：923－925.