關(guān)于抽樣調(diào)查中多層次調(diào)查問題的探討
呂 萍
0 引言
抽樣調(diào)查作為一種獲取統(tǒng)計(jì)資料的重要手段,日益受到政府各部門、企業(yè)、學(xué)術(shù)界和社會(huì)公眾的重視。由于中國各級(jí)政府都要管經(jīng)濟(jì),各級(jí)行政長官都關(guān)心本地區(qū)的經(jīng)濟(jì),都需要掌握有關(guān)統(tǒng)計(jì)數(shù)據(jù),出現(xiàn)了如何滿足多層次調(diào)查的需要,也就是多層次抽樣調(diào)查的問題。此處的層次包含在抽樣設(shè)計(jì)中的為了提高抽樣效率利用輔助信息分的層,也包含行政設(shè)置中的省市、區(qū)縣、村居等的自然層,也稱為域,分層次調(diào)查問題是總體和各個(gè)層次(也稱為域、子總體)都需要估計(jì)的問題。尤其是大型的抽樣調(diào)查,例如中國科學(xué)素養(yǎng)調(diào)查、中國婦女的社會(huì)地位等大型綜合調(diào)查都需要在對(duì)全國的目標(biāo)變量進(jìn)行估計(jì)的基礎(chǔ)上也對(duì)各省(層次)的目標(biāo)變量進(jìn)行估計(jì)。
解決分層次調(diào)查問題的方法主要有直接估計(jì)方法和間接估計(jì)方法。其中直接估計(jì)方法主要有層層抽樣的方法、ABC法[1]、樣本追加法[2]。其中,層層抽樣和ABC三級(jí)[1]一套的樣本設(shè)計(jì)是一種自下而上的抽樣思路,簡(jiǎn)單直接,但由于需要對(duì)所有的縣都進(jìn)行調(diào)查,經(jīng)費(fèi)龐大從而違背了抽樣調(diào)查的經(jīng)濟(jì)性的優(yōu)勢(shì),而且各個(gè)縣的工作效率以及調(diào)查和估計(jì)很難統(tǒng)一等缺點(diǎn),在實(shí)際應(yīng)用中有很大的局限性。樣本追加方法是一種自下而上抽樣設(shè)計(jì)思路,是由馮世雍與秦懷振[3]于2002年提出的一種分層次抽樣設(shè)計(jì)方法,是在滿足上一級(jí)目標(biāo)變量估計(jì)精度需要的基礎(chǔ)上用樣本追加的方法來滿足下一級(jí)尤其是省級(jí)目標(biāo)變量估計(jì)精度的需要。間接估計(jì)方法是充分挖掘已有的樣本信息,充分利用間接信息和數(shù)據(jù)改進(jìn)各個(gè)層次的目標(biāo)變量的估計(jì)量,與傳統(tǒng)數(shù)理統(tǒng)計(jì)中的時(shí)間序列、回歸模型、貝葉斯統(tǒng)計(jì)等方法得到各個(gè)層次的目標(biāo)變量的有效估計(jì)量。
1 分層次調(diào)查的抽樣設(shè)計(jì)思路
在實(shí)踐中主要有兩種多層次調(diào)查問題。第一,總體和各層次的調(diào)查不同時(shí)進(jìn)行,即總體調(diào)查在前,省級(jí)調(diào)查在后。第二,總體與省級(jí)調(diào)查總體的調(diào)查同時(shí)進(jìn)行。從抽樣設(shè)計(jì)的角度,有兩種解決上述分層次調(diào)查問題的樣本追加方法,一種是用馮世雍與秦懷振于2002年提出的樣本追加方法,一種是利用永久隨機(jī)數(shù)的方法來進(jìn)行樣本追加。
1.1 分層次調(diào)查中的樣本追加方法
樣本追加方法的基本思想是按照某種特定的概率抽樣方法,從總體中抽取樣本對(duì)總體的目標(biāo)變量進(jìn)行估計(jì)。但對(duì)于其中的某些層或域,由于落入該層的樣本單元不能保證對(duì)該層或域的目標(biāo)量推斷的需要,即落入其中的樣本對(duì)該層或域沒有代表性,此時(shí)在該層內(nèi)按照某種抽樣方法追加部分樣本單元與原來落入該層或域的樣本(主體樣本)組成復(fù)合樣本來對(duì)該層的目標(biāo)量進(jìn)行推斷,通過樣本追加滿足來下一層目標(biāo)量估計(jì)的需要,兩級(jí)樣本相互兼容,同時(shí)利用這些追加的樣本還可以進(jìn)一步提高總體目標(biāo)量的估計(jì)精度。
這種方法的優(yōu)勢(shì)主要體現(xiàn)在:(1)樣本追加可以很好地實(shí)現(xiàn)多級(jí)樣本的兼容,以提高樣本的使用效率,節(jié)約調(diào)查成本;(2)樣本追加避免各個(gè)層都要抽樣帶來的人力物力財(cái)力的浪費(fèi),只在有推斷要求的層追加樣本。(3)樣本追加可以進(jìn)一步提高上級(jí)目標(biāo)變量的估計(jì)精度。
多層次調(diào)查中的樣本追加將抽樣設(shè)計(jì)分為主體設(shè)計(jì),追加設(shè)計(jì)和終極設(shè)計(jì)。為確保總體推斷的可靠性而制定的抽樣設(shè)計(jì)稱為主體設(shè)計(jì),為確保對(duì)某種層推斷的可靠性而為需要追加層制定的抽樣設(shè)計(jì)稱為域追加設(shè)計(jì)。主體設(shè)計(jì)和追加設(shè)計(jì)連同實(shí)施方案一起的抽樣設(shè)計(jì)稱為終極設(shè)計(jì)。
當(dāng)總體的抽樣設(shè)計(jì)與層的追加設(shè)計(jì)獨(dú)立進(jìn)行、獨(dú)立實(shí)施,利用終極樣本對(duì)總體以及需要估計(jì)的層(層)的目標(biāo)變量進(jìn)行估計(jì)的樣本追加方法稱為獨(dú)立樣本追加方法。在實(shí)施主體設(shè)計(jì)的基礎(chǔ)上在層進(jìn)行樣本追加,對(duì)總體以及層的目標(biāo)變量的估計(jì)稱為條件樣本追加。不管是獨(dú)立追加設(shè)計(jì)還是條件追加設(shè)計(jì),其基本的設(shè)計(jì)思想是根據(jù)主體的抽樣設(shè)計(jì)和層的樣本追加設(shè)計(jì)分別構(gòu)造總體和層的參數(shù)估計(jì)并選擇合適的方差估計(jì)方法;然后構(gòu)造總體和層參數(shù)的估計(jì)類,在類內(nèi)選擇最優(yōu)偽估計(jì),構(gòu)造漸進(jìn)局部最優(yōu)估計(jì),從而得到層的目標(biāo)變量的最優(yōu)估計(jì)量。
在實(shí)際調(diào)查中,獨(dú)立樣本追加是易于操作的樣本追加方法,只需將主體設(shè)計(jì)和層的追加設(shè)計(jì)按照各自的抽樣方案獨(dú)立設(shè)計(jì)、獨(dú)立進(jìn)行、獨(dú)立設(shè)施,相當(dāng)于做了兩次獨(dú)立的抽樣調(diào)查,然后利用極小化方差的思想,在主體設(shè)計(jì)與追加設(shè)計(jì)都可測(cè)并滿足最小方差的前提下,基于主體樣本和追加樣本分別構(gòu)造總體的目標(biāo)變量的H-T估計(jì)量及其方差估計(jì)量,最后利用極小方差的方法在層的線性無偏類中找到目標(biāo)變量的最優(yōu)估計(jì)量。以總量估計(jì)為例,利用總體總量Y的H-T估計(jì)Y?π和層的總量YD的H-T估計(jì)Y?Dπ及其方差估計(jì)量,層追加樣本的總量估計(jì)量Y?+Dπ及其方差的無偏估計(jì)量;然后通過極小化方差的方法在YD的線性無偏類 {Y?D(θ)=θY?Dπ+(1-θ)Y?Dπ+;θ∈R}里找到局部最優(yōu)偽估計(jì);最后通過估計(jì)其方差里的未知系數(shù)來構(gòu)造層總量的漸進(jìn)局部最優(yōu)估計(jì)。
由上得到
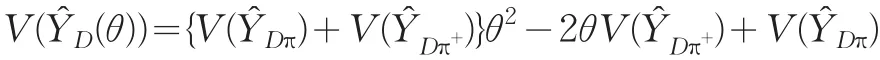

得到獨(dú)立追加在追加設(shè)計(jì)可測(cè)的情況下,層的估計(jì)量Y?D(θ)的最有方差估計(jì)量是
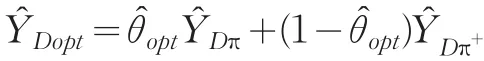
可以驗(yàn)證當(dāng) Cov(θ?opt,Y?Dπ-Y?Dπ+)→ 0 時(shí),Y?Dopt是YD的漸進(jìn)無偏估計(jì)量。
利用獨(dú)立樣本追加設(shè)計(jì)還可以對(duì)總體的估計(jì)量進(jìn)行改進(jìn),設(shè)C=UD為剩余層,則剩余層YC=Y-YD的基于主體設(shè)計(jì)的目標(biāo)變量的H-T估計(jì)量Y?Cπ=Y?π-Y?Dπ,可以得到終極設(shè)計(jì)下的總體總量 Y 的估計(jì) Y?bet(θ?opt)=Y?Cπ+Y?opt,可以驗(yàn)證Y的H-T估計(jì)量和最優(yōu)方差加權(quán)估計(jì)量 Y?(θ?opt)都是無偏的。由此,構(gòu)造總量Y?π的無偏估計(jì)類Y? ={Y?(α|θopt)= αYπ+(1- α)Y?bet(θ?opt),α ∈ R},利用極小化方差V(α|θopt)求得最優(yōu)點(diǎn) αopt(θopt),可得出
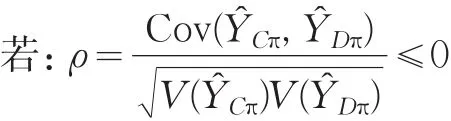
由此得到Y(jié)?π的最優(yōu)估計(jì)量是 αoptYπ+(1-αopt)Y?bet(θ?opt)。
1.2 利用永久隨機(jī)數(shù)進(jìn)行的分層次抽樣設(shè)計(jì)
上述樣本追加方法都需要進(jìn)行二次抽樣,有時(shí)會(huì)導(dǎo)致樣本單元的過量抽取和使用,利用永久隨機(jī)數(shù)技術(shù)可以有效處理樣本追加問題。永久隨機(jī)數(shù)技術(shù),即抽樣框中的每個(gè)單元都被賦予從區(qū)間(0,1)產(chǎn)生的隨機(jī)數(shù),永久隨機(jī)數(shù)和這個(gè)單元同時(shí)產(chǎn)生,同時(shí)改變,同時(shí)消亡。永久隨機(jī)數(shù)技術(shù)實(shí)施起來非常方便,可以有效地解決多目標(biāo)、分層次、與規(guī)模成比例的不等概抽樣調(diào)查以及實(shí)現(xiàn)連續(xù)調(diào)查中的樣本輪換等問題。將永久隨機(jī)數(shù)技術(shù)和樣本追加方法結(jié)合起來,可以有效地解決分層次調(diào)查中的樣本兼容問題,方便的實(shí)現(xiàn)樣本追加,使抽到的樣本對(duì)總體有更好的代表性。抽樣方法按照樣本量是否固定分為兩類,隨機(jī)樣本量和固定樣本量的抽樣方法。隨機(jī)樣本量的抽樣方法有Poisson抽樣、Bernoulli抽樣、配置抽樣、PoMix抽樣和Mpps抽樣,其中以Poisson抽樣為代表。固定樣本量的抽樣方法有序貫Srswor抽樣、序貫Poisson抽樣、Pareto抽樣和序貫PoMix抽樣,其中以序貫Poisson抽樣為代表。
利用永久隨機(jī)數(shù)抽樣技術(shù)可以方便地解決實(shí)際調(diào)查中存在的總體與層調(diào)查同時(shí)進(jìn)行以及總體調(diào)查與層調(diào)查不同時(shí)進(jìn)行的分層次抽樣調(diào)查。
2 總體調(diào)查與各層調(diào)查同時(shí)進(jìn)行
利用永久隨機(jī)數(shù)法的分層次調(diào)查是對(duì)總體中每一個(gè)單位賦予永久隨機(jī)數(shù),確定樣本的排列順序,使各層次的樣本能有較高的兼容共享性,也避免了二次抽樣和樣本重復(fù)抽樣的情況。針對(duì)分層次調(diào)查中總體和層同時(shí)抽樣的情況,即其中層與總體同時(shí)進(jìn)行調(diào)查,此時(shí)只需對(duì)層進(jìn)行調(diào)查,總體樣本的數(shù)據(jù)也就能夠從層中獲得。此處我們利用永久隨機(jī)數(shù)抽樣法中隨機(jī)樣本量的Poisson抽樣方法或固定樣本量的序貫Poisson抽樣方法來處理,因?yàn)镻oisson抽樣法是一種與規(guī)模成比例的不等概抽樣方法,更符合實(shí)踐中復(fù)雜抽樣的設(shè)計(jì)。其中Poisson抽樣法由于樣本量的隨機(jī)性,最終實(shí)現(xiàn)的樣本量與期望的樣本量有一定的差異,可以通過永久隨機(jī)數(shù)的修勻來減少隨機(jī)樣本量的變動(dòng)情況。下面介紹總體與層調(diào)查同時(shí)進(jìn)行的兩階段分層次調(diào)查。
將總體的每一個(gè)單元賦予永久隨機(jī)數(shù),并將總體U劃分為M個(gè)層,其中若干個(gè)層和總體同時(shí)進(jìn)行估計(jì),不失一般性,假設(shè)U1,U2,...Ur和U同時(shí)調(diào)查,總體的樣本容量為n。
(1)當(dāng)r=M時(shí),即所有的層都與總體同時(shí)調(diào)查,利用永久隨機(jī)數(shù)法,只需要對(duì)U1,U2,...Ur進(jìn)行調(diào)查即可,因此首先在U1,U2,...Ur中分別利用永久隨機(jī)數(shù)得到U1,U2,...Ur各自的樣本,由永久隨機(jī)數(shù)法的性質(zhì)可知總體的樣本一定在U1,U2,...Ur樣本的并集中,此時(shí)只需在U1,U2,...Ur樣本的并集中,按照總體樣本的排列順序選定前n個(gè)單元就可,因此無需再抽樣就可以完成總體和各層的抽樣。
(2)當(dāng)r<M 時(shí),將U 劃分為兩個(gè)子集U(1)和U(2),樣本量分別為n1和n2。
在(2)中,若事先已知總體U 的兩個(gè)子集U(1)和U(2)的樣本量為n1和n2,則由永久隨機(jī)數(shù)的性質(zhì),則兩部分的樣本之和即為總體中隨機(jī)數(shù)最小的n個(gè)永久隨機(jī)數(shù)對(duì)應(yīng)的單元,為總體的樣本。若事先不知道總體U的兩個(gè)子集U(1)和U(2)的樣本量為n1和n2,則首先按照(1)的方法在U(1)中選取永久隨機(jī)數(shù)最小的n個(gè)單元作為總體U的樣本,然后與U(2)中的單元的永久隨機(jī)數(shù)進(jìn)行比較,如果對(duì)應(yīng)的永久隨機(jī)數(shù)小于U(1)中的n個(gè)樣本單元對(duì)應(yīng)的永久隨機(jī)數(shù),則將Ui(2)迭代進(jìn)入樣本,將U(1)中的最大的那個(gè)隨機(jī)數(shù)迭代出來,以此方式迭代下去,即得到總體U的n個(gè)樣本單元。
多階段的分層次抽樣其方法是類似的,只考慮需要估計(jì)的層和其下的一個(gè)層次,視為兩階段的分層次抽樣調(diào)查即可。
3 總體調(diào)查與層調(diào)查不同時(shí)進(jìn)行
當(dāng)總體調(diào)查與層調(diào)查不同時(shí)進(jìn)行時(shí),同樣對(duì)總體中的每一個(gè)單元賦予永久隨機(jī)數(shù),具體實(shí)施思路如下,仍以兩階段的分層次調(diào)查為例。假設(shè)第一次對(duì)總體進(jìn)行調(diào)查時(shí)此層的樣本量為n1,由于此樣本對(duì)于該層缺乏代表性,所以需要進(jìn)行第二次抽樣調(diào)查,即對(duì)該層進(jìn)行樣本追加,若追加的樣本量為n2,利用永久隨機(jī)數(shù)方法只需在選擇n1個(gè)永久隨機(jī)數(shù)對(duì)應(yīng)的樣本的基礎(chǔ)上再選擇n2最小永久隨機(jī)數(shù)對(duì)應(yīng)的樣本單位即可,大于兩層的多層次調(diào)查的方法類似。
4 利用永久隨機(jī)數(shù)法的參數(shù)估計(jì)
通過上述分析,可以看到永久隨機(jī)數(shù)方法有效地解決了各個(gè)層次的調(diào)查的樣本兼容問題,很好地解決了多層次調(diào)查的樣本的抽取問題,但是從抽樣框中抽取樣本不是抽樣調(diào)查的目標(biāo),而是如何有效地對(duì)總體進(jìn)行有一定精度的估計(jì)。
分層次抽樣調(diào)查中的永久隨機(jī)數(shù)抽樣方法,一般是Poisson或序貫Poisson抽樣方法。此處我們應(yīng)用在Poisson抽樣中利用廣義回歸估計(jì)量計(jì)算目標(biāo)變量的無偏估計(jì)量,得到層的估計(jì)量是
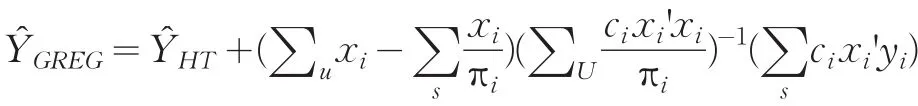
運(yùn)用復(fù)雜方差的棄一的Jackknife方差估計(jì)方法,得到方法估計(jì)量
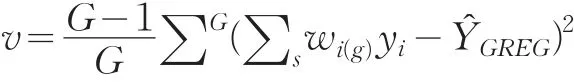
其中
隨機(jī)組的劃分是Jackknife方法的關(guān)鍵,隨機(jī)組的具體劃分要取決于調(diào)查的具體抽樣設(shè)計(jì)。
5 總結(jié)
文章主要針對(duì)實(shí)際調(diào)查中的分層次調(diào)查問題展開討論,現(xiàn)在許多大型的調(diào)查都需要在對(duì)總體的目標(biāo)變量進(jìn)行估計(jì)的基礎(chǔ)對(duì)各個(gè)層次也進(jìn)行有效的估計(jì)。本文主要介紹了馮世雍與秦懷振的樣本追加方法和利用永久隨機(jī)數(shù)的樣本追加方法。
[1]秦懷振.抽樣調(diào)查中若干理論與實(shí)踐問題的研究[M].北京:中國統(tǒng)計(jì)出版社,2003.
[2]Rao,J.N.K.Small Area Estimation[M].New York:Wiley,2003.
[3]馮士雍.中國抽樣調(diào)查應(yīng)用中的若干問題[J].中國統(tǒng)計(jì),2001,(11).
[4]林才生.分層次復(fù)合pps抽樣設(shè)計(jì)[J].統(tǒng)計(jì)與決策,2006,(13)

