移動機器人復雜路徑規劃優化方法研究

張德惠， 王利輝

ZHANG De-hui1, WANG Li-hui2

（1. 內蒙古民族大學 機械工程學院，通遼 028000；2.長春理工大學 機電工程學院，長春130022）

0 引言

移動機器人面對復雜路徑時，需要進行路徑識別與決策。如何能夠快速完成對復雜環境的分析，并作出正確決策，是移動機器人程序設計中的一個重要環節。機器人路徑規劃問題，可分為環境參數可知的路徑規劃和環境參數未知的路徑規劃。環境可知的路徑規劃即路徑尋優問題，能實現快速避障以及全局路徑最短等目的[1]，全局路徑規劃方法采用可視圖法、圖搜索法、人工勢場法等[2]。環境未知的路徑規劃主要通過安裝在機器人身上的眾多傳感器，利用傳感器融合技術采集環境參數，對機器人的行動進行判斷。人工神經網絡的發展以及支持向量機的興起，使得對環境參數的判斷成為了系統辨識理論新的研究對象。

環境可知的路徑規劃研究中，以往的研究方法集中在路徑搜索問題上，如文獻[3]研究的改進型遺傳算法，文獻[4]所提出的神經網絡快速優化算法，都旨在從理論本身上消除或者減小該理論所帶來的缺陷，從而保證算法的實現。文獻[5,6]用新的方法來克服人工勢場方法在機器人路徑規劃方面的不足[7]。

本文針對移動機器人路徑尋優過程中所得復雜軌跡特點，通過坐標變換，選擇合適的坐標原點與坐標系，得到適合神經網絡優化處理的點集，快速有效準確的對路徑規劃后的軌跡進行優化處理。

1 復雜路徑規劃優化方法

在對機器人路徑規劃研究過程中，筆者發現對于不同的路徑規劃，會得到不同的優化效果。規劃路徑的多點重合、多周迂回、部分路段重合等因素，增加了規劃路徑的復雜度，使通過神經網絡或n次多項式擬合得到的全局優化結果很難接近真實值，甚至出現擬合曲線回歸原點等崩潰現象。如何防止這些現象的發生，除了引言部分提到的，將智能算法與其他理論結合以外，還可以根據路徑的特點，選擇適當的坐標原點并做合理的坐標變換，讓很難處理的復雜路徑變得容易處理，這樣，可以簡化路徑規劃中得算法優化問題，從而降低了理論模型的計算量。

1.1 坐標平移變換方法

針對計算機生成的復雜路徑，為便于神經網絡做后續優化處理，提出該方法。該方法主要通過對坐標原點的平移，將路徑的起始點與終點進行衡量，確定坐標原點，并通過新坐標系，對路徑進行極坐標變換，將原解析坐標系下得路徑映射到極坐標系下，并通過極坐標展開，得到圖形更為簡單的路徑點集。便于神經網絡做后續優化處理。圖1(a)為機器人從起始點到目的地的規劃后路徑，可以看出坐標是隨系統初始位置產生的。下面是具體轉化方法。

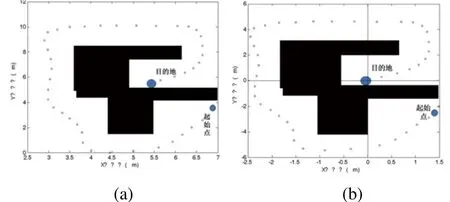
圖1 機器人路徑示意圖

對于這種環繞形的路徑規劃問題，可以把目的地作為整個范圍的中心，得到一個近似于圓的路徑規劃問題。首先進行坐標平移，由圖2可知，初始坐標系下目的地坐標為（x0，y0），變換到新坐標系下，可以得到新坐標系下任意點坐標為：

其中的（x，y）為A點的初始坐標，（x'，y'）為A點平移后的坐標。

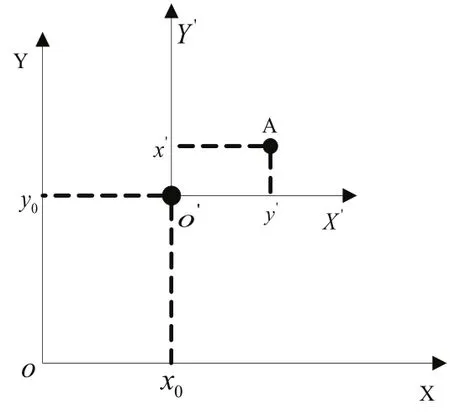
圖2 坐標平移示意圖

坐標平移以后，就得到新坐標系下規劃路徑，如圖1(b)所示。

坐標變換后路徑上的點集位于初始點的周圍，將這些點變換到極坐標下，變換方法如圖3所示：

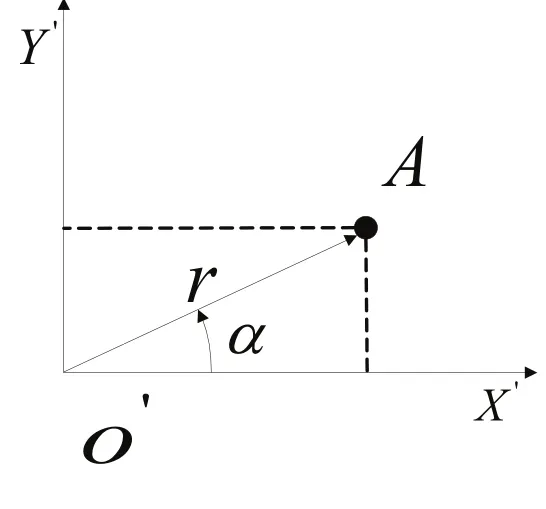
圖3 直角坐標轉極坐標示意圖

變換公式為：

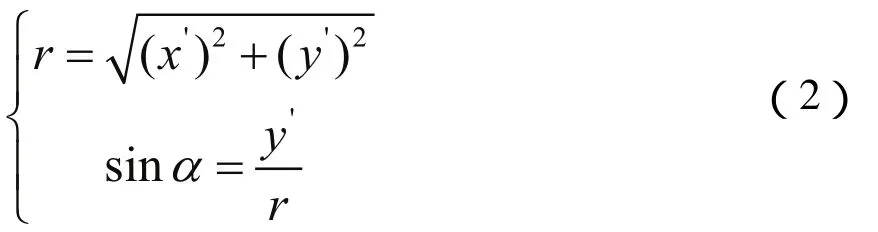
其中，r 為A點的極軸，α為極徑， x'為A點直角坐標系上得很坐標， y'為縱坐標。得到直角坐標系變換到極坐標系下的路徑如圖4所示：

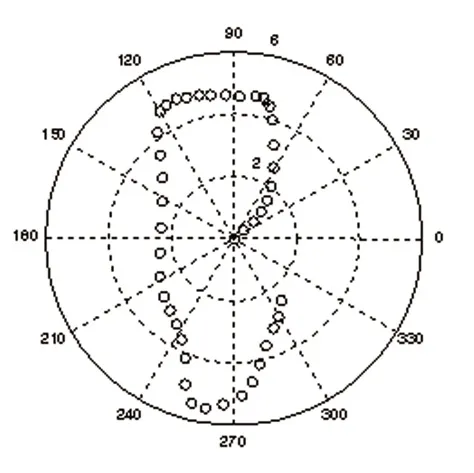
圖4 極坐標下的機器人路徑圖

將此極坐標下得路徑展開在直角坐標系下，有：

得到展開后的軌跡如圖5所示。

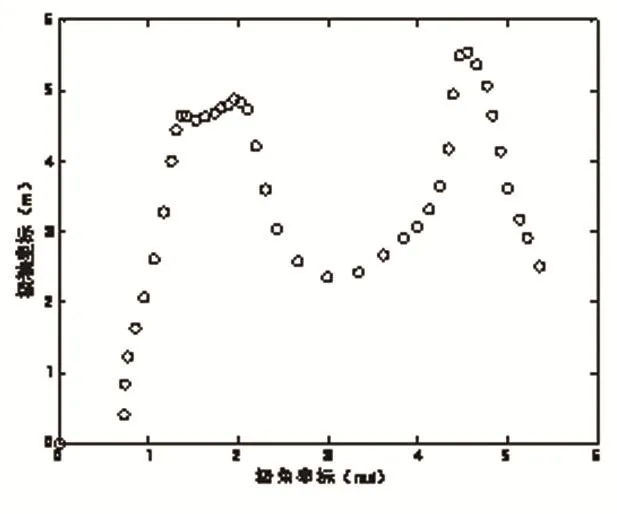
通過一系列變換，得到了在直角坐標系下機器人規劃路徑，從路徑軌跡上看，對比與原路徑軌跡，已經有相當簡化。其表現出來的非線性，需要神經網絡對其進行非線性擬合。通過自學習，并調整逼近精度和神經元數量，能夠達到很好的擬合效果。

進行神經網絡擬合后的曲線，可以利用坐標轉換，轉換成直角坐標系下，即：

利用此方法，得到最終經神經網絡擬合曲線，根據神經網絡的特性，可以充分體現出路徑的非線性。

1.2 神經網絡優化方法

本文利用BP神經網絡對機器人路徑進行優化，即對給出的機器人路徑做非線性擬合。

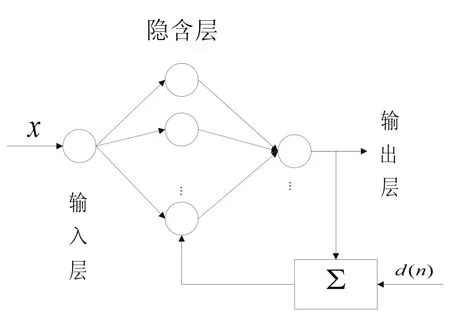
圖6 神經網絡結構示意圖

圖6所示，該神經網絡具有1個輸入，1個輸出和一個隱含層。將展開路徑的橫坐標（極坐標的角度）作為輸入樣本，每一個樣本輸入網絡，進行訓練。

神經元輸出為：

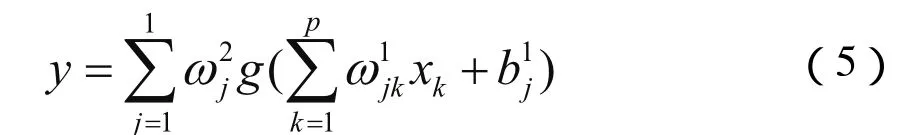
式中，ω2ω1為神經元輸入層和輸出層的權jjk值，P為隱層節點數，b1為閾值。取Sigmoid活化j函數：

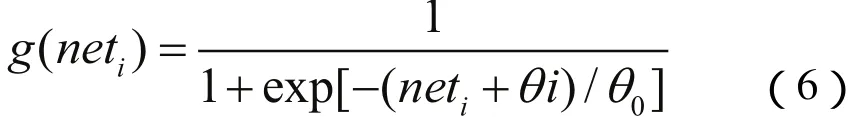
式中，neti為神經網絡各節點輸入，參數θi表示閾值，θ0為函數平緩程度。

神經網絡學習方法為最速梯度下降法，根據最速下降法得到的權值變量，對神經網絡各個節點間的權值進行修改，得到權值變量

其中η為學習速率，η＞0，Ep為引入的二次型誤差函數，與訓練樣本有關，wki為各層權值。

2 實驗及仿真分析

根據路徑規劃過程中分析得到的特征，選取了三種復雜路徑，即實際路徑、李薩如路徑和近似螺旋路徑。其中交叉路徑選用李薩如曲線軌跡，該圖像多次交于原點，軌跡復雜。近似螺旋路徑的特點是具有多圈軌跡，在直角坐標系下很容易引起擬合算法陷入局部最小或擬合曲線回歸原點等現象。

對這三種路徑進行了坐標變換和神經網絡優化，得到仿真對比圖像，具體如圖7～圖9所示。

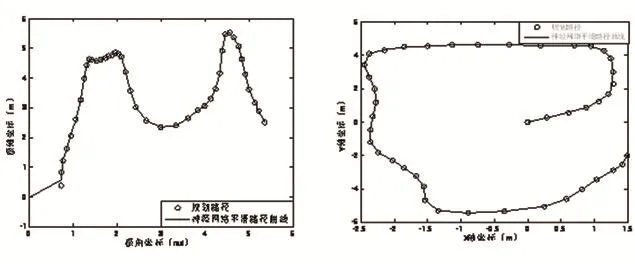
(a) (b)圖7 實際路徑坐標平移轉換仿真優化比較

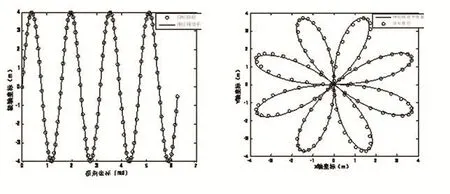
(a) (b)圖8 李薩如路徑坐標平移轉換仿真優化比較

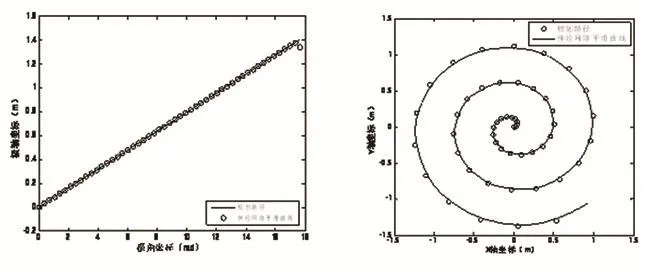
(a) (b)圖9 近似螺旋路徑坐標平移轉換仿真優化比較

圖7(a)、圖8(a)、圖9(a)為在極坐標展開坐標系下，神經網絡擬合曲線與原路徑的對比圖，圖7(b)、圖8(b)、圖9(b)為轉換到直角坐標系下神經網絡擬合曲線與原路徑的對比圖。

3 結論

本文通過對移動機器人復雜路徑特征的分析，提出了一種基于坐標平移變換的神經網絡曲線擬合平滑路徑優化方法，該方法使得復雜的路徑優化問題，在極坐標空間更容易實現。并避免了因路徑復雜帶來的各種智能算法局部最小問題。仿真表明，利用神經網絡進行的路徑優化，訓練穩定，逼近精度高，能夠應用于機器人路徑規劃的優化中去。

[1] Kim W S.Virtual reality calibration for telerobotic servicing[A].Proceedings of the IEEE International Conference on Robotics and Automation[C].Piscataway,NJ,USA: IEEE,1994.2769 -2775.

[2] Staudte R G,Sheather S J,Robust Estimation and Testing.Wi-ley,New York,1990.

[3] 仲欣,呂恬生.基于遺傳算法的汽車式移動機器人路徑規劃方法[J],上海交通大學學報,1999,33(7):885-888.

[4] 禹建麗,V.Kroumov.一種快速神經網絡路徑規劃算法[J],機器人,2001.(3):201-205.

[5] 曲道奎,杜振軍,移動機器人路徑規劃方法研究,機器人[J],2008.(2):97-106.

[6] 于振中,閆繼宏,趙杰,陳志峰,朱延河.改進人工勢場法的移動機器人路徑規劃[J],哈爾濱工業大學學報,2011.43(1):50-54.

[7] Han J D, Mark Campbell. Arti fi cial potential guided evolutionary path plan for target pursuit and obstacle avoidance[J].In:2003 AIAA Guidance, Navigation and Control Conference and Exhibit Austin, TX. August 2003.