基于最小歐式距離(1+1)小生境遺傳算法的無(wú)功優(yōu)化
鄧艷秋,滿小平,繩環(huán)宇,韓學(xué)軍
(1.東北電力大學(xué)電氣工程學(xué)院,吉林吉林132012;2.通化供電公司變電工區(qū),吉林通化134000)
0 引言
電力系統(tǒng)無(wú)功優(yōu)化是通過(guò)對(duì)發(fā)電機(jī)端電壓、可調(diào)變壓器分接頭和無(wú)功補(bǔ)償設(shè)備的綜合調(diào)節(jié),使系統(tǒng)滿足運(yùn)行電壓、有載調(diào)壓變壓器的分接頭檔位和無(wú)功補(bǔ)償設(shè)備投入以及發(fā)電機(jī)的安全運(yùn)行等約束條件,并使有功損耗最小及母線電壓偏移量在合格范圍內(nèi)。無(wú)功優(yōu)化的算法很多,但都存在不足,梯度法、內(nèi)點(diǎn)法、線性規(guī)劃和非線性規(guī)劃等常規(guī)優(yōu)化算法要求目標(biāo)函數(shù)可微、對(duì)初值要求高、求解時(shí)間較長(zhǎng)和容易產(chǎn)生維數(shù)災(zāi)等缺點(diǎn)[1]。現(xiàn)代啟發(fā)式算法有遺傳算法(genetic algorithm,GA)、模擬退火算法、粒子群算法和禁忌搜索法[2-7]等,容易出現(xiàn)早熟現(xiàn)象和陷入局部收斂等不足之處,其各種改進(jìn)形式主要是提高全局尋優(yōu)能力和加快收斂速度。因此,遺傳算法[9]因?qū)η蠼庑畔⒁笊佟⒔:?jiǎn)單、適用范圍廣和尋優(yōu)能力強(qiáng)等優(yōu)點(diǎn)而被廣泛應(yīng)用。
小生境遺傳算法具有很高的全局尋優(yōu)能力和收斂速度,在保持解的多樣性方面表現(xiàn)優(yōu)異,但是小生境參數(shù)設(shè)定的不同對(duì)算法進(jìn)化影響極大,這些參數(shù)的設(shè)定要有事先的預(yù)見(jiàn)性和參考性,用經(jīng)驗(yàn)選取參數(shù)的方法,會(huì)影響這類算法的優(yōu)勢(shì)。因此,本文將一種全新的小生境遺傳算法(1+1)GA[8]應(yīng)用于無(wú)功優(yōu)化問(wèn)題中,并結(jié)合無(wú)功優(yōu)化的特點(diǎn)在遺傳算子、終止原則等方面進(jìn)行了改進(jìn)。
1 無(wú)功優(yōu)化的數(shù)學(xué)模型
電力系統(tǒng)無(wú)功優(yōu)化問(wèn)題的基本數(shù)學(xué)模型包括目標(biāo)函數(shù)、功率方程約束和變量約束條件。
1.1 目標(biāo)函數(shù)
電力系統(tǒng)無(wú)功優(yōu)化控制是系統(tǒng)在滿足各種運(yùn)行約束條件下,通過(guò)對(duì)發(fā)電機(jī)自動(dòng)電壓調(diào)節(jié)器(au-tomatic voltage regulator,AVR)、有載變壓器分接頭和無(wú)功補(bǔ)償裝置的綜合調(diào)節(jié),使得系統(tǒng)有功損耗、電壓分布與期望值的差值、控制代價(jià)或者它們的任意組合等最小。本文以有功損耗最小為控制目標(biāo),綜合考慮系統(tǒng)節(jié)點(diǎn)電壓和發(fā)電機(jī)無(wú)功出現(xiàn)越界情況,以罰函數(shù)的形式構(gòu)造的目標(biāo)函數(shù)為
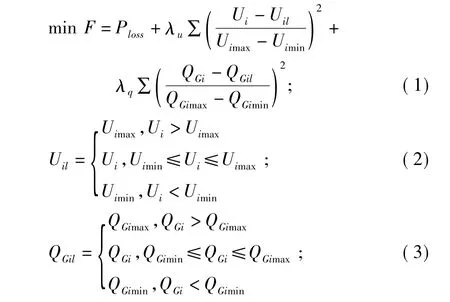
式中:Ploss為系統(tǒng)有功損耗;式(1)的第(2)項(xiàng)為對(duì)負(fù)荷節(jié)點(diǎn)電壓越界的懲罰項(xiàng);式(1)的第(3)項(xiàng)為對(duì)發(fā)電機(jī)無(wú)功越界的懲罰項(xiàng);λu為電壓越界罰系數(shù);λq為發(fā)電機(jī)無(wú)功越界罰系數(shù);Ui、QGi分別為負(fù)荷節(jié)點(diǎn)電壓和發(fā)電機(jī)無(wú)功功率;Uimax、Uimin和QGimax、QGimin分別為對(duì)應(yīng)變量的上下限。
1.2 功率方程約束
在無(wú)功優(yōu)化模型中,考慮節(jié)點(diǎn)有功和無(wú)功功率平衡約束,即
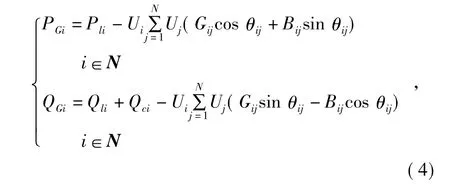
式中:PGi、QGi分別為發(fā)電機(jī)節(jié)點(diǎn)的有功功率和無(wú)功功率出力;Pli、Qli分別為負(fù)荷節(jié)點(diǎn)的有功和無(wú)功功率;Gij、Bij和 θij分別為節(jié)點(diǎn) i,j之間的電導(dǎo)、電納和電壓相角差;N為總節(jié)點(diǎn)數(shù)。
1.3 變量約束
變量約束可分為控制變量約束和狀態(tài)變量約束。分接頭可調(diào)變壓器變比K、無(wú)功補(bǔ)償電納B和發(fā)電機(jī)機(jī)端電壓UG為控制變量;節(jié)點(diǎn)電壓U和發(fā)電機(jī)注入無(wú)功QG為狀態(tài)變量。
控制變量的不等式約束為
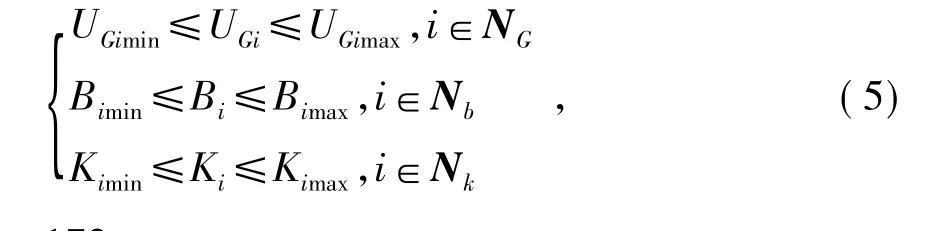
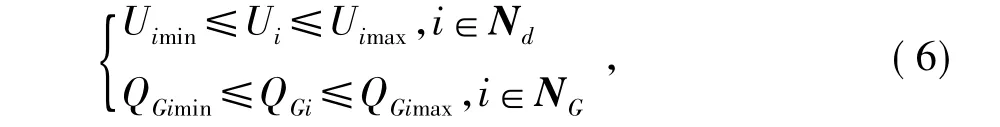
式中:Uimax、Uimin分別為節(jié)點(diǎn)電壓的上下限;QGimax、QGimin分別為發(fā)電機(jī)無(wú)功輸出的上下限;Nd為負(fù)荷節(jié)點(diǎn)數(shù)。式中:UGimax、UGimin分別為發(fā)電機(jī)機(jī)端電壓的上下限;Bimax、Bimin分別為無(wú)功補(bǔ)償電納的上下限;Kimax、Kimin分別為變壓器變比的上下限;NG、Nb、Nk分別為系統(tǒng)發(fā)電機(jī)節(jié)點(diǎn)數(shù)、無(wú)功補(bǔ)償數(shù)、有載變壓器數(shù)。
狀態(tài)變量的不等式約束為
2 最小歐式距離(1+1)小生境遺傳算法
2.1 小生境技術(shù)
小生境技術(shù)是將每一代個(gè)體劃分為若干類,在每個(gè)類中選出若干適應(yīng)度較大的個(gè)體作為一個(gè)類的優(yōu)秀代表組成一個(gè)種群,再將不同種群進(jìn)行雜交、變異,產(chǎn)生新一代個(gè)體種群,同時(shí)采用預(yù)選擇機(jī)制和排擠機(jī)制或分享機(jī)制完成任務(wù)。
2.2 最小歐式距離(1+1)競(jìng)爭(zhēng)小生境遺傳算法
該方法首先將初始種群個(gè)體按順序以歐氏距離計(jì)算法在當(dāng)前種群中找到離其最近的個(gè)體,組成一對(duì),也就是說(shuō)從初始種群中提取一個(gè)個(gè)體A,然后再?gòu)闹姓业狡鋵?duì)應(yīng)的一個(gè)個(gè)體B,由(1+1)個(gè)個(gè)體組成一對(duì),之后的進(jìn)化操作主要是對(duì)每對(duì)個(gè)體進(jìn)行的。如果初始種群個(gè)體為n(n為偶數(shù))個(gè),那么我們能夠組成n/2對(duì)個(gè)體群。分別對(duì)n/2對(duì)個(gè)體中的每對(duì)個(gè)體進(jìn)行交叉、變異操作,交叉采用數(shù)學(xué)交叉,交叉后產(chǎn)生的兩個(gè)子代個(gè)體與兩個(gè)父代個(gè)體合并,根據(jù)適應(yīng)度的大小進(jìn)行競(jìng)爭(zhēng),保留兩個(gè)適應(yīng)度較高的個(gè)體。每對(duì)個(gè)體交叉競(jìng)爭(zhēng)后,所選出個(gè)體重新進(jìn)行最小歐氏距離下的個(gè)體配對(duì)。對(duì)重新配對(duì)后的每?jī)蓚€(gè)個(gè)體,在規(guī)定變異范圍內(nèi)對(duì)每對(duì)個(gè)體進(jìn)行變異。變異后的子代個(gè)體與父代個(gè)體合并,根據(jù)適應(yīng)度大小進(jìn)行競(jìng)爭(zhēng),最終保留兩個(gè)適應(yīng)度較高的個(gè)體。最后對(duì)種群整體進(jìn)行動(dòng)態(tài)交叉、變異操作,到此算法完成了一代進(jìn)化。
算法的流程:
1)產(chǎn)生初始種群,個(gè)數(shù)為n(n為偶數(shù))個(gè)。
2)按照最小歐氏距離法則進(jìn)行個(gè)體配對(duì),形成(1+1)競(jìng)爭(zhēng)模式,組成n/2對(duì)個(gè)體。
3)分別對(duì)n/2對(duì)個(gè)體進(jìn)行交叉,交叉后的兩個(gè)子代個(gè)體與兩個(gè)父代個(gè)體合并進(jìn)行競(jìng)爭(zhēng)排擠,保留較優(yōu)一對(duì)。
4)利用步驟2的配對(duì)規(guī)則,對(duì)個(gè)體重新配對(duì)。
5)分別對(duì)n/2對(duì)個(gè)體進(jìn)行變異,變異后的操作同3)中交叉后的操作。
6)對(duì)整個(gè)群體進(jìn)行交叉,變異操作。
7)判斷程序運(yùn)行是否結(jié)束,如果結(jié)束,輸出當(dāng)前所有個(gè)體。否則,轉(zhuǎn)入第2)步。
3 (1+1)NicheGA在無(wú)功優(yōu)化中的應(yīng)用
為提高最小歐式距離(1+1)競(jìng)爭(zhēng)小生境遺傳算法的收斂速度和計(jì)算速度,考慮電力系統(tǒng)無(wú)功優(yōu)化的實(shí)際情況,對(duì)該算法應(yīng)進(jìn)行進(jìn)一步完善。
1)針對(duì)大規(guī)模電力系統(tǒng)控制變量多的特點(diǎn),采用浮點(diǎn)編碼和整數(shù)編碼相結(jié)合的混合編碼方式,對(duì)發(fā)電機(jī)機(jī)端電壓采用浮點(diǎn)編碼,有載變壓器分接頭和無(wú)功補(bǔ)償容量采用整數(shù)編碼。
2)交叉運(yùn)算采用自適應(yīng)的交叉率,使得適應(yīng)度高的個(gè)體采用較小的交叉率,適應(yīng)度低的個(gè)體采用較高的交叉率,即有
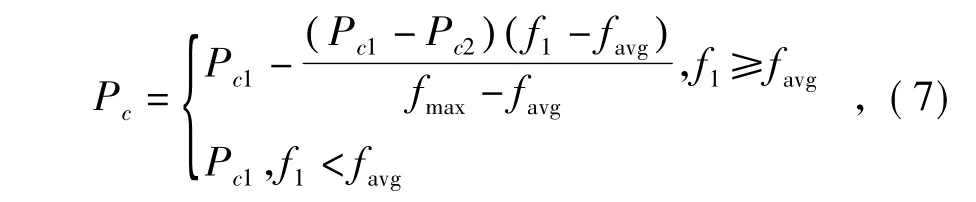
式中:fmax為種群中最大的適應(yīng)度值;favg為每代種群的平均適應(yīng)度值;f1為要交叉的2個(gè)個(gè)體中較大的適應(yīng)度值;Pc1、Pc2為交叉率,0 <Pc2<Pc1<1。變異運(yùn)算采用自適應(yīng)的變異率,將式(7)中的Pc1、Pc2分別替換為 Pm1、Pm2(Pm1、Pm2為變異率,0 < Pm2< Pm1<1),即得到自適應(yīng)的變異率。
3)基于小生境進(jìn)化的一些特點(diǎn),對(duì)整體的交叉、變異不采用恒定不變的方式,即在進(jìn)化的前期,進(jìn)行整體的動(dòng)態(tài)交叉和變異;而在后期,停止整體的交叉、變異操作。這樣,既能保持種群的多樣性又能提高算法的計(jì)算速度和收斂速度。
4)若連續(xù)10代所求解不變,則程序運(yùn)行結(jié)束。(1+1)GA求解無(wú)功優(yōu)化問(wèn)題步驟如圖1所示。
4 算例分析
本文以IEEE30節(jié)點(diǎn)系統(tǒng)作為測(cè)試算例,并將簡(jiǎn)單遺傳算法(SGA)和小生境遺傳算法(NicheGA)進(jìn)行比較,對(duì)所提出的算法進(jìn)行驗(yàn)證。IEEE30節(jié)點(diǎn)算例系統(tǒng)共有6個(gè)發(fā)電機(jī)節(jié)點(diǎn)、22個(gè)負(fù)荷節(jié)點(diǎn)和41條支路。系統(tǒng)中發(fā)電機(jī)的節(jié)點(diǎn)編號(hào)為1、2、5、8、11、13;可調(diào)變壓器支路為6-9、6-10、4-12、27-28;節(jié)點(diǎn)17、18、23、27裝有可投切容性無(wú)功補(bǔ)償設(shè)備。節(jié)點(diǎn)1為平衡節(jié)點(diǎn),余下的發(fā)電機(jī)節(jié)點(diǎn)為PV節(jié)點(diǎn)。IEEE 30節(jié)點(diǎn)系統(tǒng)優(yōu)化后結(jié)果如表1所示。
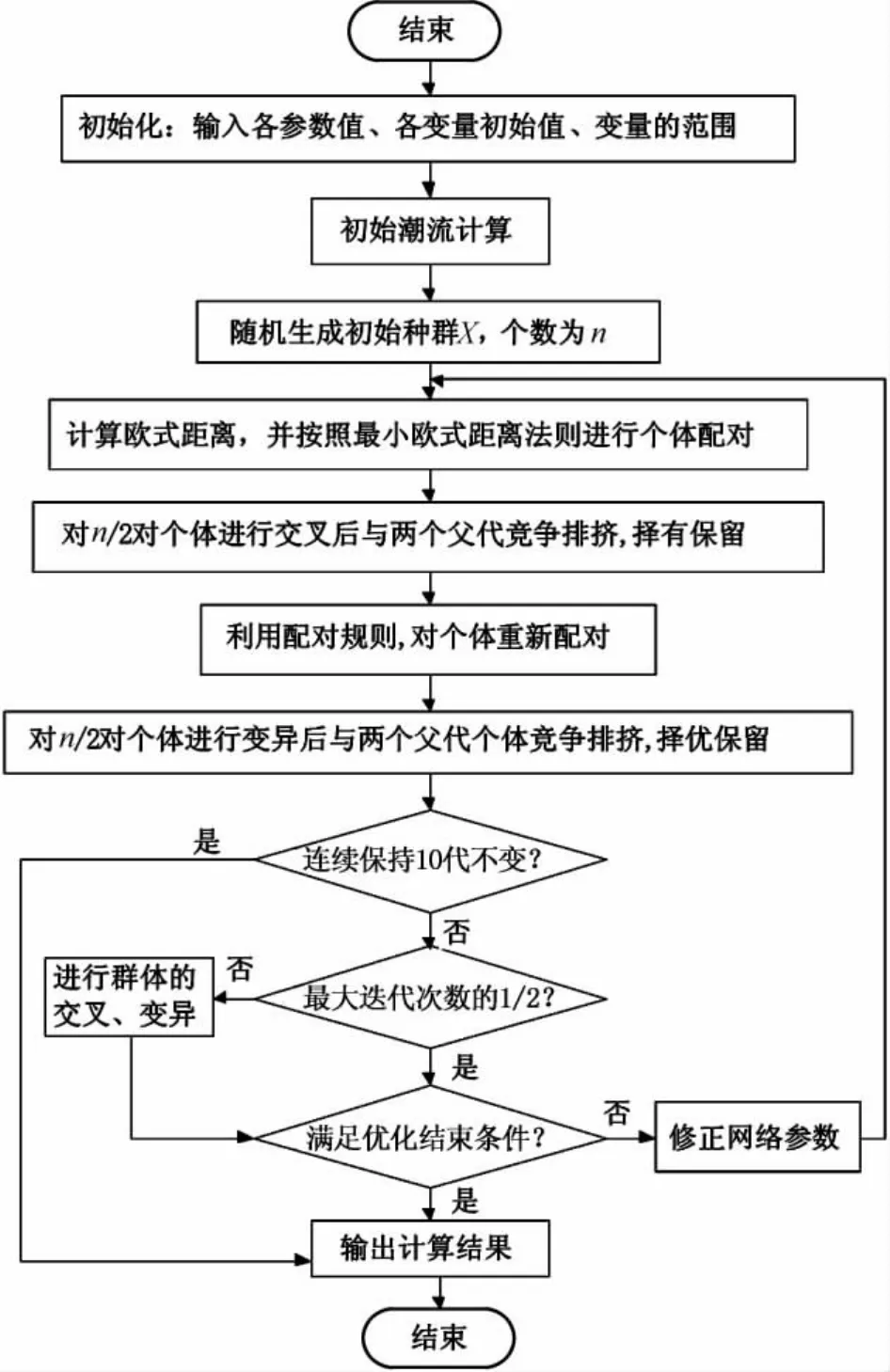
圖1 基于(1+1)GA求解無(wú)功優(yōu)化的流程圖
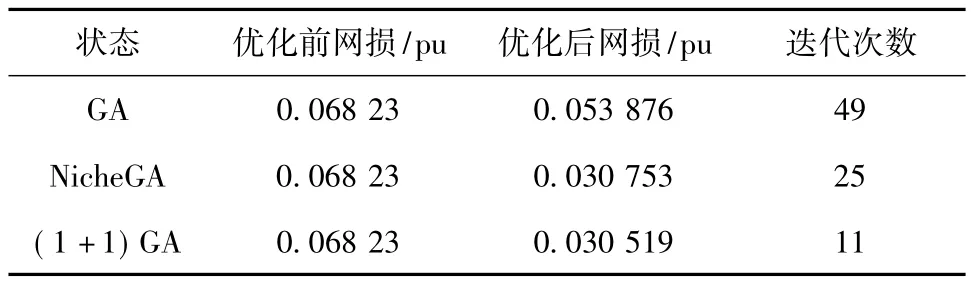
表1 IEEE 30節(jié)點(diǎn)系統(tǒng)優(yōu)化后結(jié)果
從表1中結(jié)果可看出:在優(yōu)化后,系統(tǒng)有功網(wǎng)損由原來(lái)的 0.068 23下降到 0.030 52,減小了0.037 71,迭代次數(shù)由原來(lái)的49下降到11,可見(jiàn),(1+1)GA不僅提高了該系統(tǒng)的安全性和經(jīng)濟(jì)性,而且在計(jì)算的迭代次數(shù)上,小生境遺傳算法明顯低于一般遺傳算法和小生境遺傳算法,以更快的收斂速度獲得更優(yōu)的解,提高了計(jì)算速度。
5 結(jié)束語(yǔ)
在解決無(wú)功優(yōu)化問(wèn)題上,應(yīng)用了最小歐氏距離下(1+1)競(jìng)爭(zhēng)小生境遺傳算法,通過(guò)采用自適應(yīng)交叉、變異算子和考慮是否連續(xù)10代解保持不變,提高了計(jì)算速度和收斂速度,利用迭代前期整體解空間的動(dòng)態(tài)交叉和變異,提高了全局搜索能力。對(duì)IEEE30節(jié)點(diǎn)系統(tǒng)進(jìn)行了優(yōu)化計(jì)算和分析,結(jié)果表明該算法對(duì)電力系統(tǒng)無(wú)功優(yōu)化具有穩(wěn)定、高效、更好的全局尋優(yōu)能力和收斂速度。
[1]李惠玲,盛萬(wàn)興,張學(xué)仁,等.改進(jìn)小生境遺傳算法在電力系統(tǒng)無(wú)功優(yōu)化中的應(yīng)用[J].電網(wǎng)技術(shù),2008,32(17):29 -34.
[2]LAI L - l,MA J- t.Application of evolutionary programming to reactive power planning-comparison with nonlinear programming approach[J].Ieee Transactions on Power Systems,1997,12(1):198-204.
[3]LIU M-b,CANIZARES C A,HUANG W.Reactive power and voltage control in distribution systems with limited switching operations[J].Ieee Transactions on Power Systems,2009,24(2):889-899.
[4]陳奇,郭瑞鵬.基于改進(jìn)遺傳算法與原對(duì)偶內(nèi)點(diǎn)法的無(wú)功優(yōu)化混合算法[J].電網(wǎng)技術(shù),2008,32(24):50 -54.
[5]王振樹(shù),李林川,李波.基于粒子群與模擬退火相結(jié)合的無(wú)功優(yōu)化算法[J].山東大學(xué)學(xué)報(bào)(工學(xué)版),2008,38(6):15 -20.
[6]SERGIO G.Optimal reactive dispatch through interior point methods[J].Ieee Transactions on Power Systems,1994,9(1):136 -146.
[7]WU Q-h(huán),CAO Y -j,WEN J-y.Optimal reactive power dispatch using an adaptive genetic algorithm[J].International Journal of Electrical Power and Energy System,1998,20(8):563-569.
[8]王春香,李現(xiàn)友.最小歐氏距離下(1+1)競(jìng)爭(zhēng)小生境遺傳算法[J].計(jì)算機(jī)與數(shù)字工程,2008,36(11):1 -4.

