賠付率超額再保險風險模型中的鞅方法

沈亞男

(哈爾濱商業大學，黑龍江哈爾濱150028)

一、課題研究背景

隨著高科技的不斷發展和廣泛應用，以及高新產業的大量涌現，大額保險標的日益增多，這些標的一旦發生事故，損失可高達幾千萬，甚至上億美元，遠非一家保險公司所能承擔。為了增強投保人及保險公司的利益保障，再保險應運而生。所謂再保險，也稱為分保，在原保險的基礎上，通過簽訂分保合同，保險公司將其承保的部分或全部風險責任向其他一個或多個保險人進行保險的方式。本文通過對再保險風險模型進行進一步研究，提出了一類帶有干擾項的賠付率超額再保險Poisson風險模型，從而可為保險公司的穩健經營提供可靠的理論保障。

二、賠付率風險模型的建立

(一)相關準備

賠付率超額再保險是指按年度賠款與保費的比率來確定自負責任和再保險責任的一種再保險方式。在約定的年度內，當賠付率超過分出的自負責任比率時，超過的部分由再保險公司負責。賠付率超額再保險是以原保險人一段時間(一般是1年)的總損失額為理賠基礎。記Ci為單位時間收取的保費，單位時間是以年為單位，Xi(i=1，2，……)為第i年的理賠額。則原保險公司的賠付模型表示為：

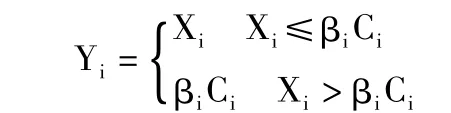
式中：βi是第i年約定的自負責任比率，(0＜βi＜1)。

(二)模型的建立

(Ω，F，P)表示一個完備的概率空間，以下隨機過程(變量)均定義在該空間之上。

①u≥0是保險公司初始資本;

②{N(t)，t＞0}是一個齊次Poisson過程，其強度分別為σ，且N(0)=0，它表示［0，t)時間內(規定到整年止)接受保險業務的年數;

③{Ci，i=1，2，……}，{Xi，i=1，2，……}分別是取值于(0，+∞)的獨立同分布隨機變量序列，設E［Xi] =λ1，E［Ei] = λ2，實際意義如前所述;

④{W(t)，t＞0}是一標準的布朗運動，時刻t的均值為0，方差為t的正態分布，它表示保險公司的不確定性付款或投資收益，作為干擾項，ρ為干擾因子;

⑤CR表示再保險費率

假定{N(t)，t＞0}、{Ci，i=1，2，……}、{Xi，i=1，2，……}、{W(t)，t＞0}是相互獨立的。則

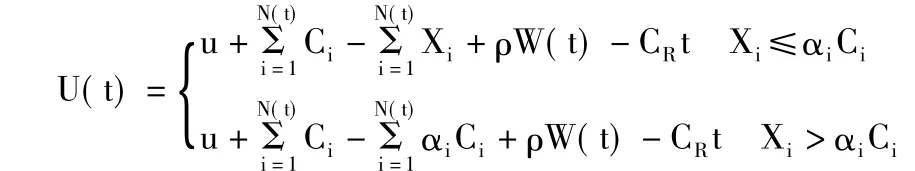
稱{U(t)，t≥0}為帶干擾的賠付率超額再保險的Poisson風險模型，它表示保險公司到時刻t后的總資本;

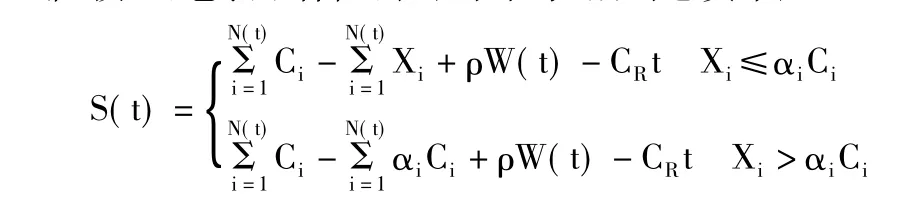
稱為到時刻t后的盈余資本。為了保證保險公司經營的持續性，E［S(t)] ＞0，即

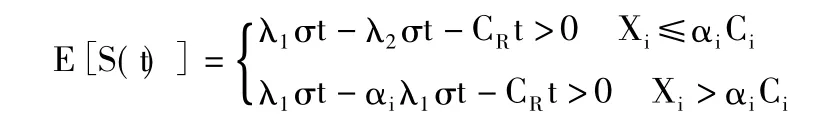
于是，記 Tu=inf{t：U(t) ＜0，t＞0}，inf? = ∞，T 為保險公司有賠付率再保險情況下首次破產的時刻，即首次盈余為負的時刻，簡稱為破產時刻;記ψ(u)=Pr{TU＜∞|U(0)=u}為再保險條件下，初始盈余為u情況下破產發生時的概率，稱其為最終破產概率，簡稱破產概率。并且假定 Ci，Xi(i=1，2，…)的矩母函數均存在，即存在r＞0，使得 MXi(r)=E［erXi] ＜ + ∞ ，MCi(r)=E［erCi] ＜+∞。

三、相關引理

引理1 盈利過程{S(t)，t≥0}是一個右連續隨機過程，且具有下列性質

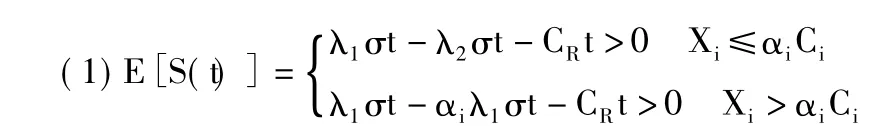
(2)具有平穩獨立增量性;

(3)存在正數r，使得E(e-rS(t))＜+∞;

(4)存在函數g(r)使得E［e-rS(t)] =etg(r);其中g(r)

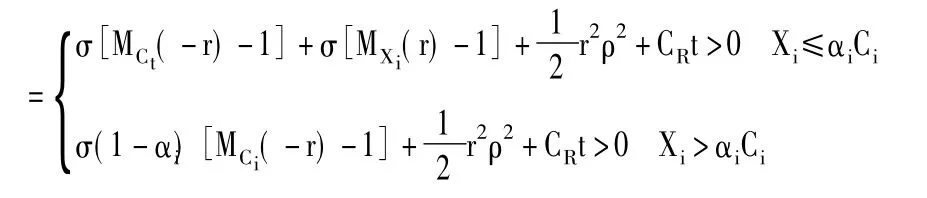
MXi(r)=E［erXi] ＜ + ∞，MCi(r)=E［erCi] ＜ + ∞分別為年理賠額和保費的矩母函數。證明：(1)，(2)，(3)顯然成立。

(4)證明如下：

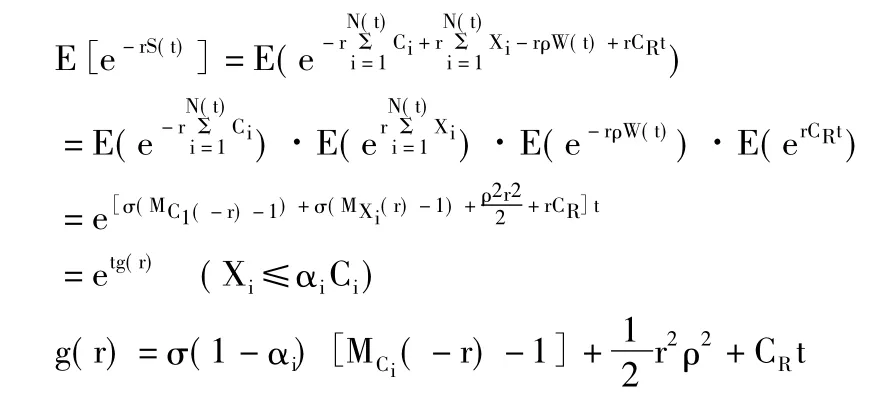
Xi＞αiβi同樣可證引理2對于任意的r，令Au(t)=則{Au(t)，t≥0}是鞅。其中定義事件流FSt=σ{FNt∨FWt，t≥0}。

證明：由Au(t)可測，且E|Au(t)|＜+∞，對于任意的0＜m≤t。

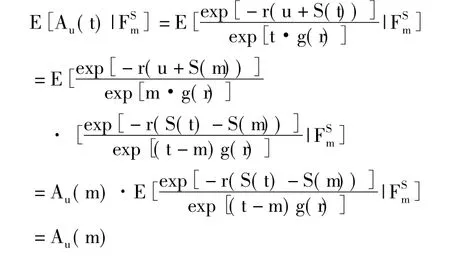
{Au(t)，t≥0}是鞅。

引理3 存在惟一的正常數R，使得g(r)=0，稱R為調節系數。其中g(r)如引理1所示。

引理4 Tu是停時。

四、結論

定理：在賠付率超額再保險風險模型{U(t)，t≥0}下，最終破產概率仍滿足Lundberg不等式ψ(u)≤e-Ru;最終破產概率仍滿足公式其中，稱為調節系數。

證明 因為Tu是停時，選取t0＜+∞，易知t0∧Tu是有界停時，根據引理1和有界停時定理有

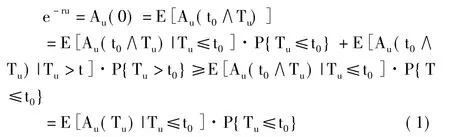
由于在{Tu＜∞}的條件下，u+S(Tu)＜0，

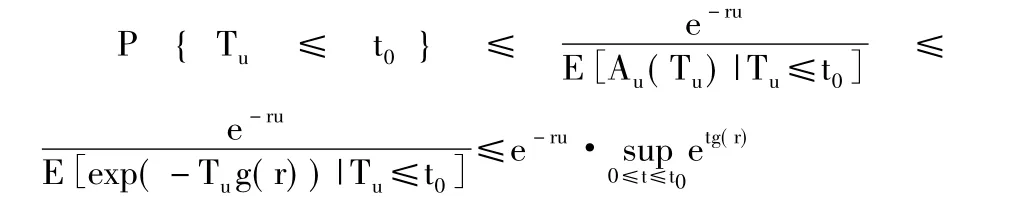
上式兩端令t0→+∞，得

ψ(u，φ，h)≤e-ru·et·g(r)

取R=sru＞p0{r：g(r)≤0}

所以 ψ (u，φ，h)≤e-Ru

根據上(1)式，取r=R得

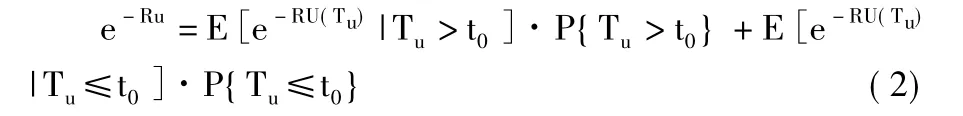
I(A)表示集合A的示性函數，有

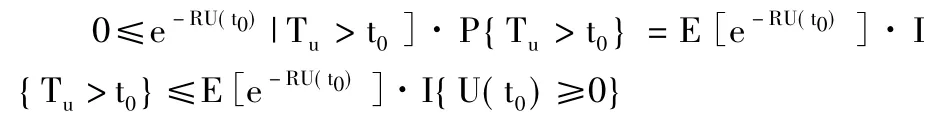
由于0≤e-RU(t0)·I{u(T0)≥0}≤1且根據強大數定律可證當時t0→+∞

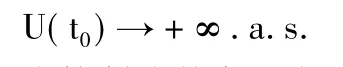
由控制收斂定理有

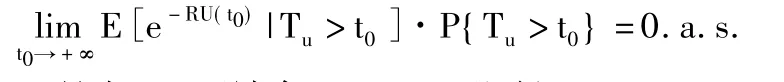
于是在(2)兩端令t0→+∞，即得

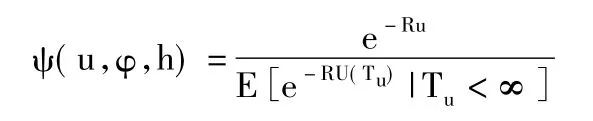
證畢。

基于保險公司的實際運營還有很多不確定因素，如利率、不確定付款和收益等，還有待于對完善的再保險風險模型進行進一步的分析研究。另外，保險公司經營的險種往往不是一種或幾種，多險種的再保險風險模型仍需繼續深入探索，為保險公司的實際運營提供可靠的理論依據。

［1] 唐國強，楊端翠．成數再保險和超額賠款再保險策略［J] ．廣西科學學院學報，2006，22(1)：58-60．

［2] 粟芳，許謹良．保險學［M] ．北京：清華大學出版社，2006．

［3] 孔繁亮．B值漸進鞅的強弱大數定律［J] ．數學學報，1998，41(3)：667-672．