解決薄殼體靜態磁場反演問題的新方法

徐 杰

(海軍駐桂林地區軍事代表室，廣西桂林541002)

0 引言

現在越來越多的應用軟件能夠解決反演問題。本文關注靜態磁場的反演問題。將1個沒有磁化的鐵磁性物體，放置于1個外圍磁場中，通過磁傳感器測量磁場值，然后計算出任何位置的磁場，尤其是不能放置傳感器的地方。本文將采用應用于3D薄殼結構的新方法，該方法避免了采用以前的調整方法，減少傳感器的數量。

1 反演公式

1.1 經典公式

將1個鐵磁性外殼物體放置于外部磁場H0中(地球磁場或者線圈產生的磁場)。殼體的磁矩M包括2個部分:感應部分Mind，由外部磁場引起;固定部分Mper，材料的歷史磁性。由于周圍磁場變化而引起的磁化，用Hred表示。

如果薄片的厚度小而且相對滲透率μr高，則假定磁化切線于中間曲面S［1］。將薄殼體剖分成N個相同的磁化單元。磁矩M與標準磁矩Hred的關系為

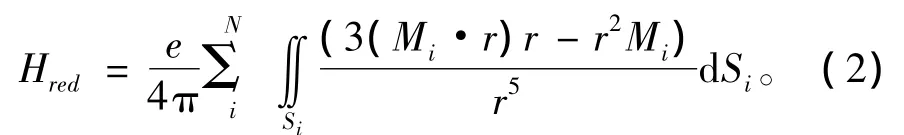
其中，r為薄殼體和曲面S的聯結點與傳感器之間的矢量。

1.2 奇異值的減少

式(2)表明，在1/r3數量級下，殼體附近存在奇異值的問題。為減少奇異值，每個單元殼體采用經典結論。分析具有相同磁化的容積V，得

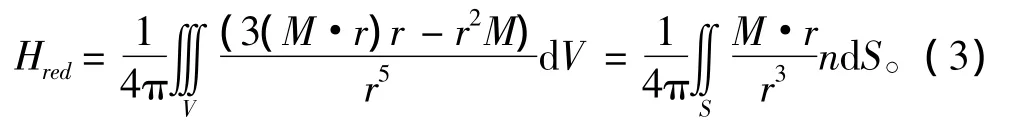
其中n為V的外部法線。將式(3)應用到單元Si，得到新公式

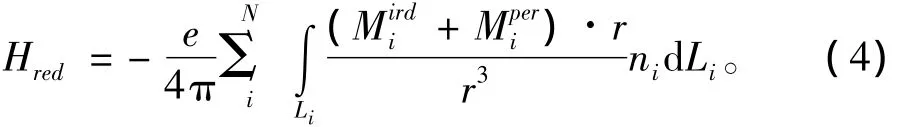
其中ni為單元Si厚度方向的外部法線。式(4)表明，在1/r2數量級下的奇異值，是計算值最接近于殼體的實際值。

1.3 系統論述

放置P個傳感器于空氣中，得到1個具有4×N個未知數的3×P個方程 (傳感器為3個軸向)，從而得到以下系統

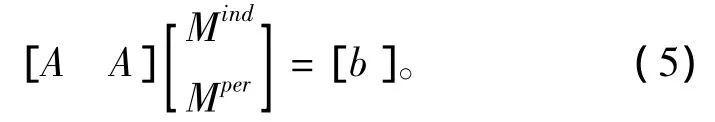
其中:A依賴于網格和傳感器的位置;b為測量磁場部分。一般情況下，測量數據多于方程的未知數。此系統非常龐大 (尤其對于3D幾何學)，并且一些方程是矛盾方程 (因為測量數據不精確)，因該系統具有病態性，必須采用優化方法。

2 殼體內部的有效方程式

經典優化方法基于已知信息 (大部分情況為標準方案或者由此派生的方案最小值)。因此，為解算式(5)，通過增加1個系數，使之變為1個新的良性數學系統。盡量將物理方法代替數學方法來解決此問題，則有

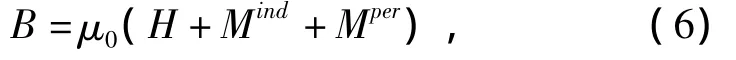
殼體內部的有效公式

綜合式(6)和式(7)，得到另1個公式

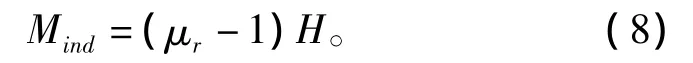
其中:H為殼體內部某位置的磁場值，由H0和所有薄片的磁化引起。聯合式(4)，得到單元i的1個新公式

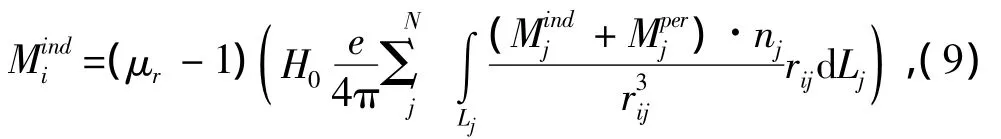
將式(9)應用到每個薄片單元上，得到

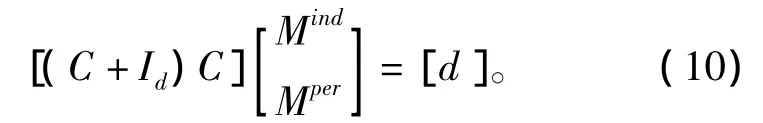
式(10)由2×N個方程和4×N個未知數組成，方程個數比未知數少，但是具有很好的條件數。目前，采用最小正方形方法解算式(6)和式(10)。由此可見，僅僅解算式(10)將引起感應磁化的微積分，并且使固定磁化變為0。

3 計算與試驗結果

重點關注鐵磁船體產生的異常磁場。建造1個真實的船模 (長4.6 m，e=1.4 mm，μr=96)，用來驗證運算法則。外部磁場H0是地球磁場，32個三軸傳感器放置于艦船內部，艦船被剖分為271個小單元 (見圖1)。通過測量殼體內部的磁場以及采用前文方法，得到磁化模型 (見圖2)，計算出艦船外部磁場，并且將此磁場值與殼體下方30 cm處的縱向方向的測量值進行比較。

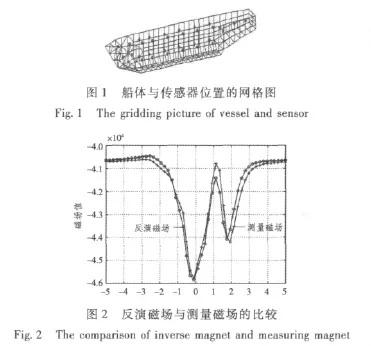
4 結語

本文介紹一種解決靜態磁場反演問題的新方法，并且在船模上驗證了該方法。與過去方法相比，該方法具有明顯優點。首先，它降低了式(2)奇異值的次冪，使傳感器更接近于磁源 (例如殼體)，并且得到更多精確的測量數據。其次，通過給殼體內部增加一個物理系統，更有利于分析問題。少量的測量裝置(例如傳感器)可以得到可靠的解決方法，并且系統具有良好的條件數。該方法既有規律性又有可供選擇的良好參數 (對于3D殼體來說，選擇參數非常困難)，此外，它能夠方便地應用于大容積裝置。

［1］CHADEBEC O，COULOMB J L，LECONTE V，BONGIRAUD J P，CAUFFET G.Modelling of static magnetic anomaly created by iron plates［J］.IEEE Trans.Magn，2000，36(10):667-671.

［2］IGARASHI H，KOST A，HONMA T.Inverse inference of magnetizationdistribution in cylindrical permanent magnets［J］.Proc.Compumag’99，1999，2:310-311.