動平衡儀設計方法

張贊秋 孫 振 高 巖 羅 迪 李 俊

（大連光洋科技工程有限公司，遼寧大連 116600）

軸類旋轉類件在高速旋轉時，由于密度不均勻或者由于特異的外形將導致對支撐部位周期性的擠壓或者拉伸，長時間將導致軸承的加速磨損和支撐物的金屬疲勞，最終導致不可預計的安全隱患。因此對此類物件在使用前做基本運動平衡補償是必須的，傳統方式需要將被平衡物件拆卸后利用專用平衡機測量和補償。本文描述的方法采用柔性比例估算方法，利用物件原始支撐不需要拆卸即可完成所有的補償工作，可以提高工作效率和補償成本。

1 平衡計算原理

當物體旋轉時，如在徑向存在不平衡，所有的不平衡量都可以遞歸到一個不平衡的質點和一個對應的有效半徑，因此只要找到這個質點和有效半徑，并且對此

質點做對應的反補償，就可以平衡掉原有的不平衡量。

2 動平衡實現的方式

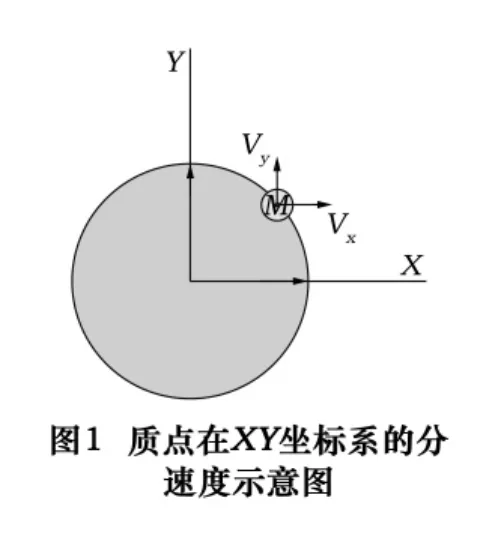
如圖1所示，當物體以角速度ω旋轉時，任意質點在XY坐標系的分速度分別為

其中θ為質點M的向徑與X軸的夾角。

對式（1）、（2）求一階導數得:

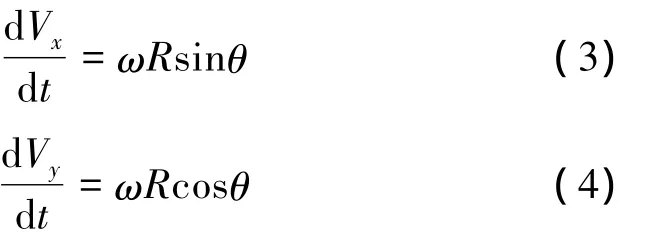
因此對于質點M，在XY方向的應力為

由式（5）、（6）可以看出當物體勻速旋轉時，在X和Y方向的向心應力為一個正弦值。任何剛性支撐物都可以認為是一個彈性模型，即滿足

式中:F為作用力;X代表形變有效形變量;k代表不同彈性模型的勁度系數。

因此滿足在XY方向上有

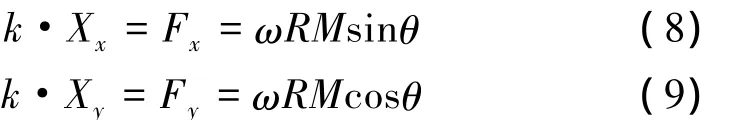
由式（8）、（9）可以看出，在XY方向的位移同樣是一種滿足正弦加速的位移，也就是說通過測量支撐物的加速度就可以間接地測量出旋轉部分的不平衡量。

3 實際存在的問題

采用轉速傳感器和加速度傳感器對被測物的支撐體測量，尋找的被測物最大形變量的值，通過轉速傳感器對角度定位，就可以得到補償點位置和補償質量。

3.1 復合的信號與噪聲問題

對于一個機械體，其在運行時往往是復合的特征反映，即在機械上所有的振動都將是一個相互耦合的關系，如圖2所示。

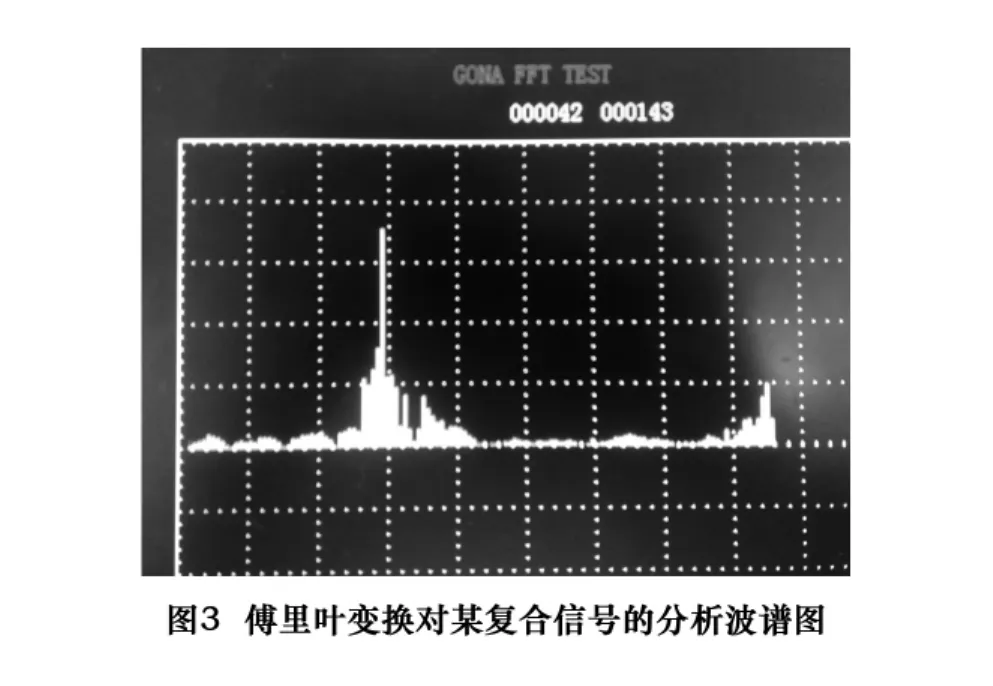
圖2表示的是某個帶有小直徑小慣量旋轉部件的復合支撐物的振動波形圖，由圖可以看出所有的特征量被淹沒在一片噪聲中，因此對于有效直徑小、不平衡量很小的旋轉物體和剛度支撐較強的物體，希望直接利用加速度傳感器和轉速傳感器，利用傳統直接測試的方法基本是不可能的，因此必須采用某種方法對其有效信號進行提取。采用傅里葉變換可以精確對特征頻率提純，而且可以得到某個特征頻率的幅值。

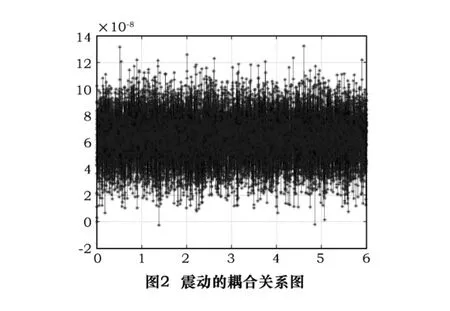
圖3是利用傅立葉變換對某復合信號的分析波譜圖，由圖可以明顯看到特征頻率和幅值大小。因此利用傅里葉變換對振動進行頻譜分析從而得到特征頻率是有效而精確的。

對于傅里葉變換來說，當實際頻率超出采樣頻率的上下限時，在頻譜圖上將產生虛假頻率，在計算時帶來不必要的干擾誤測。因此在采樣之前必須對信號經過帶通濾波處理，使被采樣信號處在采樣頻率的極限之內，然后再進行頻譜變換分析。

對于被測物體來說，情況是千差萬別的，例如旋轉部件的直徑和最高轉速。有些最高轉速很低，例如大型轉臺60 r/min（1 Hz），電主軸30 000 r/min分（500 Hz），因此前級的帶通濾波器的帶通比為500∶1，這種寬范圍的帶通濾波器在現實中是不存在的，因此必須采用多通道帶通濾波器選擇濾波，并且為求更好的下行斜率每級采用2級帶通濾波。

3.2 信號的幅值與精度問題

由于旋轉部件的支撐物的剛度（勁度系數）差異和不平衡量各不一樣，因此當振動量很小或支撐物剛度較強時，加速度傳感器的輸出幅值很小，造成采樣精度過低。因此動平衡測試設備在前級輸入端進行增益選擇切換是必須的，以應付不同的輸入幅值，提高補償精度。

支撐物體的剛度不一致，必須求得支撐物體的剛度（勁度系數）才能最終得到需要的補償量，也就是說必須對補償量進行定標處理。因此在測量時首先對被測體進行測量，然后在被測體的隨意位置安裝一個已知質量、有效半徑和角度的物體。然后再次測量，得到兩次測量的差值，就可以推算出真實需要的補償量的大小和位置。

4 實際問題分析與解決方案

4.1 噪聲問題的處理

AD轉換采樣采用FPGA定時方式，為了提高數據的自我噪聲抑制能力，采樣采用硬件定時，采樣后的數據由數學方式做濾波后進行FFT運算。

4.2 信號幅度的處理

由于信號幅度的不同，因此，信號在進入AD轉換器進行轉換前，采用了可變增益放大器進行數據放大倍數變更，此過程是一個自動完成的過程。

5 采用的方案

采用FFT處理器，為了提高運行速度，FFT運算采用硬件運算方式。

5.1 FFT 原理

快速傅里葉變換（FFT）是計算N點離散傅里葉變換（DFT）的高效算法，通常輸入的序列為復數，利用對稱性組合可以對實數實現更高效的DFT變換。

DFT是連續傅里葉變換的離散形式，模擬信號x（t）的連續時間傅立葉變換表示為

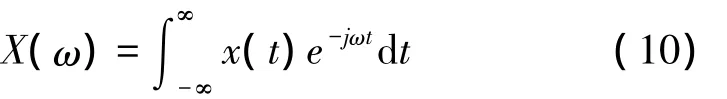
x（t）經抽樣后變為x（nT），T為抽樣周期。離散信號的傅里葉變換表示為

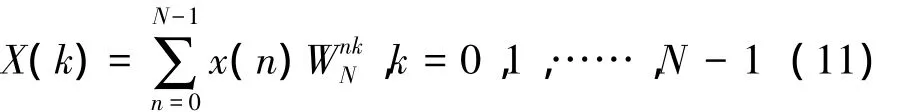
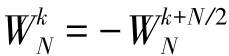
這樣，利用這些特性可以使DFT運算中的某些項合并，可以將長序列的DFT分解為短序列的DFT。

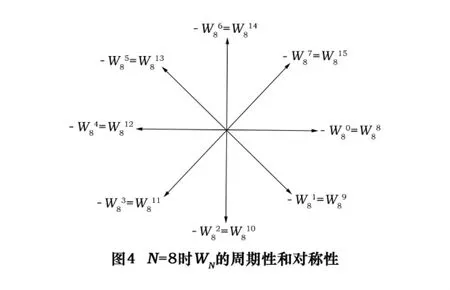
FFT算法分為時間抽取FFT（DIT）和頻率抽取FFT（DIF），DIT是將N點的輸入序列x（n）按照偶數和奇數分解為偶序列和奇序列，因此，x（n）的N點FFT可表示為

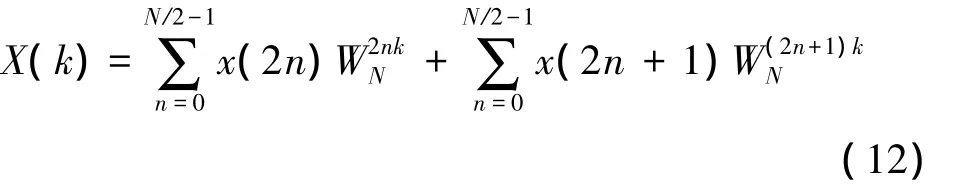
根據

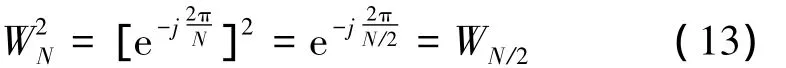
得:

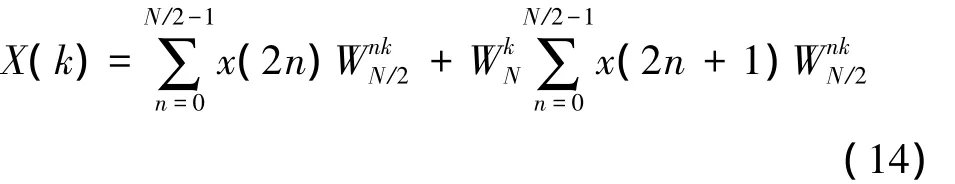
用X1（k）和X2（k）分別表示式（14）右邊第一項和第二項求和運算式，則有:

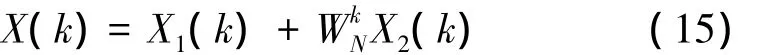
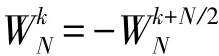
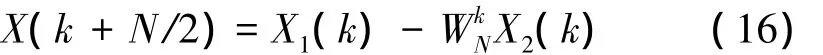
同理，進一步可得N/4點的FFT，重復抽取即可得2點FFT。在基－2FFT中N=2M，共有M級運算，每級有N/2個2點FFT蝶形運算，因此N點FFT共有（N/2）log2N個蝶形運算。基－2 DIT的FFT蝶形運算如圖5所示。

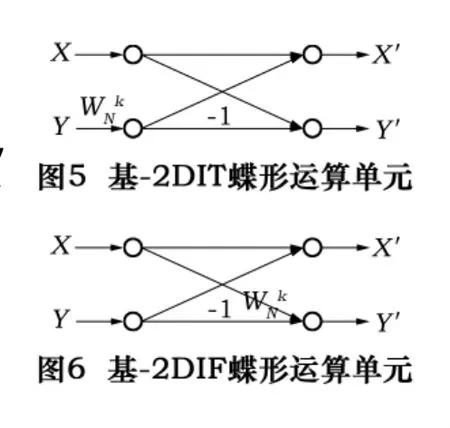
DIF算法與DIT算法在本質上是一樣的，在運算量與復雜性方面也完全相同，只不過它是把輸出序列X（k）按其順序的奇偶分解為越來越短的序列，這里只給出DIF的基本運算單元，如圖6所示。

5.2 FFT處理器原理框圖

FFT處理器的主要功能是對采集得到的數據進行512點FFT運算。其原理框圖如圖7所示。

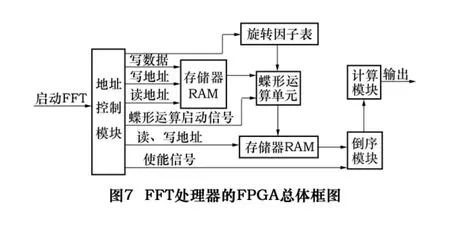
地址控制模塊負責產生讀地址、寫地址、使能信號以及相關模塊的啟動、控制信號，是本模塊的核心;雙口RAM負責對外部輸入的原始數據進行緩存;蝶形運算單元完成2點DFT運算;旋轉因子表實質上是一個ROM，用來存儲每一級FFT運算所需要的旋轉因子;暫存器RAM用來暫存經過蝶形運算后的中間數據;倒序模塊實現頻譜正常順序輸出;由于FFT的運算結果是復數，所以還需要對數據進行模值、相位角運算。

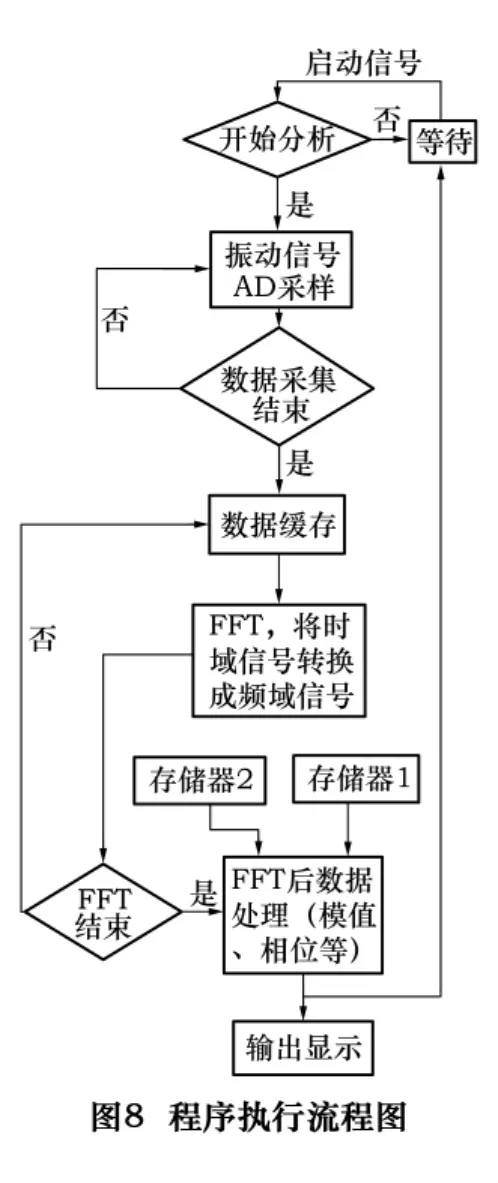
5.3 程序執行的過程

程序的執行如圖8所示。

5.4 GUI的移植過程

在NIOS IDE的C/C++Build選項中的General中添加路徑，需要添加的有 Config、Core、Widget和 WM的路徑。根據需要修改編寫里面的配置文件以及底層驅動即可。

5.5 產品的技術指標

（1）測試轉速范圍30～61 000 r/min（轉速變化小于±2%），誤差小于±1 r/min;

（2）相位測量0 ～360°，分辨率:1°;

（3）振動速度范圍0.1～1 000 mm/s，分辨率為±0.1 mm/s;

（4）振動位移范圍0.001 ～999 μm（轉速為1 200 r/min 時），分辨率為±0.001 μm;

（5）振動測量和頻譜分析頻率響應為0.5 Hz～1 kHz;

（6）動平衡校正方法為單、雙面平衡，極坐標和分力校正方式;

（7）動平衡校正配重為添加或削減方式，參考試重為保留或去除方式;

（8）振動分析觸發通道數量為2個;

（9）振動分析觸發為8級;

（10）采用7英寸彩色LCD觸摸顯示屏用于圖像數據顯示和輸入;

（11）支持多國語言。

6 方案的產品驗證

采用以上的分析方式，成功完成了GDS1000在線式動平衡儀的開發工作，經過使用比較，完全達到設計目標，與日本理音公司和西格瑪公司的同類產品性能和測試精度相同。產品如圖9所示。