隧道開挖釋放荷載的有限元模擬方法研究
陶 星
(中鐵二院工程集團有限責任公司地下鐵道設計研究院,四川成都610031)
隧道工程區別于其它建筑工程的特點之一是其不斷地開挖和支護,對開挖的模擬是隧道數值分析中的重要問題之一。從理論上講,隧道的開挖模擬是三維空間黏彈塑性問題,但是由于三維分析工作量巨大,要花費大量的時間進行前后處理和數值計算,因此,往往將其簡化為平面應變問題,采用二維分析方法,此時,工作量將成倍減少,容易被工程技術人員掌握,且在正確的模型和邊界條件下也可得到滿意的結果。
在二維分析中,為了模擬掌子面的空間支護效應,多采用應力釋放法進行分析,而釋放荷載的選取對計算結果有重要影響。盡管采用有限元方法進行隧道數值分析已有很長的時間,也積累了很多的經驗,但是對軟件的理解和操作不當,經常會得出錯誤的結論。本文針對隧道開挖釋放荷載的模擬方法進行了對比總結,為正確使用軟件進行隧道開挖模擬提供科學依據。
1 幾種開挖釋放荷載的計算方法
1.1 Mana[1]法
所謂開挖釋放荷載實際上是被開挖掉的那部分單元通過開挖界面與剩下的單元之間的相互作用力,因此在開挖前它在本質上是內力。每一次開挖使得所暴露出來的表面為自由表面,即無應力狀態,此時,需要將相互作用力反方向施加在開挖剩余體系上。
記被開挖掉的那部分單元的全體為ΩE,SE是開挖邊界,作用在ΩE上的外載除了SE上的面力荷載p(開挖荷載)外,還有體積力b(自重或滲流力),由它們產生的內力σ,因此有

上式第一項即為開挖引起的等效節點力fE,因此

但目前大多數有限元程序給出的開挖荷載僅含上式右邊的第一項,也就是Mana提出的應力直接積分法。實際上這是不對的[2],例如b是密度時,傳統的計算方法就未計入重力對開挖荷載的貢獻。由于開挖往往引起卸荷破壞,因此傳統的計算方法可能會低估破壞區,且開挖體的埋深越淺,所引起的偏差就越大。
在隧道開挖模擬過程中,先進行初始應力計算,然后根據Mana公式計算釋放荷載,在除去開挖體的結構上向洞內施加(反轉應力)等效節點力,計算應力增量和位移增量,然后疊加初始應力場得到二次應力場,位移增量為開挖引起的擾動位移,具體過程見圖1。
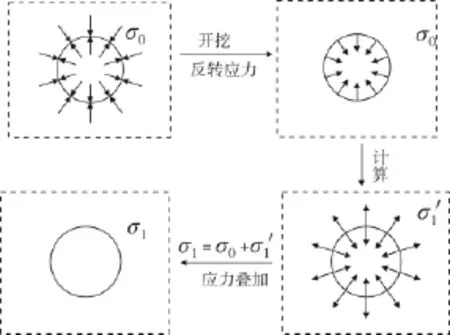
圖1 開挖釋放荷載計算過程
1.2 剛度折減法
此法由Swoboda教授[3]提出,也稱剛度逐步軟化法,即對開挖單元的彈性模量乘以一個軟化系數α,模擬應力逐步釋放,在襯砌施工完成后,開挖單元的彈性模量為零,具體過程見圖2。
此法雖沒有嚴格的理論基礎,軟化系數的選取帶有很大的任意性,但是易于在通用有限元程序中實現,如果能結合現場測試結果,確定每次施工合理的軟化系數,不失為一種很好的模擬方法。
1.3 支撐荷載法
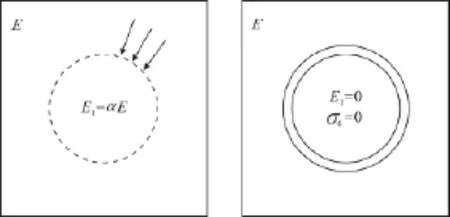
圖2 剛度折減法原理
隧道的開挖打破了開挖邊界上各點的初始平衡狀態,開挖邊界上的節點力不平衡,會產生新的變形,引起應力重分布。此時可以“殺死”開挖單元,即開挖單元具有“零應變”狀態,為了克服方程的病態性,將開挖單元的剛度乘以一個很小的系數,同時約束位移。此時,可在上一步的基礎上繼續進行求解,應力狀態自動進行疊加,位移需減去初始狀態。上述方法稱為“地應力自動釋放法”,也是目前通用有限元程序采用“生死單元”模擬開挖的方法。如果在開挖邊界上施加虛擬的支撐力,來模擬圍巖的逐步卸載,就是支撐荷載法[4]。文獻[5]詳細討論了支撐荷載的作用方向、選取方式及釋放系數的取值,不再贅述。
支撐荷載和釋放荷載作用方向相反,且有如下關系,設每一步開挖的荷載釋放系數為αi,第n步開挖的釋放荷載為αnfi,則支撐荷載為:
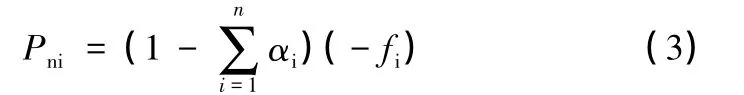
對于分布開挖,可按上式分布施加支撐節點力,具體見圖3。
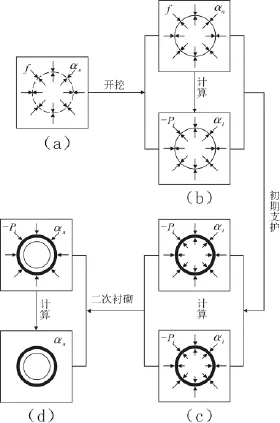
圖3 支撐荷載法計算過程
2 從體系平衡觀點看釋放荷載計算
在數值計算中,可以從兩種角度分析開挖對體系的作用。
(1)開挖解除了卸載部分對剩余部分的作用力,使剩余部分失去平衡,所以可對卸載部分對剩余部分的作用力進行分析,也就是對卸載部分進行分析,具體實現方式就是開挖釋放荷載的計算(Mana法等),這種思路稱為開挖的間接分析。
(2)任一時刻,體系保持平衡或者失去平衡都是體系內力和外力共同作用的結果,開挖將卸載部分的內力轉化為剩余部分的外力,故可以對剩余部分進行分析,完全放棄釋放荷載的概念,更容易保證分析的可靠性,這種思路稱為開挖的直接分析,支撐荷載法和軟化剛度法都屬于這種思路。
可以從體系平衡的有限元數值格式上證明,這兩種方法是等價的,但實現的難易程度是不同的。
3 結論
本文總結了隧道開挖釋放荷載的有限元模擬方法,從開挖分析的間接和直接分析思路得出幾點結論:
(1)Mana法是一種間接計算開挖作用的分析方法,計算繁瑣,經常需要自己編程計算等效節點力,且忽視體積力的影響,不適宜采用通用有限元軟件分析。
(2)剛度折減法沒有嚴格的理論依據,軟化系數的選取帶有很大的任意性,但最容易在通用有限元程序中實現。
(3)支撐荷載法是一種直接考慮開挖作用的分析方法,理論嚴密、概念清晰,比較容易在通用有限元程序中實現,且計算過程應力場和位移場自動疊加,非常適合多施工步開挖的模擬。
[1]Mana A I,Clough G W.Predicition of movement for braced cuts in clay[J].Geotechnical Engrg Division,1981,107:759-778
[2]鄭宏,葛修潤,谷先榮,等.關于巖土工程有限元分析中的若干問題[J].巖土力學,1995,16(3):7-11
[3]SWOBODA G,EBNER H,WANG S J,ZHANG J M.Application of the decoupled finite element analysis in tunneling[A].Numerical Methods in Geomechanics[C].Rotterdam:Balkema,1988:1465-1472
[4]孫均.地下工程設計理論與實踐[M].上海:上海科學技術出版社,1996
[5]高峰,孫常新.隧道開挖模擬的支撐荷載法研究[J].中國公路學報,2010,23(4)

