駕駛室彈性對某輕卡平順性影響的仿真分析

木 標，尚曉敏，張代勝

Mu Biao, Shang Xiaomin, Zhang Daisheng

（合肥工業大學 機械與汽車工程學院，安徽 合肥 230009）

0 引 言

汽車行駛平順性是指汽車能吸收行駛時所產生的各種沖擊和振動的能力，保持汽車在行駛過程中產生的振動和沖擊對乘員舒適性的影響在一定界限之內，這是評價汽車使用性能的一項重要指標。該性能的優劣直接影響到汽車其他性能的發揮和車輛的使用壽命，同時車輛行駛平順性好壞也直接關系到汽車在市場中的競爭力[1]。

在以往的貨車平順性研究過程中，發現車架彈性對于整車平順性有很大的影響[2-4]，而把駕駛室看成剛體，在進行運動分析中忽略它的彈性變形。而實際上，汽車行駛過程中，路面不平度對駕駛室的沖擊會使駕駛室產生一定的變形。如果考慮車身的彈性變形，可以更真實地評價整車的平順性。所以要研究剛體駕駛室和彈性駕駛室對于整車行駛平順性仿真分析的影響。另外，考慮到駕駛室懸置是整車的二級懸架，對這兩種駕駛室模型在橡膠駕駛室懸置和半浮式駕駛室懸置這兩種情況下的整車行駛平順性也做了仿真分析比較。

文中以某貨車為研究對象，在有限元分析軟件Hypermesh中建立駕駛室的有限元模型，并在Hypermesh中導出駕駛室的模態中性（MNF）文件，再運用ADAMS軟件分別建立整車的剛柔耦合模型和剛體模型，并利用 ADAMS的平順性分析模塊 Ride，將兩種模型在兩種不同駕駛室懸置情況下進行對比仿真分析。

1 整車基本特征參數

影響汽車平順性分析精度的一個主要因素是汽車模型的參數精度，所以在模型建立過程中盡可能使參數最大程度地接近實際值變得很重要。整車特征參數包括運動學參數、質量參數、力學特性參數。獲取模型參數的方法有：試驗法、計算法、CAD 建模法、圖紙查閱法等[5-6]。根據某公司提供的CATIA模型，以及CAD圖紙和相關數據文件，得到整車基本特征參數：駕駛室質量425 kg，整車整備質量3280 kg，軸距3815 mm。

圖1～圖3給出橡膠懸置和半浮式懸置元件的部分特性曲線。

橡膠懸置在 3個方向上的阻尼系數均為 0.5 N?s/mm。半浮式懸置的阻尼系數為4000 N?s/mm。

2 彈性體駕駛室模型的建立

將有限元模型與多剛體模型相連接時，由于有限元模型的自由度數較大，因此必須將有限元動力學模型縮減為一個具有較少自由度的模型，這個過程稱為動力縮減。在MSC/ADAMS軟件中采用部件模態綜合法，部件間的模態綜合在有限元分析中通過超單元分析實現，并在 MSC /ADAMS中將超單元模型轉換為彈性體元件連接到多體系統動力學模型中。

在ADAMS中建立駕駛室的彈性體模型前，需要根據廠家提供的駕駛室 CAD模型，在Hypermesh中建立駕駛室的有限元模型，然后在Hypermesh中通過設置相關卡片，將駕駛室有限元模型轉換為 ADAMS可用的模態中性文件，即MNF格式文件。最后通過將駕駛室模態中性文件導入ADAMS中，建立駕駛室的彈性體模型。

3 剛體駕駛室模型的建立

剛體車身模型比較簡單，可以直接利用ADAMS/Car 中自帶的剛體車身模型，整個剛體的質量集中在質心位置，具體位置由整車參數確定，而幾何外形對于所做的仿真沒有影響，所以只是用簡單的幾何外形示意駕駛室輪廓。

4 整車模型的建立

汽車是一個非常復雜的系統，要想建立與實際完全相同的樣機模型，既不現實也沒必要，因此，只對分析結果產生主要影響的部件建立相應的樣機模型，這樣才能在不影響分析精度的前提下，實現快捷有效的建模分析。故在建模時只對懸架系統、車架、車軸和輪胎這幾個對平順性造成主要影響的部件建立相關模型。具體建模時根據得到的相關數據，對軟件中的模型參數進行修改，從而獲得仿真需要的準確模型。圖4、圖5為整車裝配模型圖。

5 隨機路面輪廓的建立

隨機路面生成器（Ride-Profile Generation）是ADAMS／Car Ride提供的一個數字模型的路面生成工具；該模型是基于Sayers經驗模型，綜合了許多不同類型的道路測量參數，可以用于表述實際道路的隨機不平度。可以同時給出左右輪轍路面輪廓參數，模型輸入量的長度單位是 m，輸出左右輪轍的隨機高度為mm[7，8]。

在路面生成器中，取隨機路面生成參數：空間功率譜密度Ge=0，速度功率譜密度Gs=12，加速度功率譜密度Ga=0.17。由路面輪廓生成器生成的B級路面輪廓如圖6所示。

6 平順性的評價

ISO2631：1997（E）標準規定，當振動波形峰值系數＜9（峰值系數是加權加速度時間歷程aw(t)的峰值與加權加速度均方值aw的比值）時，用基本的評價方法——加權加速度均方根值來評價振動對人體舒適和健康的影響。根據測量，各種汽車在正常行駛工況下對這一方法均適用[9-10]，具體計算過程可以參考相關文獻。

7 整車平順性仿真分析

以駕駛員座椅下方地板上一點 3個軸向的加權加速度均方根值作為整車行駛平順性的評價指標，參照前面介紹的評價方法對兩種模型的平順性進行比較分析。在利用ADAMS/Car Ride進行行駛平順性仿真分析時，分別使被測貨車的剛柔耦合和剛體模型以常用車速60 km/h在B級路面上勻速行駛，測量駕駛員座椅下方地板上各個軸向的振動加速度時間歷程[11-12]。圖 7～圖 9和圖10～圖12分別為使用橡膠懸置情況下在剛體模型和剛柔耦合模型中駕駛員座椅下方底板處測得的各個軸向的加速度響應時域曲線。

從圖7～圖12中清晰地表明，垂向加速度響應均大于橫向、縱向加速度響應。可見，垂向加速度響應對于平順性影響很大，這一點在剛體模型中表現得更加突出。而且，在剛體模型中，垂向加速度響應值出現 2個明顯的峰值。

為了分析兩種模型加速度響應的區別，而且考慮到垂向加速度響應對平順性的影響，圖13所示比較兩種模型的垂向加速度時域曲線。

圖13 中實線代表剛柔耦合模型的垂向加速度時域響應，虛線代表剛體模型的垂向加速度時域響應。

通過比較分析，剛體模型的加速度值在兩處位置明顯大于剛柔耦合模型，而在其他位置兩者相差不大，而且兩條曲線在其他位置的走勢非常接近。總體上，剛體模型的垂向加速度響應大于剛柔耦合模型。

根據平順性評價的計算公式，對加速度響應時域曲線在ADAMS/PostProcessor中做FFT運算得到加速度功率譜密度（Acceleration PSD）曲線。這里給出兩種模型的垂向加速度功率譜密度曲線，如圖14和圖15。

從圖中可以看出，在剛體模型中，出現了 2個振動峰值，分別對應2個振動頻率，分別為7.75 Hz和15.25 Hz。而在剛柔耦合模型中，出現了1個主要的峰值，其對應頻率為10.89 Hz。

在以上分析的基礎上，根據公式可以計算出兩種模型情況下駕駛員座椅底板處 3個軸向的加權加速度均方根值和總加權加速度均方根值，如表1所示。

表 1最后一列數值由剛體模型結果減去剛柔耦合模型結果得到，“＋”表示剛體模型結果大于剛柔耦合結果；“－”表示剛體模型結果小于剛柔耦合模型結果。

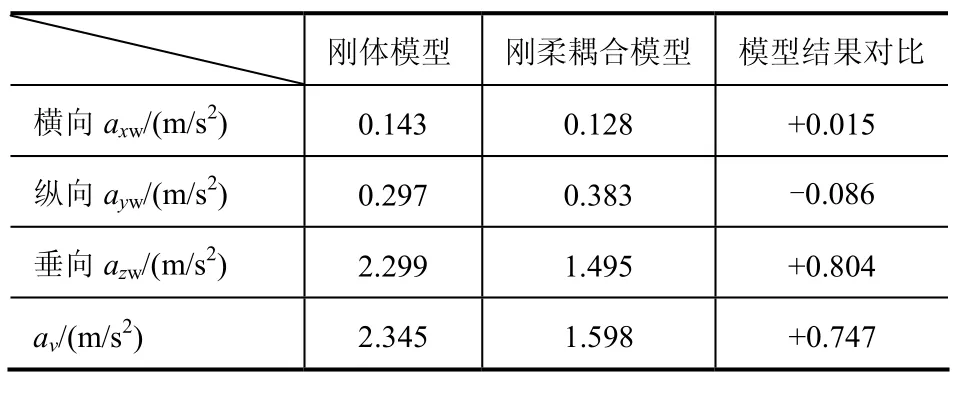
表1 兩種模型不同軸向的加權加速度均方根值和總加權加速度均方根值比較

經過分析表1中數據得出，剛體模型在橫向、垂向以及總的加權加速度均方根值方面均比剛柔耦合模型大，只有縱向加權加速度均方根值小于剛柔耦合模型。從這點不難看出，在懸架系統，車軸以及輪胎不變的情況下，駕駛室剛度越大，整車平順性越差，實際彈性體駕駛室平順性比一般剛體模型預測的要好些。

為了對兩種模型做進一步分析比較，在半浮式懸置情況下，做了相同的仿真，通過計算得出表2。

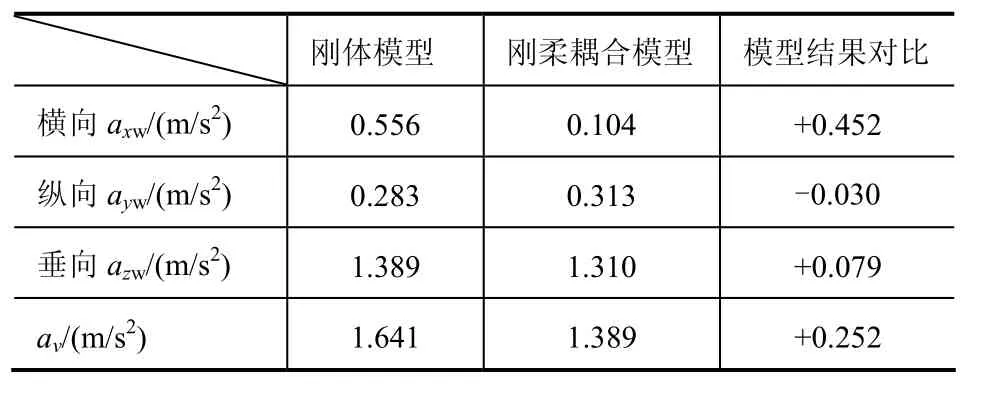
表2 半浮式懸置下兩種模型不同軸向的加權加速度均方根值和總加權加速度均方根值比較

表2最后一列數值含義與表1相同。

通過表 2數據，發現在半浮式懸置下，剛柔耦合模型除了縱向加權加速度均方根值大于剛體模型外，其他方向的值均小于剛體模型；剛體模型的平順性在這種情況下有了明顯的改善，剛柔耦合模型平順性也有了進一步的改善，并且剛柔耦合模型的行駛平順性好于剛體模型，通過比較得出了與前面類似的結果。

要特別說明的是，以上數據是駕駛員座椅底板處的加權加速度均方根值，而不是座椅上表面的加權加速度均方根值，考慮到人體——座椅系統對加速度有進一步的衰減，實際的整車平順性還要好一些。

8 結 論

利用多體動力學軟件ADAMS建立整車的兩種不同模型，通過對所建立模型在兩種不同駕駛室懸置情況下的仿真分析與比較，得到了兩種模型在行駛平順性分析中的差異，發現剛柔耦合模型的平順性更好。但是，在實際汽車設計研發中，又要求駕駛室具有一定的剛度來滿足相關性能要求，這就需要對駕駛室做更深入研究，以便選擇合適的駕駛室剛度，來實現更好的整車性能。以上仿真分析結果對整車平順性的進一步深入分析起到一定的指導作用，也為駕駛室的設計開發提供參考，為下一步的分析研究打下了良好的基礎。

[1]雷啟明. 輪胎均勻性對牽引車行駛平順性影響試驗研究 [J].汽車科技. 2011, (3)：62-66.

[2]Odilon T Perseguim, A Costa Neto. Comfort and vibration study of atractor and trailer combination using simulation and experimental approaches：the jumping ride behavior[C]. SAE Paper 2000013517, 2000.

[3]王登峰，郝赫，劉盛強，等. 車架彈性對重型載貨汽車行駛平順性的影響 [J]. 農業機械學報，2010, 41 (12)：7-11.

[4]Patricio P S’Ahmadian M. Dynamic influence of frame stiffness on heavy truck ride evaluation［C］.SAE Paper，2004-01-2623.

[5]雷良育, 周曉軍. 基于虛擬樣機技術的汽車平順性仿真分析[J]. 傳感技術學報, 2646-2649.

[6]郭立群, 王登峰. 車架剛度對商用車乘坐舒適性的影響[J]. 吉林大學學報：工學版, 2010, 40（4）：911-914.

[7]Ibrahim I M’Crolla D A’Barton D C. Effect of frame flexibility on the ride vibration of trucks［J］. Computers＆ Structures, 1996, 58（4）：709-713.

[8]D E Newland. General liner Theory of Vehicle Response to Random Road Roughness, 2002.

[9] GB/T 4970-1996 汽車平順性隨機輸入行駛試驗方法[S]. 北京：中國標準出版社, 1996：197-203.

[10]余志生. 汽車理論第4版. [M]. 北京：機械工業出版社, 2008, 5.

[11]李惠彬, 劉亞彬, 上官云飛. 基于ADAMS的重型貨車汽車平順性仿真研究[J]. 重型汽車, 2007, 12（6）：10-12.

[12]熊飛. 以剛彈耦合模型為基礎的運動車平順性仿真分析[J].現代制造工程, 2010, (5)：53-57.