數值試驗模擬邊坡動力響應

趙錫森 粟海濤 張 森

(1.昆明繞城公路西北段建設指揮部，云南昆明 650051;2.云南省公路科學技術研究院，云南昆明 650051)

0 引言

地震狀況下邊坡的穩定性與安全性相當重要，由于地震作用于邊坡的特殊性和復雜性，依靠室內儀器所做試驗都是利用振動臺模型試驗，但此類試驗要求的硬件、軟件設施較高，國內外關于室內模擬地震作用下的邊坡動力響應相關報道很少。對實體工程進行現場觀測較難，且不能大規模的推廣，加之由于地震的區域性較少的監測數據，不能給廣泛的工程提供可靠指導，所以依賴于數值分析的手段進行計算與評價，是人們首選的途徑，加上現在巖土工程界的軟件成熟，使數值模擬成為一種輔佐人們進行工程活動的重要工具，進而人們提出了相對于室內儀器試驗的數值試驗。

隨著我國西部大開發戰略的實施，一批重大工程相繼開工建設。由于西部地區受青藏高原隆升的影響，地形變化大，地質構造復雜，在工程建設中不免有高邊坡產生［1］，而西部又是地震多發區，不少學者和專家對地震邊坡做了一些研究［2-5］，對于巖質邊坡動力響應規律的研究具有重大意義。

1 巖質邊坡動力分析模型

1)材料模型。本文著重研究坡高和坡度對邊坡動力響應的影響，因此將巖石邊坡概化為均質、連續的彈塑性模型，巖體的物理力學參數采用文獻［5］中的參數，如表1所示。

表1 邊坡巖體物理力學參數

2)地震波的選取。動載荷是截取1995年日本的Kobe地震波中具有代表性的一段，峰值加速度為0.83 m/s2，時間步長為0.02 s，如圖1所示。

3)模擬工況。所研究的邊坡高度變化從50 m，100 m，200 m到300 m，具體工況如圖2，表2所示。

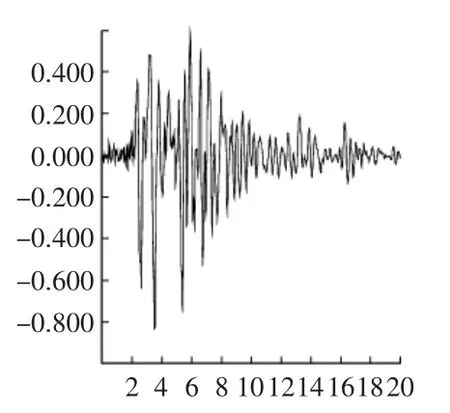
圖1 水平加速度—時間記錄

圖2 巖質邊坡簡化模型

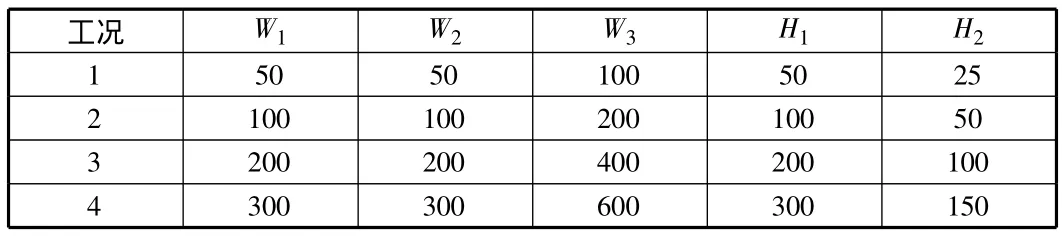
表2 不同工況下邊坡的幾何特征 m

2 模態分析

在ANSYS軟件中，模態分析用于確定結構的固有頻率和振型，同時也是其他動力學分析問題的一個必要步驟。在邊坡的有限元模型建立之后，用分塊Lanczos法進行模態分析，求出系統的前10階振型和頻率，如表3所示。

從表3可以得出以下結論:

1)自振頻率與坡高成反比，當H1＜200 m時，其自振頻率隨階數的減小降低的較快;當H1＞200 m時減小的較慢。

表3 不同工況下邊坡的自振頻率 Hz

2)從圖3中可以看出，高邊坡自振頻率較小、周期大，可以看出高邊坡對頻率大周期短的地震波反應遲鈍，低邊坡由于自振頻率大，周期短，易于頻率短的地震波發生共振，動力響應強烈。

3 動力響應時程分析

本文主要考慮監測點A，B，C三點X方向位移和加速度在地震作用下的響應規律。

圖4～圖7分別為50 m，100 m，200 m，300 m坡高所對應的坡腳、坡腰和坡頂三點的水平位移時程曲線。其中深灰曲線為坡頂(對應圖2中C點)的水平位移和加速度時程曲線，淺灰曲線為坡腰(對應圖2中B點)的水平位移和加速度時程曲線，黑色曲線為坡腳(對應圖2中A點)的水平位移和加速度時程曲線。

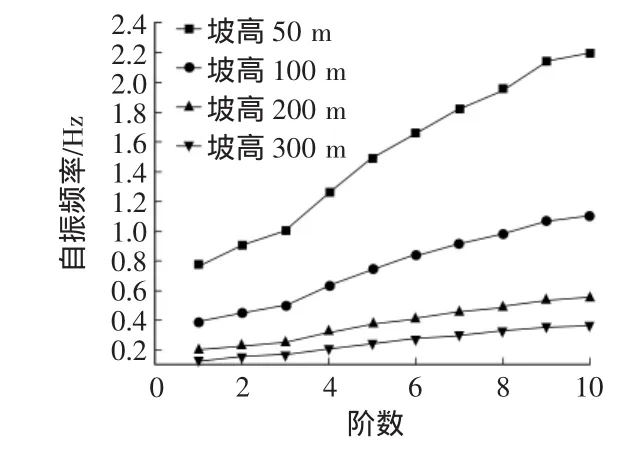
圖3 自振頻率與階數的關系曲線

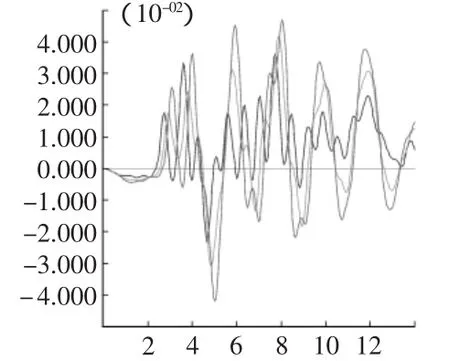
圖4 50 m坡高A，B，C三點X方向位移時程曲線

圖5 100 m坡高A，B，C三點X方向位移時程曲線

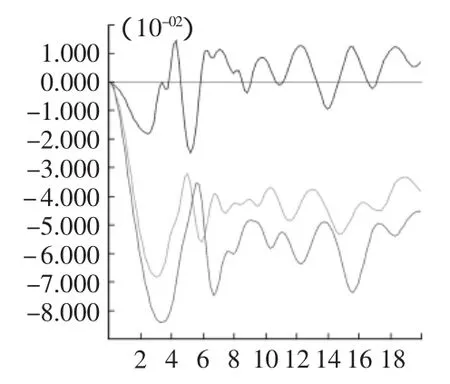
圖6 200 m坡高A，B，C三點X方向位移時程曲線

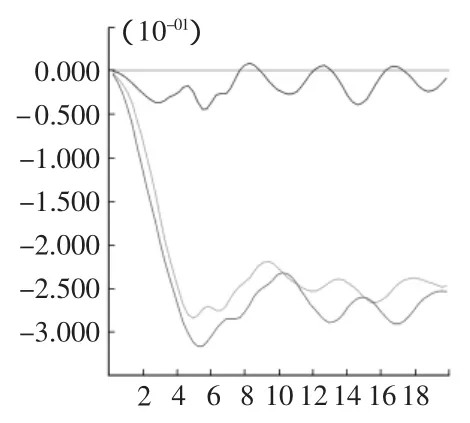
圖7 300 m 坡高A，B，C三點X方向位移時程曲線

從數值模擬的結果圖4～圖7可以看出，不同坡高下巖質邊坡的監測點X方向位移有以下特點:

1)在地震波輸入的開始階段，監測點的位移曲線存在明顯的滯后效應，監測點A，B，C在地震波持時約6 s時，X方向位移速度保持一致方向。這是因為地震波在邊坡中從坡底到坡頂需要一段時間T，T與坡的自振頻率、坡高、地震波的性質有關。

2)從圖4，圖5可以看出，在邊坡較低時，監測點的X方向位移能較快的保持一致，坡面上各點的位移相差不大。從圖6，圖7可以看出，監測點的位移相差較大，當邊坡高為200 m在持時20 s時間段內，最大相差約0.06 m，而當邊坡高為300 m時，監測點位移最大差值減小為0.03 m，這又是由于地震波在傳播的過程中，由于傳播介質的阻尼存在，衰減效應開始顯現造成的。

3)從圖4～圖7中可以發現坡頂的位移是最大的(深灰線表示)，這說明地震波在邊坡傳播過程中存在放大效應。對于同一種地震波，隨邊坡高度增加，坡肩在X向位移相對的坡腳處的相對位移增大，但絕對位移沒有反映出這個規律。

從數值模擬的結果圖8～圖11可以看出，不同坡高下巖質邊坡的監測點X方向位移有以下特點:

1)從四種工況不同坡高監測點來看，輸入地震波最大的峰值加速度為0.83 m/s2，但在地震作用持時20 s時間內，監測點最大峰值加速度為0.75 m/s2，由此可看出地震波在巖土體中傳播具有衰減效應。

2)有些文章中描述三量放大系數，定義為邊坡地震動力反應三量的波動峰值與坡腳三量波動峰值的比值。通過本數值模擬認為不妥，動力三量在邊坡不同監測點是隨時間時刻變化，監測點動力三量與坡腳的動力三量不是在同一時刻取到波動峰值，即三量放大系數是在地震作用過程中，提取整個過程中的三量峰值，最后繪制三量放大系數等值線，也就是同一放大系數不具有同時性，根據現在工程的信息化、動態化要求，要建立同一時刻的三量放大效應時程等值線較目前的三量放大系數等值線有意義。

3)從圖8～圖11可以看出，當地震波在邊坡體內傳播穩定以后，坡肩處的地震加速度最大，坡肩處動力響應強烈。

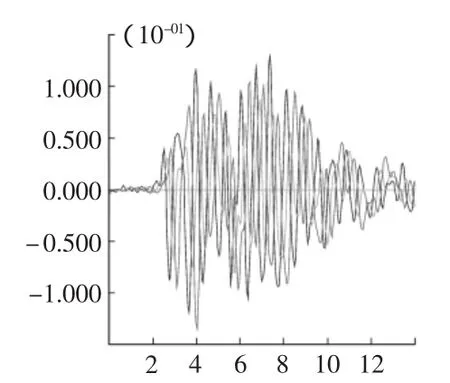
圖8 50 m坡高A，B，C三點X方向加速度時程曲線

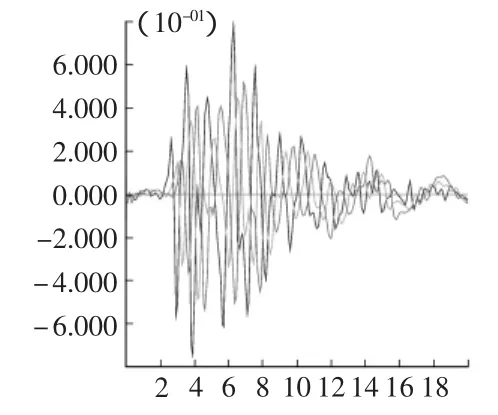
圖9 100 m坡高A，B，C三點X方向加速度時程曲線

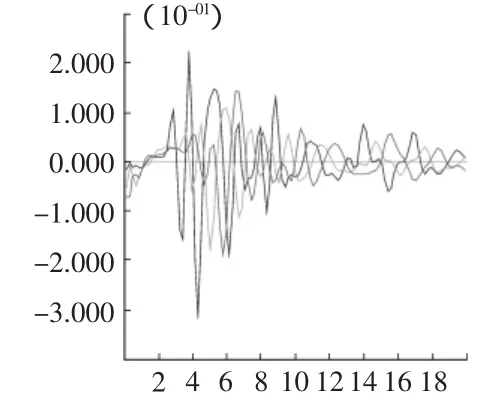
圖10 200 m 坡高A，B，C三點X方向加速度時程曲線

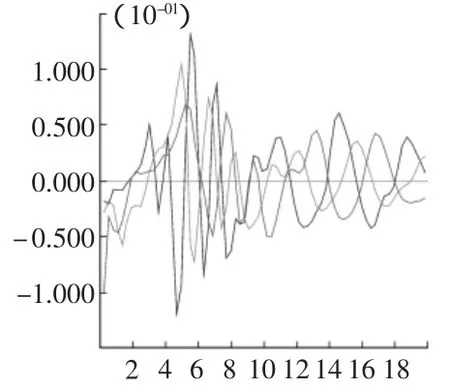
圖11 300 m坡高A，B，C三點X方向加速度時程曲線

4 結語

文章從四種工況出發，首先從不同工況的自振頻率研究入手，對同一地震波不同監測點的動力響應分析進行統計分析得到以下結論:1)隨坡高的增加，邊坡的自振頻率減小，高頻地震波對低邊坡影響較大，低頻地震波對高邊坡的影響較大。2)提出目前眾文章中的動力反應三量放大系數等值線的缺陷，提出建立同一時刻的三量放大效應時程等值線的思路。3)指出地震波在邊坡體傳播中存在滯后效應和放大效應。對于同一種波，當地震波在巖體內傳播穩定時，X方向位移隨著邊坡高度的增加，坡肩相對坡腳的相對位移變大，但絕對位移未表現出這個規律。4)地震波在傳播過程中的衰減效應與邊坡對其的放大效應是同時存在的，這兩種效應與地震波的特性和邊坡的性質有關。

［1］李天斌，王蘭生.巖質工程高邊坡穩定性及其控制［M］.北京:科學出版社，2008.

［2］祁生文，伍法權，嚴福章，等.巖質邊坡動力反應分析［M］.北京:科學出版社，2007.

［3］徐光興，姚令侃，李朝紅，等.邊坡地震動力響應規律及地震動參數影響研究［J］.巖土工程學報，2008，30(6):918-923.

［4］秋仁東，石玉成，付長華.高邊坡在水平動荷載作用下的動力響應規律研究［J］.世界地震工程，2007，23(2):131-138.

［5］梁 力，王 偉，李 明.某露天礦巖質高邊坡地震動力響應及穩定性分析［J］.金屬礦山，2008(8):20-25.

［6］陳國興，莊海洋，杜修力，等.土—地鐵隧道動力相互作用的大型振動臺試驗——試驗結果分析［J］.地震工程與工程振動，2007，27(1):164-170.

［7］祁生文，伍法權，劉春玲，等.地震邊坡穩定性的工程地質分析［J］.巖石力學與工程學報，2004，23(16):2792-2797.