弱L-平均條件下非精確牛頓型迭代法的半局部收斂性

劉 濤, 徐秀斌, 肖 媛

(浙江師范大學(xué) 數(shù)理與信息工程學(xué)院,浙江 金華 321004)

1001-5051(2012)04-0395-06

弱L-平均條件下非精確牛頓型迭代法的半局部收斂性

劉 濤, 徐秀斌, 肖 媛

(浙江師范大學(xué) 數(shù)理與信息工程學(xué)院,浙江 金華 321004)

主要研究了在弱L-平均條件下非精確牛頓型迭代法在求解非線性算子方程時(shí)的半局部收斂性.這種弱L-平均條件包含了常用的Lipschitz條件作為特殊情形,故所得收斂結(jié)果具有一般性.

非線性算子方程;非精確牛頓型迭代法;半局部收斂;弱L-平均條件

0 引 言

令X和Y是歐氏空間或一般的Banach空間,D是X的一個(gè)開凸子集,設(shè)F:D?X→Y是一個(gè)Fréchet可導(dǎo)的非線性算子,

求解非線性方程(1)的近似解是一個(gè)重要的問題,因?yàn)榇罅康牟煌愋偷膶?shí)際問題都可歸結(jié)為方程(1)的形式,如微分方程、邊界值問題、積分方程等.常常用非精確迭代程序求方程(1)解的問題,它的一般表達(dá)形式為

式(2)中：初始點(diǎn)x0給定；在Rn中A(xk)是一個(gè)n×n的非奇異矩陣;控制序列{ηk}滿足0≤ηk≤1.當(dāng)A(xk)=F′(xk)時(shí),可以得到非精確牛頓型迭代法,其迭代程序?yàn)?/p>

當(dāng)A(xk)=F′(x0)時(shí),可以得到簡化的非精確牛頓迭代法;當(dāng)A(xk)近似于F′(xk)時(shí),就得到了非精確牛頓型迭代法(2)[1].

非精確牛頓迭代法包含了經(jīng)典的牛頓迭代法[2-3],對(duì)于非精確牛頓法殘余序列的選擇影響著非精確牛頓法的收斂性.文獻(xiàn)[4]給出了非精確牛頓法(3)的半局部收斂定理,其中殘余序列{rn}滿足:

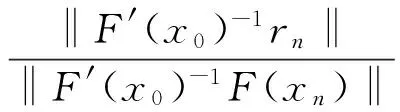
此時(shí)0≤ηn<η< 1.文獻(xiàn)[5]利用Lipschitz條件在開集B(x0,δ)上給出了非精確牛頓迭代法(3)的半局部收斂定理,此時(shí){rn}滿足

‖F(xiàn)′(x0)-1rn‖≤ηn‖F(xiàn)′(x0)-1F(xn)‖1+β,0≤β<1.

文獻(xiàn)[6]利用H?lder條件,在集合B(x0,r)上給出了非精確牛頓迭代法(3)的半局部收斂定理.文獻(xiàn)[7]利用局部弱L-平均條件

在集合B(x0,δ)上給出了非精確牛頓迭代法(3)的局部收斂定理.其中：ρ(x)=‖x-x*‖；xτ=x*+τ(x-x*)(0<τ<1).文獻(xiàn)[8]利用弱L-平均條件

本文主要通過利用弱L-平均條件和控制條件‖F(xiàn)′(x0)-1(rn-rn-1)‖≤ηn‖xn-xn-1‖研究非精確牛頓型迭代法(2)的半局部收斂性,所得結(jié)果比文獻(xiàn)[4,9]的相關(guān)結(jié)論更具有一般性.

1 引 理

根據(jù)本文的需要,首先給出4個(gè)引理及證明,然后在這些引理的基礎(chǔ)上證明迭代方法(2)的半局部收斂性.

在給出收斂定理之前先定義如下2個(gè)輔助函數(shù):

式(4)和式(5)中，L(u)為非負(fù)非減可積的連續(xù)函數(shù).

函數(shù)f(x)和g(x)的導(dǎo)函數(shù)分別為:

則由式(6)和式(7)可以得到

取θ0>0,使得

且記

f(0)=β>0,f(θ0)=-ω2b+β<0,f(R)=β+λR>0.

故f在定義域[0,R]內(nèi)恰有2個(gè)正根,分別記為t*和t**,且有

0

證明 由式(4)知

又由前面給出的條件易得f′(0)<0,f′(θ0)=0,f′(R)>0,故可以得到函數(shù)f(t)在區(qū)間[0,θ0]上單調(diào)遞減,在區(qū)間[θ0,R]上單調(diào)遞增;又因f(θ0)=-ω2b+β<0,故f在區(qū)間[0,R]內(nèi)恰有2個(gè)正根t*和t**,所以有0

引理2設(shè)迭代序列

式(11)中,f(t),g(t)由式(4)和式(5)定義.設(shè)t*是方程f(t)=0在區(qū)間[0,θ0]的一個(gè)根,則由式(11)產(chǎn)生的序列{tn}有

且{tn}單調(diào)遞增收斂到t*,并有

證明 由式(11)可得

下證t1

因此由f的單調(diào)性可知t1=β

現(xiàn)在假設(shè)t10,故有

另一方面,由式(8)可以得到

所以式(12)得證.序列{tn}單調(diào)遞增地收斂于一點(diǎn),記為γ(γ∈[0,t*]),且γ也是方程f(t)=0的一個(gè)根.又由于t*是方程f(t)=0在[0,t*]內(nèi)唯一的一個(gè)根,所以γ=t*,即序列{tn}收斂到t*.

最后證明式(13)成立.由式(8)可以得到

故式(13)成立.引理2證畢.

引理3假設(shè)F′(x0)-1F′在開域B(x0,t*)上滿足

且對(duì)于任意x∈B(x0,t*),F′(x)-1存在,則

證明 由已知可得

則由Banach引理和式(9)易得

故式(18)成立.引理3證畢.

引理4[3]設(shè)

其中0≤ρ≤t*,且L(u)在[0,t*]上非負(fù)遞增,則φ(t)在[0,t*-ρ]上關(guān)于t單調(diào)遞增.

2 半局部收斂性定理

根據(jù)上面的引理,以下給出非精確牛頓型迭代法(2)的半局部收斂性定理.

定理1假設(shè)F:D?X→Y是一階連續(xù)Fréchet可導(dǎo)的非線性算子,D是X的開凸子集.若存在初始點(diǎn)x0∈D,使得F′(x0)-1∈L(Y,X)存在,且有:

A(x)可逆;‖F(xiàn)′(x0)-1(A(x)-F′(x))‖≤ω1;‖A(x)-1F′(x)‖≤ω2.

證明 由非精確牛頓型迭代法的迭代式(2)可以得到

xn+1-xn=-A(xn)-1F(xn)+A(xn)-1rn,n=0,1,…,

所以

‖xn+1-xn‖= ‖A(xn)-1(F(xn)-rn)‖≤

‖A(xn)-1F′(xn)‖‖F(xiàn)′(xn)-1F′(x0)‖‖F(xiàn)′(x0)-1(F(xn)-rn)‖.

(25)

下面用數(shù)學(xué)歸納法證明式(23)和

成立.

當(dāng)k=0時(shí),由式(20)有

‖x1-x0‖=‖A(x0)-1(F(x0)-r0)‖≤β=t1-t0,t0=0.

‖z-x0‖≤‖z-x1‖+‖x1-x0‖≤t*-t1+t1-t0=t*-t0,

下面假設(shè)當(dāng)k=n-1時(shí)結(jié)論成立,即有

其中:xn-1+τ=xn-1+τ(xn-xn-1);0<τ<1.所以由式(21)和式(22)及引理4有

(27)

所以由引理2、引理3及式(25)有

(28)

‖z-xn‖≤‖z-xn+1‖+‖xn+1-xn‖≤t*-tn+1+tn+1-tn=t*-tn.

3 應(yīng) 用

根據(jù)定理1,當(dāng)A(x)=F′(x)時(shí),可以給出非精確牛頓迭代法(3)的半局部收斂性定理.此時(shí)優(yōu)函數(shù)式(4)和式(5)為如下形式:

(29)

定理2假設(shè)F:D?X→Y是一階連續(xù)Fréchet可導(dǎo)的非線性算子,D是X的開凸子集.若存在初始點(diǎn)x0∈D,使得F′(x0)-1∈L(Y,X) 存在,且有

(31)

(32)

(33)

式(34)和式(35)中,{sn}單調(diào)遞增收斂到s*并滿足

當(dāng)令L(u)≡L(這里L(fēng)是一個(gè)大于零的常數(shù))時(shí),由定理2可以得到文獻(xiàn)[4,9]中的相關(guān)結(jié)論.

推論1設(shè)F:D?X→Y在集合B(x0,t*)內(nèi)連續(xù)可導(dǎo),假設(shè)式(22)成立且控制序列{ηk}滿足0≤ηk<1.F′(x0)F′滿足對(duì)于任意的x∈B(x0,t*),‖x-x0‖+‖x-x′‖≤t*時(shí)有

‖F(xiàn)′(x0)(F′(x)-F′(x′))‖≤L‖x-x′‖.

若2βL≤(1-η)2,則由迭代方法(3)產(chǎn)生的序列{xk}收斂到方程(1)的解x*.

[1]Dembtexto R S,Eisenstat S C,Steihaug T.Inexact Newton methods[J].Numer Anal,1982,19(2):400-408.

[2]Kantorvich L V,Akilov G P.Functional analysis[M].Oxford:Pergamon Press,1982.

[3]Wang Xinghua.Convergence of Newton′s method and inverse function theorem in Banach space[J].Math Comput,1999,68(225):169-186.

[4]Guo Xueping.On semilocal convergence of inexact Newton methods[J].Comput Math,2007,25(2):231-242.

[5]Argyros I K,Ren Hongmin.Kantorovich-type semilocal convergence analysis for inexact Newton methods[J].Comput Appl Math,2011,235(9):2993-3005.

[6]Shen Weiping,Li Chong.Convergence criterion of inexact Newton methods for operators with H?lder continuous derivatives[J].Taiwanese Journal of Math,2008,12(7):1865-1882.

[7]Chen Jinhai,Li Weiguo.Convergence behaviour of inexact Newton methods under weak Lipschitz condition[J].Comput Appl Math,2006,191(5):143-164.

[8]Wu Min.A new semilocal convergence theorem for the inexact Newton methods[J].Appl Math Comput,2008,200(1):80-86.

[9]Argyros I K.On the semilocal convergence of inexact Newton methods in Banach spaces[J].Comput Appl Math,2009,228(9):434-443.

SemilocalconvergenceofinexactNewton-typeiterationmethodsunderweakL-averagecondition

LIU Tao, XU Xiubin, XIAO Yuan

(CollegeofMathematics,PhysicsandInformationEngineering,ZhejiangNormalUniversity,JinhuaZhejiang321004,China)

The semilocal convergence properties of the variants of inexact Newton-type iteration methods for nonlinear operator equations were studied under the hypothesis that the first derivative satisfies weakL-average conditions. These conditions included the usual Lipschitz condition as special cases.

nonlinear operator equations; inexact Newton-type iteration method; semilocal convergence; weakL-average condition

2012-04-10

劉 濤(1987-)，男,河南固始人,碩士研究生.研究方向:非線性數(shù)值逼近.

O241

A

(責(zé)任編輯 陶立方)