活動(dòng)標(biāo)架在對(duì)象識(shí)別中的應(yīng)用＊

姚若俠，袁 偉，成麗美

(陜西師范大學(xué) 計(jì)算機(jī)科學(xué)學(xué)院，陜西 西安 710062)

0 引言

19 世紀(jì)早期，法國數(shù)學(xué)家Cartan［1-2］融合了Darboux，F(xiàn)renet，Serret 和Cotton 的早期工作，提出并發(fā)展了活動(dòng)標(biāo)架理論的現(xiàn)代方法，其核心工作是將活動(dòng)標(biāo)架轉(zhuǎn)變?yōu)橐环N強(qiáng)大的計(jì)算工具，并借助該方法分析子流形的幾何性質(zhì)和變換群作用下的微分不變量.20 世紀(jì)70 年代，研究人員［3-5］開始試圖將Cartan的直觀構(gòu)造方法歸納為堅(jiān)實(shí)的理論基礎(chǔ).近年來，F(xiàn)els 等［6-7］擺脫了狹隘的框架束縛，建立了一個(gè)新的、強(qiáng)大的、具有建設(shè)性的方法，該新方法定義活動(dòng)標(biāo)架為一個(gè)從子流形或者Jet 叢(射流叢)到群變換的等變映射.這一定義的給出引發(fā)了一個(gè)極其重要的概念上的跳躍，從而將活動(dòng)標(biāo)架理論從對(duì)任何形式標(biāo)架叢或聯(lián)絡(luò)的依賴中分離出來.該方法可被系統(tǒng)地應(yīng)用于一般變換群，且所有經(jīng)典的活動(dòng)標(biāo)架都可以用這種方法重新詮釋.

Cartan 的活動(dòng)標(biāo)架規(guī)范化構(gòu)造方法的關(guān)鍵點(diǎn)就是要相對(duì)于群軌道選擇若干橫截面，這樣就可以通過規(guī)范化系統(tǒng)的選定構(gòu)造等變活動(dòng)標(biāo)架，并通過誘導(dǎo)的不變化過程產(chǎn)生不變量的完備系.理論上，活動(dòng)標(biāo)架存在的必要條件是群作用必須是自由的.經(jīng)典地，對(duì)于非自由的群作用，可以將它延拓到Jet 空間構(gòu)造基本微分不變量和高階微分不變量［8］.

現(xiàn)代圖像處理的首要目標(biāo)就是在不同方向、不同位置，甚至有某些形變的情形下去識(shí)別這些對(duì)象.在識(shí)別過程中，目標(biāo)對(duì)象首先需要用其邊界輪廓曲線去表示.若已知一個(gè)變換群作用，我們的任務(wù)就是要確定2 個(gè)對(duì)象是否能夠通過一個(gè)變換相互映射，也就是說，2 個(gè)對(duì)象的邊界曲線在群作用下能否匹配.實(shí)際上，這一匹配問題，或者說輪廓曲線的重疊問題就約化為邊界曲線的對(duì)稱分類問題.受到Cartan關(guān)于等價(jià)問題解［9］和活動(dòng)標(biāo)架的等變映射方法的啟發(fā)，Calabi［10］提出了微分不變簽名曲線，它由曲率和曲率關(guān)于弧長的導(dǎo)數(shù)這2 個(gè)不變量參數(shù)刻畫.在歐幾里得群變換下，任意曲線都能被簽名曲線唯一描述，也就是說，平面上的任意一條曲線，它的簽名曲線不會(huì)因?yàn)榍€的平移和旋轉(zhuǎn)而發(fā)生改變.因此，簽名曲線能很自然地應(yīng)用于計(jì)算機(jī)對(duì)象識(shí)別領(lǐng)域.與傳統(tǒng)的方法相比，簽名曲線的曲率和曲率關(guān)于弧長導(dǎo)數(shù)的刻畫方式在對(duì)象識(shí)別中扮演著重要角色，它避免了曲線初始點(diǎn)選擇的影響，消除了曲線重新參數(shù)化的計(jì)算困難，并且很容易被擴(kuò)展到空間曲面和更高維的子流形上［11］.

1 等變活動(dòng)標(biāo)架和微分不變量

1.1 等變活動(dòng)標(biāo)架

一般來說，群G 作用于空間M 和N 上，若存在一個(gè)映射φ:M→N，滿足φ(g·z)→g·φ(z)，對(duì)?g∈G，z∈M 都成立，則φ 是左等變映射.類似地，若滿足φ(g·z)→φ(z)·g-1，則稱φ 為右等映射.

定義1 給定作用在流形M 上的變換群G，則活動(dòng)標(biāo)架是一個(gè)光滑的G 等變映射

定義2 給定一個(gè)光滑的映射ρ:M→G，對(duì)?g∈G，z∈M，若ρ(g·z)→g·ρ(z)，則ρ=ρ(z)是一個(gè)左G 等變映射;若ρ(g·z)→ρ(z)·g-1，則ρ 是一個(gè)右G 等變映射.一個(gè)左(右)活動(dòng)標(biāo)架是一個(gè)左(右)G 等變映射.

定理1 活動(dòng)標(biāo)架在點(diǎn)x∈M 的一個(gè)鄰域內(nèi)存在，當(dāng)且僅當(dāng)G 在點(diǎn)x 附近的作用是自由和正則的.對(duì)?x∈M，g∈G，函數(shù)F:M→G 是一個(gè)G 不變的函數(shù)，則

定義3 對(duì)?x∈M，g∈G，若I(g·x)=I(x)，則實(shí)值函數(shù)I:M→R 是群G 的不變量.若存在單位元e∈G 的一個(gè)鄰域N，對(duì)?x∈U，g∈N，使得I(g·x)=I(x)，則實(shí)值函數(shù)I:U?M→R 是局部不變量.

1.2 活動(dòng)標(biāo)架的構(gòu)造

若已知一個(gè)正則的群作用，則基于Cartan 的規(guī)范化方法［12-13］，便可獲得該群的一個(gè)基本不變量完備集，該方法幾乎完全依賴于橫截面的選取.

定義4 群G 正則作用于m 維流形M，其軌道為s 維，一個(gè)截面是流形M 的m -s 維子流形K，且K 與每個(gè)軌道都恰好橫截于一個(gè)點(diǎn).

定理2 設(shè)群G 自由且正則地作用于流形M 上，K 為一個(gè)截面.給定z∈M，設(shè)g=ρ(z)是唯一一個(gè)將z 映射到截面K 上的群元素:g·z=ρ(z)·z∈K，則ρ:M→G 是該作用的一個(gè)右活動(dòng)標(biāo)架.

給定M 上的局部坐標(biāo)x=(x1，x2，…，xm)，變換群G 的群參數(shù)g=(g1，g2，…，gr)，下面介紹規(guī)范化方法，這是活動(dòng)標(biāo)架方法的核心內(nèi)容.

假設(shè)G 正則地作用于M，為簡單起見，就G 本身而言，假定它的軌道維數(shù)相同且都為r.也就是說，假定G 作用是局部自由的，那么構(gòu)造活動(dòng)標(biāo)架和不變量的主要步驟為:

第2 步:在實(shí)數(shù)集R 上恰當(dāng)?shù)剡x擇r 個(gè)常數(shù)，即c1，c2，…，cr∈R，令坐標(biāo)變換等于這些常數(shù)，即得規(guī)范化方程組

第3 步:對(duì)于群參數(shù)集g=(g1，g2，…，gr)，求解規(guī)范化方程組，即得到群參數(shù)用局部坐標(biāo)表示的形式.若方程組的解

是一個(gè)光滑映射，則式(2)是一個(gè)右活動(dòng)標(biāo)架.

第4 步:計(jì)算其他坐標(biāo)在已獲得的活動(dòng)標(biāo)架下的作用，可得局部不變量的基本完備集

特別地，在第3 步中，常數(shù)可以任意選擇，但有些情況不能選為0，這需視具體情況而定.除此之外，參數(shù)的選擇必須要使這個(gè)正規(guī)化方程組的解存在，這些常數(shù)定義了一個(gè)截面.為了簡化計(jì)算過程，參數(shù)的選擇應(yīng)盡可能地使這些常數(shù)為0 或者1.值得注意的是，假定群變換參數(shù)為r 個(gè)，則選擇一個(gè)橫截面K，使得K={x1=c1，x2=c2，…，xr=cr}.所以，活動(dòng)標(biāo)架即是將點(diǎn)x 映射到由橫截面K 和經(jīng)過點(diǎn)x 的軌道的交點(diǎn)的變換.

定理3 給定一個(gè)自由且正則的群作用和一個(gè)坐標(biāo)截面，設(shè)g=ρ(z)為正規(guī)化方程組的解.若g 是一個(gè)光滑映射，則活動(dòng)標(biāo)架和方程

組成了一個(gè)與群作用的函數(shù)無關(guān)的局部不變量完備系.

1.3 微分不變量及其構(gòu)造

定義5 令G 是一個(gè)點(diǎn)變換或者切變換群.微分不變量是一個(gè)實(shí)值函數(shù)I:Jn→R，對(duì)于所有的z(n)=(x，u(n))，滿足I(g(n)·(x，u(n)))=I(x，u(n)).其中:Jn=Jn(M，p)是n 階擴(kuò)展的Jet 叢;p ＜m(m 是流形M 的維數(shù)).特別地，J0=M，g(n)·(x，u(n))是延拓變換群.

一個(gè)n 階的活動(dòng)標(biāo)架ρ(n):Jn→G 是定義在Jet 空間的開子集上的等變映射，只要n 足夠大，延拓群G(n)在稠密開子集vn?Jn上是正則且自由的.

定理4 n 階活動(dòng)標(biāo)架在點(diǎn)z(n)∈Jn的一個(gè)鄰域內(nèi)存在當(dāng)且僅當(dāng)z(n)∈v(n)是正則的.

考慮作用于平面曲線u=u(x)上的特殊歐幾里得群SE(2):

該群作用的一階延拓定義了一個(gè)作用于J1(R2，1)的自由群

這里，通過選擇一個(gè)好的橫截面{x=0，u=0，ux=0}可獲得J1(R2，1)上的一個(gè)活動(dòng)標(biāo)架.求解對(duì)應(yīng)的規(guī)范化方程組X=U=UX=0，得到右活動(dòng)標(biāo)架

延拓群作用到Jm并取規(guī)范化常參數(shù)，可以獲得m 階的基本微分不變量集.簡單地，取m=3，計(jì)算可得:

將式(3)分別代入式(4)和式(5)，可得基本微分不變量

2 數(shù)值不變簽名曲線

定義6 在平面上，若定義了G 的不變曲率κ 和它的關(guān)于弧長的導(dǎo)數(shù)，且它們是解析的，則曲線C是G 規(guī)則的.

定義7 非退化的規(guī)則平面曲線的G 不變簽名曲線S 由κ 和κs參數(shù)化，即

定理5 一般的r 維變換群G 作用于R，在群G 作用下，當(dāng)且僅當(dāng)2 個(gè)G 規(guī)則的非退化解析曲線C和C 的簽名曲線是相同的，即S=S 時(shí)，它們是等價(jià)的.

在實(shí)際應(yīng)用中，可以通過離散的數(shù)值逼近來計(jì)算微分不變量.一個(gè)魯棒且高效的數(shù)值方法是解決問題的關(guān)鍵所在，但是許多重要的微分不變量階數(shù)比較高，對(duì)舍入誤差和噪音很敏感.為了解決這個(gè)難題，本文使用聯(lián)合不變量為κ，κs找到數(shù)值表達(dá)式，以期獲得不敏感的逼近.

特別地，在子流形中，任何離散的逼近方案最終都將依賴于網(wǎng)點(diǎn)或者離散點(diǎn)的引入，然后，構(gòu)造網(wǎng)點(diǎn)坐標(biāo)的特定結(jié)合，這些網(wǎng)點(diǎn)將會(huì)逼近微分不變量的值.由于變換群下的逼近是不變的，因此，微分不變量的數(shù)值不會(huì)受到群作用的影響.一般地，若G 是一個(gè)作用于空間E 上的群，則聯(lián)合不變量［14］是依賴于有限個(gè)點(diǎn)x1，x2，…，xn的函數(shù)J(x1，x2，…，xn).從點(diǎn)的配置上看，這些點(diǎn)在群元素g∈G 的同步作用下是保持不變的.例如，對(duì)于歐幾里得群，聯(lián)合不變量是點(diǎn)P，Q 之間的歐幾里得距離d(P，Q)的函數(shù).類似地，對(duì)于等仿射群，給定三角形的3 個(gè)頂點(diǎn)P，Q，R，最簡單的結(jié)合不變量就是三角形的面積A(P，Q，R)，也就是說，每個(gè)聯(lián)合不變量是這些三角形面積的函數(shù).Green［4］的研究結(jié)果給出了曲線的微分不變量個(gè)數(shù)和群作用的聯(lián)合不變量的個(gè)數(shù)之間的關(guān)聯(lián)，用于形成更實(shí)際的聯(lián)系，建立了離散的和連續(xù)的不變理論的橋梁［15］.因此，使用一個(gè)有限差分逼近方法為一個(gè)微分不變量I 構(gòu)造數(shù)值逼近，以便用網(wǎng)點(diǎn)坐標(biāo)的結(jié)合來計(jì)算這個(gè)逼近.于是，任何對(duì)于微分不變量的G 不變數(shù)值逼近一定會(huì)由G 的聯(lián)合不變量的一個(gè)函數(shù)控制.我們將通過平面上的歐幾里得曲線詳細(xì)介紹數(shù)值不變簽名曲線的求解過程.

對(duì)于包含了旋轉(zhuǎn)和平移變換的特殊歐幾里得群SE(2)，依據(jù)Weyl［16］的方法，歐幾里得群的每個(gè)聯(lián)合不變量都是歐幾里得距離d(P，Q)=|P-Q|的函數(shù)和位移向量之間的交乘(P -Q)∧(R -S).對(duì)于一個(gè)規(guī)則，光滑的平面曲線C，其歐幾里得群最簡單的微分不變量是歐幾里得曲率κ.曲線在點(diǎn)P∈C 處的曲率的絕對(duì)值是其內(nèi)切圓半徑的倒數(shù).通常，若曲線的方程為u=u(x)，且u(x)具有二階導(dǎo)數(shù)，則曲線u=u(x)在點(diǎn)(x，u(x))處的曲率為

對(duì)于凸曲線，曲率是正的;反之，凹曲線的曲率是負(fù)的.

從定理6 可以看出，盡管曲線關(guān)于弧長的連續(xù)導(dǎo)數(shù)導(dǎo)致無限多個(gè)更高階微分不變量，但是只需要考慮前2 個(gè)微分不變量κ 和κs就能夠完全刻畫曲線.

接下來，用聯(lián)合不變量逼近微分不變量來說明本節(jié)討論的理論體系，描述如何用標(biāo)準(zhǔn)的幾何構(gòu)造來獲得一個(gè)數(shù)值逼近.當(dāng)然，對(duì)于歐幾里得曲率，因其在剛體運(yùn)動(dòng)下不受影響，故曲線的任何平移或旋轉(zhuǎn)運(yùn)動(dòng)都有相同的數(shù)值逼近.鑒于歐幾里得聯(lián)合不變量的特征，迫使這個(gè)逼近只能依靠網(wǎng)點(diǎn)間的距離來實(shí)現(xiàn).此外，因?yàn)榍适嵌A微分函數(shù)，所以要求取3 個(gè)網(wǎng)點(diǎn)來逼近.

圖1 曲率逼近

由于式(6)僅依賴于點(diǎn)之間的距離，所以，對(duì)于曲線L 上的中間點(diǎn)B，它給出了該點(diǎn)曲率的完整的歐幾里得不變數(shù)值逼近.

同樣的方法也可用于逼近高階微分不變量κs，則κs在點(diǎn)Pi處的有限差商表達(dá)式為

由于選擇的點(diǎn)不是對(duì)稱的，因而導(dǎo)致了數(shù)值偏差，所以要選取的點(diǎn)必須是對(duì)稱的，從而κs的中心差商表達(dá)式為

這樣，要想獲得簽名曲線的歐幾里得不變離散逼近，必須使用(κ(Pi-1，Pi，Pi+1)，κs(Pi-2，Pi-1，Pi，Pi+1，Pi+2))作為要逼近的點(diǎn).

3 例證結(jié)果與分析

為了簡單地說明曲線的數(shù)值不變簽名曲線的求解問題，筆者選取了2 個(gè)具有函數(shù)表達(dá)式的曲線，當(dāng)然，這個(gè)方法可以用于任何曲線.通過離散化極坐標(biāo)上的角度來實(shí)現(xiàn)曲線上點(diǎn)的選取，進(jìn)而使用數(shù)值方法實(shí)現(xiàn)不變簽名曲線的構(gòu)造.

圖4 左側(cè)為極坐標(biāo)方程r2=3 +cos(3θ)的原始曲線圖，右側(cè)為r2的旋轉(zhuǎn)一個(gè)角度后的曲線圖;圖5為圖4 中的2 條曲線的簽名曲線，左圖為連續(xù)曲線，右圖為離散曲線.由于旋轉(zhuǎn)比平移稍復(fù)雜一些，本文以旋轉(zhuǎn)為例來說明剛體變化.可以看出:盡管曲線發(fā)生了剛體變化(如平移、旋轉(zhuǎn))，但它的簽名曲線是一樣的.由此可見，任何發(fā)生剛體變化的對(duì)象都可以通過它們的簽名曲線來分類和識(shí)別.也就是說，只要對(duì)象的簽名曲線是相同的，那么它們就是同一個(gè)對(duì)象.

圖2 r1=的連續(xù)原始曲線和離散原始曲線

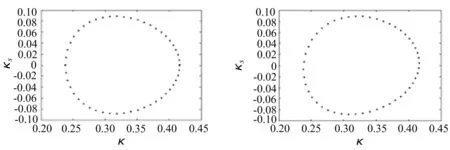
圖3 有偏差和無偏差的離散簽名曲線

圖4 r2=3 +cos(3θ) 的原始曲線和旋轉(zhuǎn)一個(gè)角度后的曲線

圖5 連續(xù)和離散的簽名曲線

4 結(jié)語

在計(jì)算機(jī)對(duì)象識(shí)別中，可以將對(duì)象的輪廓提取出來，方法之一就是將對(duì)象識(shí)別的問題轉(zhuǎn)化為曲線的識(shí)別問題.在實(shí)際應(yīng)用中，被識(shí)別的對(duì)象可能會(huì)由于某種原因發(fā)生了旋轉(zhuǎn)和平移變化，甚至某種程度上的扭曲(仿射變化)，導(dǎo)致對(duì)象難以識(shí)別.使用簽名曲線可以很好地解決這個(gè)問題，因?yàn)槿我馇€的簽名曲線唯一地刻畫了這個(gè)曲線，且不會(huì)隨著對(duì)象的旋轉(zhuǎn)和平移發(fā)生變化.對(duì)于仿射變化，可以用同樣的數(shù)值方法進(jìn)行仿射逼近來獲得其簽名曲線.與剛體變化所得的結(jié)論一樣，對(duì)象的簽名曲線不會(huì)隨著對(duì)象的仿射變化而發(fā)生變化，所以可以通過比較簽名曲線而不是比較曲線本身來獲知曲線是否匹配，這在很大程度上降低了識(shí)別的復(fù)雜度.

［1］Cartan é.La méthode du Repére mobile，la théorie des groupes continus，et les espaces généralisés，exposés de géométrie［M］.Paris:Hermann，1935.

［2］Cartan é.La théorie des groupes finis et continus et la géométrie différentielle traitées par la méthode du repére mobile［M］.Paris:Gauthier-Villars，1937.

［3］Griffiths P.On Cartan′s method of Lie groups as moving frames as applied to uniqueness and existence questions in differential geometry［J］.Duke Math J，1974，41(4):775-814.

［4］Green M L.The moving frame，differential invariants and rigidity theorems for curves in homogeneous spaces［J］.Duke Math J，1978，45(2):735-779.

［5］Jensen G R.Higher order contact of submanifolds of homogeneous spaces［M］.New York:Springer-Verlag，1977.

［6］Fels M，Olver P J.Moving coframes I:A practical algorithm［J］.Acta Appl Math，1998，51(2):161-213.

［7］Fels M，Olver P J.Moving coframes II:Regularization and theoretical foundations［J］.Acta Appl Math，1999，55(2):127-208.

［8］Olver P J.Generating differential invariant［J］.Math Anal Appl，2007，333(1):450-471.

［9］Olver P J.Equivalence，invariants，and symmetry［M］.London:Cambridge University Press，1995.

［10］Calabi E，Olver P J，Tannenbaum A.Affine geometry，curve flows，and invariant numerical approximations［J］.Adv In Math，1996，124(1):154-196.

［11］Hoff D J，Olver P J.Extensions of invariant signatures for object recognition［J/OL］.J Math Imaging Vis，2012，DOI:10.1007/s10851-012-0358-7.

［12］Killing W.Erweiterung der begriffes der invarianten von transformationgruppen［J］.Math Ann，1890，35:423-432.

［13］Weiss I.Geometric invariants and object recognition［J］.Int J Comp Vision，1993，10(3):207-231.

［14］Olver P J.Joint invariant signatures［J］.Found Comp Math，2001，1(1):3-68.

［15］Sturmfels B.Algorithms in invariant theory［M］.New York:Springer-Verlag，1993.

［16］Weyl H.Classical Groups［M］.Princeton:Princeton Univ Press，1946.