基于粒子群算法的大型風力機槳距調節計算
楊從新,呂小靜,童 剛
(蘭州理工大學 能源與動力工程學院,甘肅 蘭州730050)
0 引 言
一般風力機風輪的氣動外形是根據給定的額定風速與轉速進行設計的,以保證其以最優的氣動性能產生額定出力[1-2]。然而風電場的風速很少能保持為其額定值,為使風力機風輪在非額定風速下運行時還能具有盡可能高的氣動性能,并且限制其過載運行,就必須使葉片安放角根據風速信號按確定方式調整,即進行槳距調節。
目前,國內的大型風力發電機組多采用統一變槳距控制技術[3],其控制原理如圖1所示。給定風速信號和功率信號,控制系統將按預先設計好的風速與槳距角的對應關系進行控制調節。
為了能夠較準確地進行變槳距調節,本文將采用基于有限葉片變環量的氣動模型,結合粒子群算法對大型風力機的槳距調節進行氣動設計的研究。

圖1 槳距調節控制圖Fig.1 Chart of the pitch adjusting control
1 氣動計算模型的選擇
風力機氣動理論從Betz和Glauert建立的經典理論,到目前常用的動量-葉素理論及其修正,這些理論雖易于估算機組初始設計時整機的氣動性能,但因都進行了一些假設和簡化,故對葉片氣動性能計算還不夠準確。為了能夠得到較準確的氣動計算結果,本文采用一種基于有限葉片變環量的氣動模型[4]。
水平軸風力機風輪的尾流可以看成是由復雜旋渦系統組成的。該旋渦系統由三部分組成:位于風輪軸線上的中心渦、沿葉片軸線的變環量附著渦以及從葉片尾緣與葉尖脫落的螺旋狀自由渦層。其模型如圖2所示。
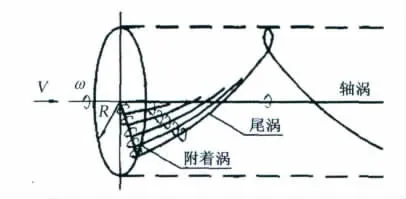
圖2 風輪漩渦氣動模型Fig 2 Aerodynamic vortex model of wind rotor
在上述旋渦系統的基礎上,根據風力機風輪的氣動計算,給出了水平軸風力機風輪的理論模型,即在不作無限葉片數與定環量假設的情況下計算葉片某斷面處的旋渦誘導速度和來流下洗角,給出來流的真實速度大小和方向,用以進行風輪的氣動計算。氣動計算模型圖如圖3。
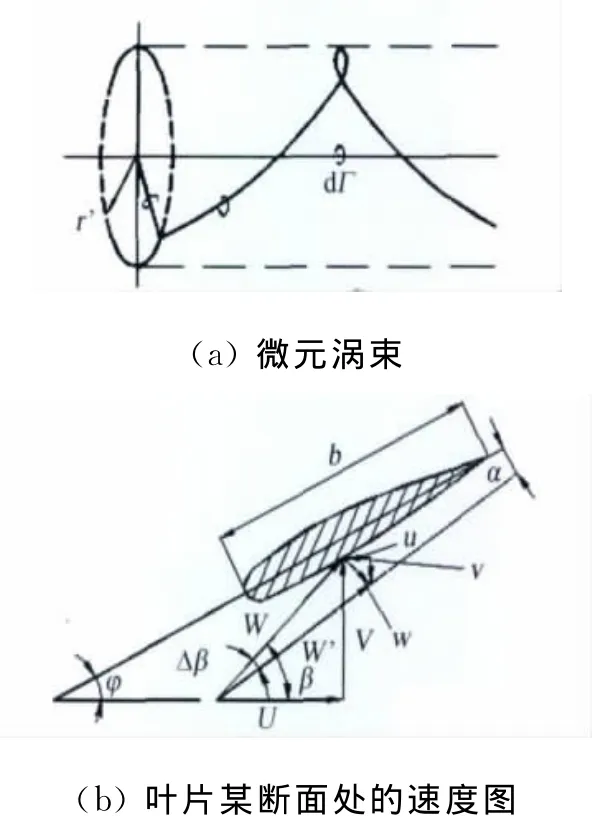
圖3 計算模型圖Fig.3 Calculation models
根據比奧薩法爾定理和庫塔-茹可夫斯基升力公式及翼剖面理論可知,求解環量分布Γ(r)的方程如下:
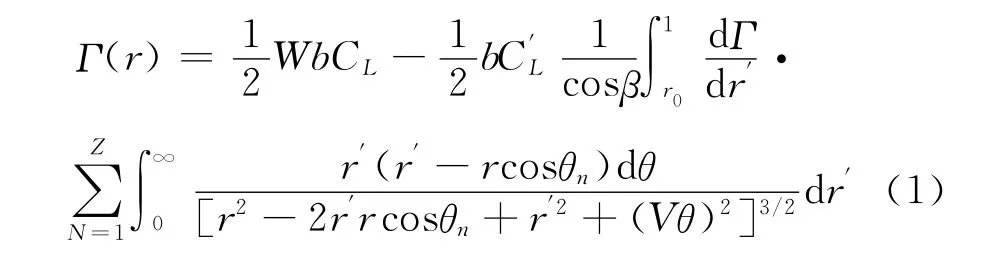
當風輪的來流條件和幾何參數給定后,解此積分微分方程可得到沿槳葉分布的環量和誘導速度及下洗角。進而求得推力系數CF和功率系數CP,其無因次量形式的表達式為 :

式(1)中CL為升力系數,C′L為升力系數對攻角的導數,θn=θl+2π(n-1)/z,θ為中心角,n為葉片斷面數。式(2)中P為功率,F為軸向力,z為葉片數,λ0為葉尖速比,μ為翼型升阻比的倒數。各式中其它參數如圖2和圖3所示[4-7],均為葉片任意斷面位置r的函數,符號上方帶橫線的各參數為其無因次量。
2 粒子群算法簡介
粒子群優化(Particle Swarm Optimization,PSO)算法是近年來發展起來的一種新的進化算法。該算法將從初始化的隨機解出發不斷迭代更新,最終找到最優解。迭代中粒子根據如下兩個公式來更新自己的速度和新的位置:
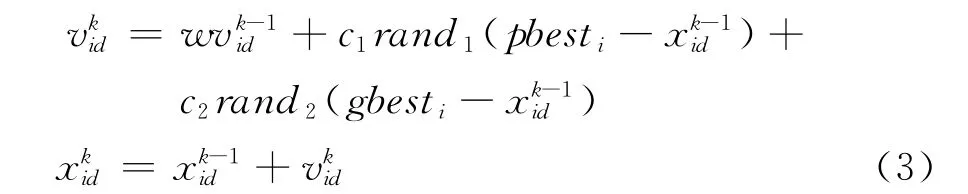
式(3)中i=1,2,...,m;d=1,2,...,n;m為粒子的個數;n是解向量的維數。vi是粒子的速度,xi是粒子的位置。pbest和gbest分別是個體極值和全局極值,c1和c2通常等于2,rand1和rand2是兩個獨立的介于[0,1]之間的隨機數;w是動量項系數,調整其大小可以改變搜索能力的強弱,本文取0.75[8]。
本文以水平軸風力機為研究對象,優化設計編程方框圖如圖4所示。
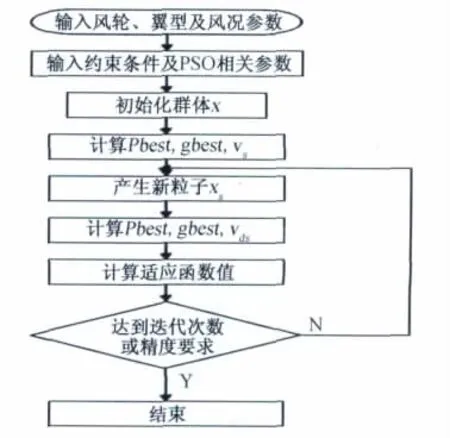
圖4 粒子群算法流程圖Fig.4 Flow chart of PSO program
3 風力機槳距氣動設計的PSO實現
文中采用風力機專用翼型S809,以設計一1.5MW的恒速變槳風力機為例進行優化設計。該風力機的主要氣動與幾何參數為:直徑D=70m,額定風速V0=12m/s,切入風速Vin=3m/s,切出風速Vout=25m/s,額定轉速n=18.8rpm,額定功率W=1500kW,葉片數z=3。葉片幾何外形設計結果如表1所示。
3.1 槳距氣動的優化分析
對于大型恒速變槳風力機組,當風速低于額定風速時,應使風輪的槳距角向負方向調節,來維持最佳攻角,以提高風能利用系數。即V<V0時,以各個風速下需調節的變槳角為搜索變量,目標函數為:f1(Δφ)=CP(Δφ,V),給出變槳角 Δφ的約束范圍:φmin<Δφ<φmax搜索使f1(Δφ)達到最大值時的值,即得到各個風速下調槳距的角度。
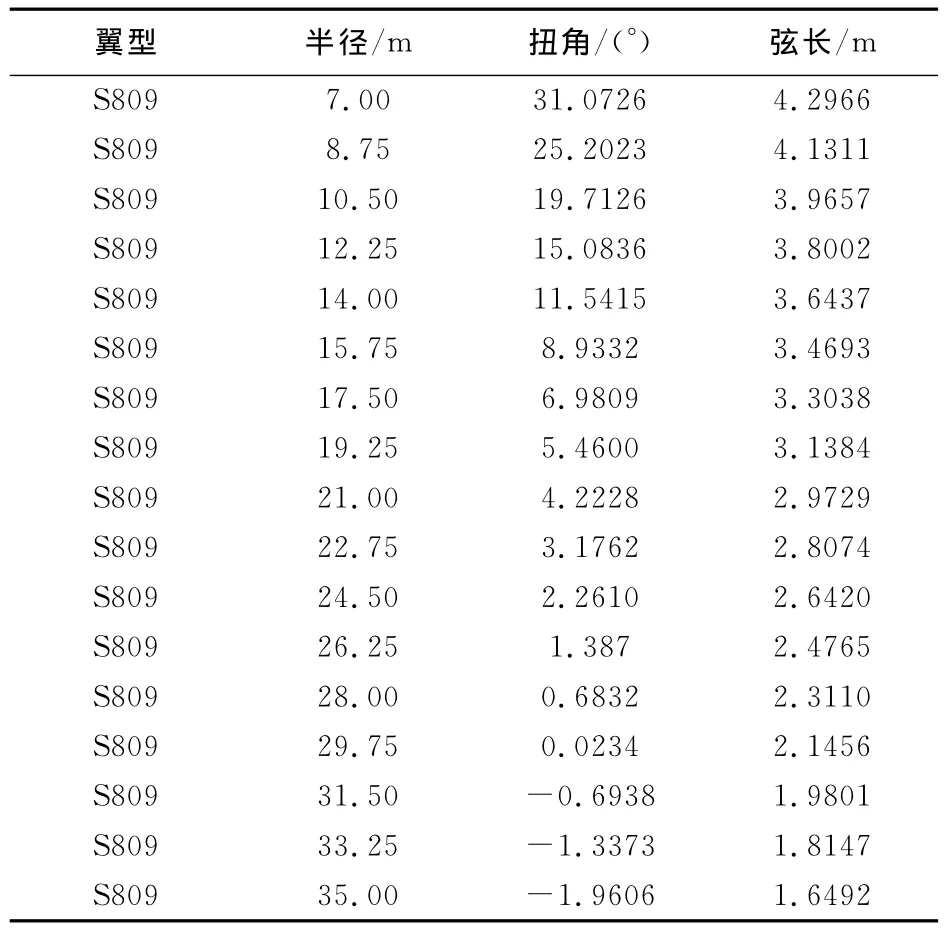
表1 優化設計結果Table 1 The results of optimal design
當風速高于額定風速時,應使風輪的槳距角向正方向調節,攻角變小,減小風能利用系數來保證額定功率的輸出。即V>V0時,求出各欲設計風速下應滿足的各個CP值,使其作為目標向量,各風速下應滿足的變槳角作為搜索變量,目標函數為兩個向量差的模:f2(Δφ)=|CP(Δφ,V)-CP|給出變槳角 Δφ的約束范圍:φmin<Δφ<φmax搜索使f2(Δφ)達到最小值零時的Δφ值,即得到各風速下調槳距的角度。
風輪經槳距調節后,所改變的只是其各徑向位置處的葉片安放角。根據調槳后安放角的更新和原額定的葉片氣動與幾何參數(直徑,弦長,翼型及其氣動性能系數),即可計算風輪在各風速下的氣動性能。
3.2 優化設計結果
根據PSO流程圖,搜索出Δφ,各風速下槳距調節值如圖5所示。優化設計出的槳距調節值變化曲線呈線性分布,易于調節,這和現行槳距角調節理論相吻合。
根據槳距調節公式φ(v)=φ(v0)±Δφ(v),結合額定的葉片氣動與幾何參數,即可計算風輪在各風速下的氣動性能:風能利用系數CP(V),軸向力系數CF(V),出力的轉速特性P(V),及軸向力的轉速特性F(V)。
各風速下槳矩調節設計計算結果及氣動性能曲線分別如表2和圖6-7所示。
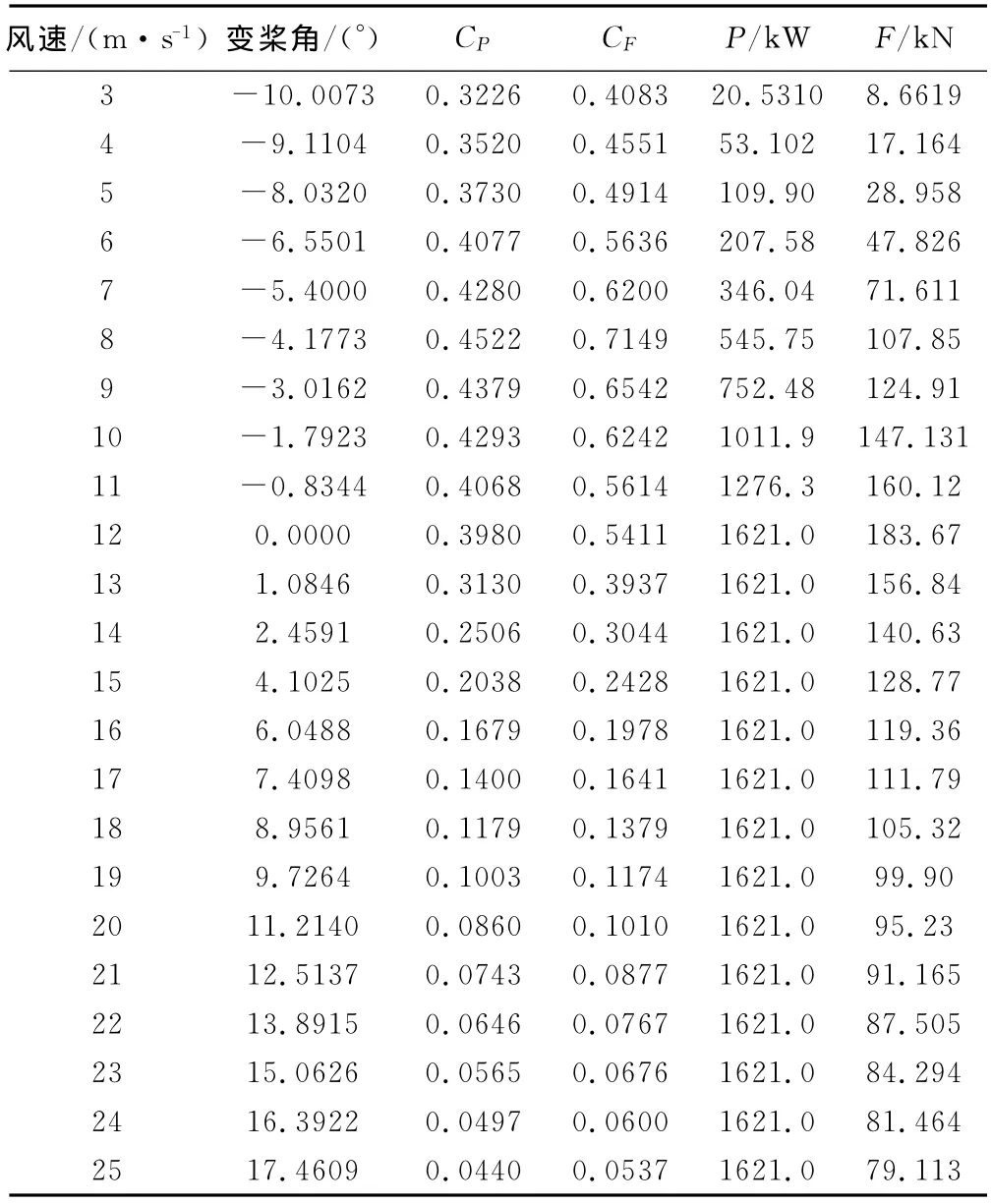
表2 槳矩調節設計計算結果Table 2 The design results of the pitch regulation
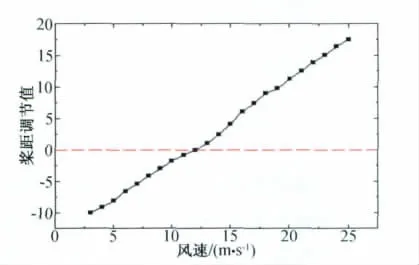
圖5 槳距調節曲線Fig.5 The pitch regulation curve

圖6 功率系數和功率曲線Fig.6 Power coefficient and power curves

圖7 軸向力系數和軸向力曲線Fig.7 The axial force coefficient and axial force curves
3.3 結果分析
(1)從氣動外形優化設計的結果(見表1)可以看出,基于有限葉片變環量的氣動模型與粒子群算法相結合的優化設計計算方法設計出的風力機葉片,其安放角和弦長沿葉片展向分別按貝塞爾曲線和線性進行分布,這與同類型同功率風力機沿葉片展向所設計的安放角和弦長分布情況趨勢一致,說明了本文的優化設計計算方法是可行的。
(2)從槳距氣動優化設計的結果(見圖5)可以看出,當風速小于額定風速12m/s時,槳距角需往負方向調節;當風速大于額定風速12m/s時,槳距角需往正方向調節,這與槳距角調節理論相吻合。
(3)從槳距氣動優化設計的計算結果(見圖6、圖7)可以看出,計算出的CP(V)、CF(V)在風速等于8m/s時達到最大值,隨著風速的逐漸增大其值逐漸減小;功率P和軸向力F從切入風速到額定風速呈上升趨勢,從額定風速到切出風速,由于對槳距進行調節功率P保持不變,軸向力F逐漸減小。這與現行風力機槳距調節的氣動性能曲線變化一致。從而進一步說明本設計計算方法的可行性。
4 結 論
(1)本文采用基于有限葉片變環量的氣動模型,結合粒子群算法對大型風力機槳距調節進行了氣動優化設計和計算,優化設計計算出的特性變化趨勢與實際風力機運行相符,證明了該設計計算方法的可行性和有效性。
(2)為保證設計結果為全局最優解,并加快搜索的速度,文中采用了粒子群算法,這種方法在風力機氣動優化過程中,可以更快收斂于最優解,保證了解的質量。
[1]GOURIERES D L.Wind power plants:theory and design[M].NewYork:Pergamon Press,1982.
[2]賀德馨.風工程與工業空氣動力學[M].北京:國防工業出版社,2006.
[3]葉杭冶.風力風電機組的控制技術[M].北京:機械工業出版社,2002.
[4]CHENG Z X,YE Z Q,CHEN J Y,et al.Aerodynamic optimization for the rotor of horizontal-axis wind machine[A].Proceedings of the International Conference on New and Renewable Energy[C].Beijing,1990.
[5]BURTON T,SHARPE D,JENKINS N,et al.Wind energy handbook[M].Chichester:John Wiley & Sons,Ltd,2001.
[6]SPERA D A,et al.Wind turbine technology:fundamental concepts of wind turbine engineering[M].New York:ASME Press 1994.
[7]KRAMER R,ARCHER R.Modelling approaches for flow over a wind turbine blade[J].WindEngineering,2004,28(3):311-323.
[8]汪定偉,王俊偉,王洪峰.智能優化方法[M].北京:高等教育出版社,2006.

