自由網(wǎng)平差的近似坐標影響研究

周 蘊

(鄭州市規(guī)劃勘測設(shè)計研究院，鄭州450052)

1.引言

經(jīng)典平差中，都是以已知的起算數(shù)據(jù)為基礎(chǔ)，將控制網(wǎng)固定在已知數(shù)據(jù)上。如水準網(wǎng)必須至少已知網(wǎng)中某一點的高程，平面網(wǎng)至少要已知一點的坐標、一條邊的邊長和一條邊的方位角。當(dāng)網(wǎng)中沒有必要的起算數(shù)據(jù)時，我們稱其為自由網(wǎng)，網(wǎng)中沒有起算數(shù)據(jù)時的平差方法，即自由網(wǎng)平差［1，2］。

邊角網(wǎng)中，選取的參數(shù)往往是待定點的坐標，而觀測值一般為方向值、角度值或邊長，因而觀測值和參數(shù)之間建立的關(guān)系均是非線性函數(shù)［3］。如果不給出近似坐標，觀測方程就無法線性化，誤差方程就無法列出。因此如何選取近似坐標，假定自由坐標在自由網(wǎng)平差中的可靠性是個不容忽視的問題。本文對自由網(wǎng)平差中選用不同近似坐標對平差計算結(jié)果的影響進行了詳盡的分析和研究。

2.自由網(wǎng)平差原理

函數(shù)模型:

隨機模型:

其中R(A)=t-d，d為秩虧數(shù)，在最小二乘原則下，求得法方程為:

式中R(N)=R(A)=t-d。由于N是奇異的，即法方程是相容方程，它可以有無數(shù)解。因此，附加一個最小范數(shù)條件:

從而得到法方程的唯一解:

(5)式中，N+為N的偽逆，上述平差方法即為秩虧自由網(wǎng)平差。

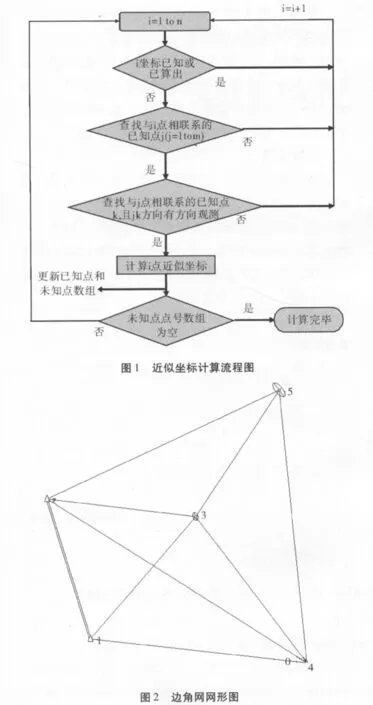
3.近似坐標的計算

考慮到變形監(jiān)測的邊角網(wǎng)大多為邊角同測網(wǎng)，在計算近似坐標時可采用極坐標法。極坐標法的基本思路:若存在已知方位角，首先判斷該方位角的起點是否是已知點A，終點是否是所求的待定點P，如果是，搜索邊長AP即可按極坐標公式計算坐標;若沒有已知方位角或其終點不是P，則搜索與P有方向觀測的已知點A，再由A搜索另一個已知點B，且A到B有方向觀測值，于是可求出AP的方位角，再搜索AP的邊長觀測值，由極坐標公式即可計算P點的坐標。坐標計算的流程圖如圖1所示:

4.不同近似坐標得到的平差結(jié)果比較

為驗證不同近似坐標對平差結(jié)果的影響，本文采用的數(shù)據(jù)為pad2002邊角網(wǎng)算例(原網(wǎng)形如圖2)并選取如下3個參考系:

1)參考系:原點為1號點，1-3方向方位角為0

2)參考系:原點為1號點，1-4方向方位角為0

3)參考系:1 號點(31250.250，11500.410)，2號點(33256.570，10900.840)

對3個參考系，采用上述計算方法計算近似坐標并進行自由網(wǎng)平差，結(jié)果見表1、表2。

4.1 觀測值改正數(shù)分析

表1 邊長平差值改正數(shù)

由表1，2可知，邊長改正值相差最大為0.06 mm，方向改正值相差最大為0.02s。在誤差允許的范圍內(nèi)，可以認為改正數(shù)是相同的。

4.2 三種不同近似坐標參考系迭代次數(shù)

參考系1:5

參考系2:4

參考系3:3

可見采用不同的參考系，需要迭代的次數(shù)是不完全相同的，這和坐標近似值的準確程度有關(guān)。

表2 方向平差值改正數(shù)

4.3 三種不同近似坐標參考系的控制網(wǎng)網(wǎng)圖及誤差橢圓

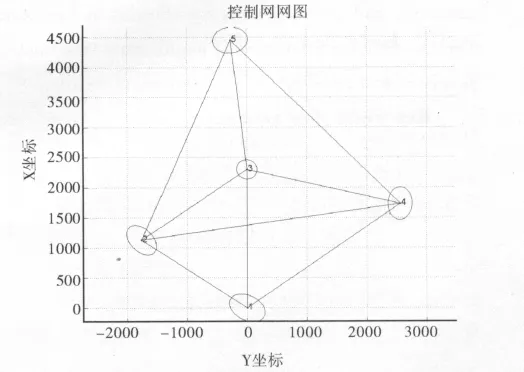
圖3 控制網(wǎng)網(wǎng)圖及誤差橢圓(參考系1)

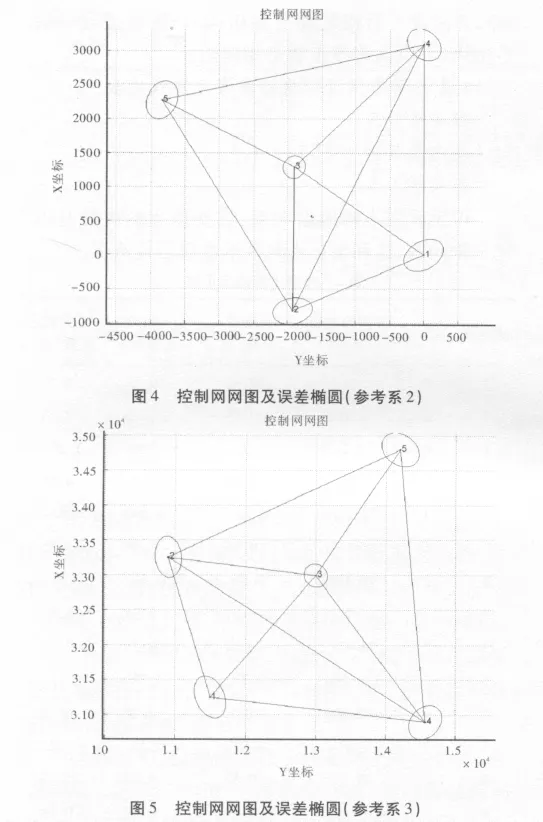
從圖3、圖4、圖5三幅不同近似坐標參考系的控制網(wǎng)網(wǎng)圖及誤差橢圓圖可以明顯看出，不論是控制網(wǎng)的網(wǎng)形，還是誤差橢圓的方向和形狀，都僅僅是旋轉(zhuǎn)。從改正值和誤差橢圓的分析，可以看出控制網(wǎng)選用不同的近似坐標系統(tǒng)進行平差有相同的改正數(shù)和相同的網(wǎng)形及誤差橢圓。

5 結(jié)束語

本文研究了自由網(wǎng)平差中選用不同參考系的近似坐標，因近似坐標的準確度，對平差迭代次數(shù)有一定影響，而平差數(shù)據(jù)的觀測值的平差值，以及平差后的點位坐標并不影響。表明在變形監(jiān)測數(shù)據(jù)的嚴密平差中(迭代次數(shù)足夠)，采用不同的近似坐標對平差結(jié)果的影響幾乎可以忽略。

［1］朱建軍，賀躍光，曾卓喬.變形測量的理論與方法［M］.長沙：中南大學(xué)出版社，2004.

［2］陶本藻.自由網(wǎng)平差與變形分析［M］.武漢：武漢測繪科技大學(xué)出版社，2001.

［3］武漢大學(xué)測繪學(xué)院測量平差學(xué)科組.測量平差基礎(chǔ)［M］.武漢：武漢大學(xué)出版社，2003.