相變材料熱控系統內部接觸熱阻的辨識方法研究

石友安，桂業偉，杜雁霞，曾 磊，錢煒祺

（中國空氣動力研究與發展中心，四川 綿陽 621000）

0 引 言

兩種相互接觸的固體材料的交界面，由于表面粗糙度的存在，微觀上會呈現出“非一致接觸”。當熱流從一種材料經過界面向另一種傳遞時，由于“非一致接觸”的存在，傳熱方式將發生變化：導熱部分的熱流將向接觸點處收縮，空穴內的氣體會帶來對流傳熱，高溫情況下，非接觸的壁面還會發生輻射換熱。這些變化都將對熱量的傳遞形成一種阻礙作用，表現為界面附近的溫度分布明顯的降低，如圖1所示。表征界面因非一致接觸而產生的阻礙熱流傳遞作用的物理量稱為接觸熱阻［1］，數學定義式為：Rc＝ΔT／q。

相變材料熱控系統是航天器及空間飛行器常用的一種熱控系統。在封裝過程中，由于材料凝固時的體積變化將導致相變材料與容器壁面之間形成非一致接觸，從而產生接觸熱阻。對于高溫條件下的熱控系統而言，接觸熱阻的存在，在一定程度上降低了傳熱效率，容易產生局部高溫，引發局部熱應力，甚至帶來局部破壞［2］。接觸熱阻已逐漸成為高溫條件下熱量精確控制的一項瓶頸因素。圖2顯示了在不考慮接觸熱阻情況下，以正二十八烷為相變材料的熱控裝置的計算與實驗吸熱融化過程相界面運動速度的比較。

圖1 微觀視角下的界面傳熱方式Fig.1 Heat transfer in interface between solids in microscopic view

由于接觸界面處傳熱機理復雜、影響因素眾多，譬如接觸壓力、界面溫度等，且相變材料與容器之間的接觸熱阻又與材料凝固過程晶體的形成和生長特性密切相關，現有的理論計算方法大多過于簡化，無法直接應用于工程實際。因此，采用反演熱傳導反問題的方法，將參數辨識中的靈敏度法和共軛梯度法應用到實驗，建立了一種可用于穩態和瞬態接觸熱阻評估的辨識方法。通過模擬辨識和初步應用，得到了一些有意義的結論。

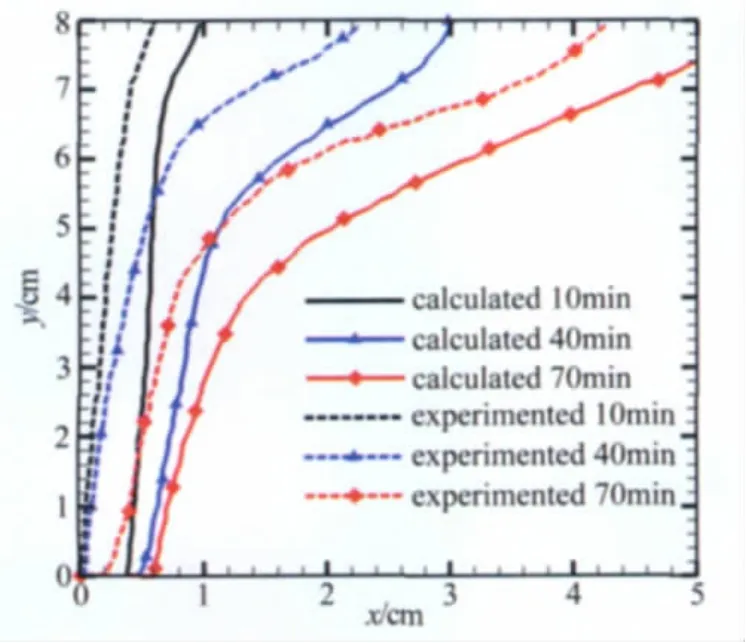
圖2 在不考慮接觸情況下，正二十八烷的計算與實驗相界面移動特性比較Fig.2 Comparison of phase interface of C28H58between computation and experiment without consideration of thermal contact resistance（Rc）

1 計算模型

考慮接觸熱阻時材料融化的計算模型如圖3所示。此時，材料內部的傳熱過程分為熔化前的導熱過程和熔化開始后的固／液相變過程。

將傳熱簡化為一維問題，則控制方程如下：

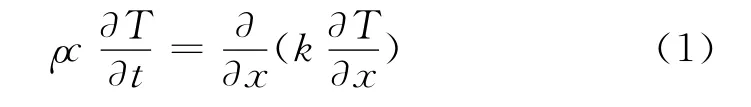
不考慮接觸熱阻時，邊界條件為第一類邊界條件：

初值條件：t＝1，T＝T0；

考慮接觸熱阻時：

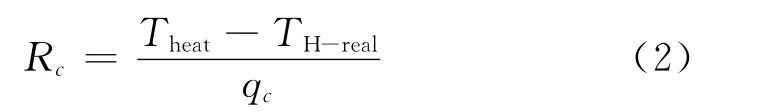
此時，固體內部的傳熱仍然滿足一維傳熱方程，即式（1），但是，邊界條件不同：

初值條件：t＝0，T＝T0；

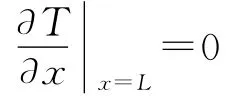
綜上所述，當存在接觸熱阻時，內部傳熱機制不變，但是邊界條件等效為從第一類轉變為第三類。

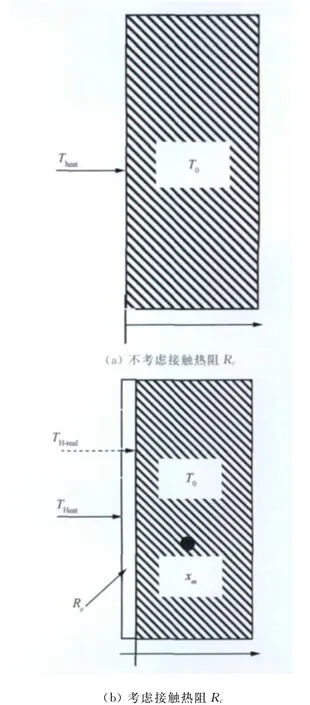
圖3 熱控裝置內接觸熱阻的計算模型Fig.3 Calculation model of Rcin heat control equipment

2 參數辨識方法

辨識求解的思路是：以接觸點測量溫度Tm的時間歷程為依據，在數值求解熱傳導正問題的基礎上，根據輸出誤差原則，將反問題轉化為一個優化問題來處理，等價于在函數空間中尋求合適的函數Rc或Rc（t）或Rc（xm，t），使如下目標泛函達到極小的過程：

式中符號意義：測點的坐標xm；測量溫度Tm；計算溫度T；測量誤差ε。

2.1 穩態接觸熱阻的辨識

采用靈敏度法進行穩態接觸熱阻［3］的辨識，其優化策略是牛頓 拉夫遜（Newton－Raphson）算法［4］。下面介紹算法：

首先根據輸出誤差原則建立目標泛函：

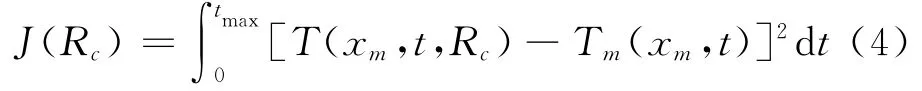
優化算法描述如下：

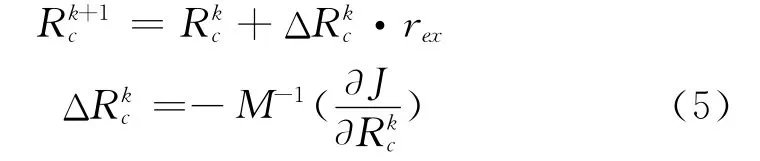
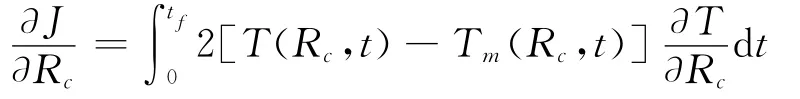
式中，參數的上標k，k＋1分別表示迭代前、后的參數值，rex是松弛因子。式中?T／?Rc為靈敏度，可以通過求解靈敏度方程得出。將式（1）對參數求導后即得到靈敏度方程。具體形式為（U定義為?T／?Rc）：

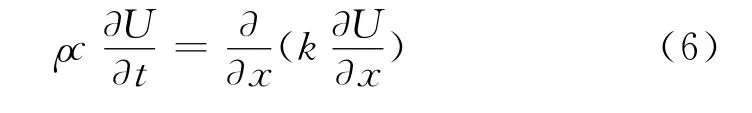
初值條件：t＝0，U＝0；

至此，穩態接觸熱阻辨識基本建立，依據式（5）進行辨識即可得到Rc。

2.2 瞬態接觸熱阻的辨識

相較于穩態而言，瞬態接觸熱阻［5］更能細致地刻畫接觸熱阻的變化關系。采用共軛梯度法［6－7］進行辨識。算法描述：

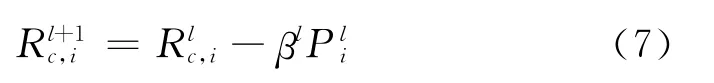
式中下標i表示接觸熱阻的時間離散次數；上標l、l＋1表示迭代層次，β為步長，P為共軛梯度，具體優化過程表述如下：

式中：J′l＝ （?J／?Rc，i）l

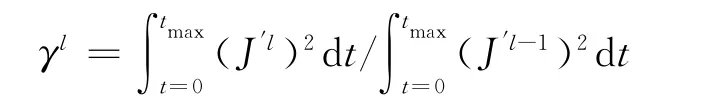
J′l－1和J′l是第l－1步和l步迭代的梯度下降方向，可以采用靈敏度分析或求解伴隨方程來獲取。由于滿足目標泛函的溫度場T，也必須滿足主控方程，因此可根據拉格朗日乘數原理對目標函數進行擴展，得到如下擴展泛函：

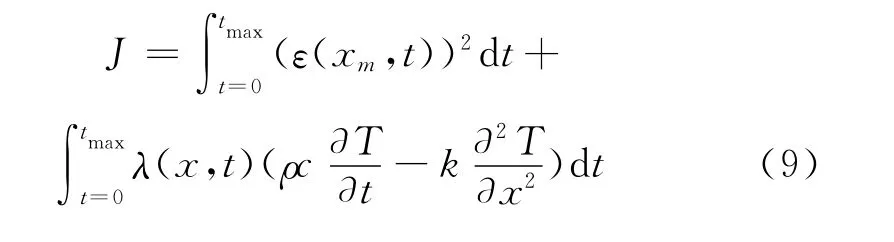
式中λ為伴隨變量。對上式后半部分積分再做變分，得到伴隨方程：

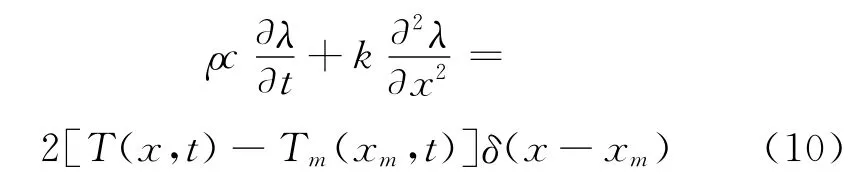
初值條件：t＝tmax，λ（x，tmax）＝0

邊值條件：λ（0，t）｜x＝0＝0；

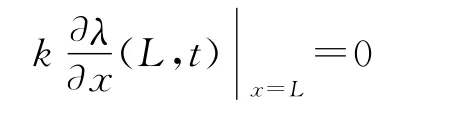
式中δ為克羅內克符號。整理得到，目標函數對Rc（T）的梯度為：

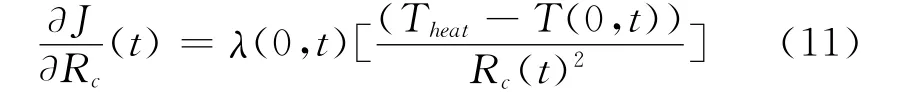
步長由下式計算：

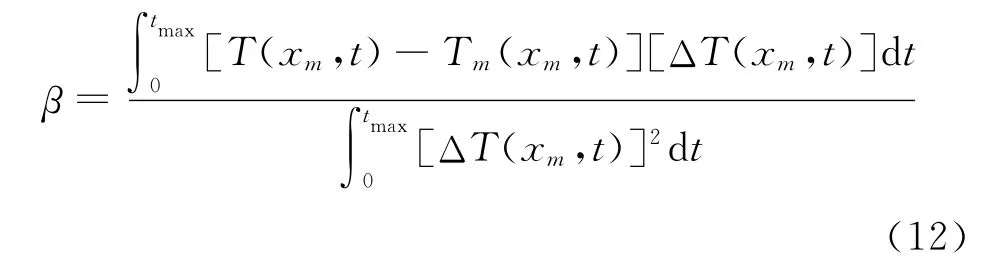
式中ΔT是由ΔR＝λn引起的溫度場的變化值，可通過解靈敏度方程獲得。

在優化過程中，收斂準則根據輸出誤差原則獲得，即：

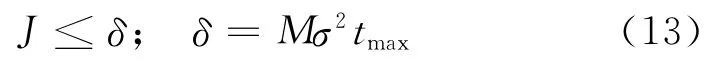
σ為測量誤差的均方差，M為測點數。

至此，共軛梯度法已完全建立，依據式（7）進行辨識即可得到Rc（t）。

3 辨識方法的初步應用

采用封裝二十八烷長方體熱控單元進行融化實驗，實驗系統見圖4，測點位置為x＝0.006m，y＝0.040m。采用電加熱器作為恒溫熱源，溫度控制采用ANV TF100PID自動演算控制器，通過加熱功率的調節實現實驗過程所需的加熱邊界條件，溫度控制精度為±1K。溫度信號由Agilent 34970A多點數據采集器采集。

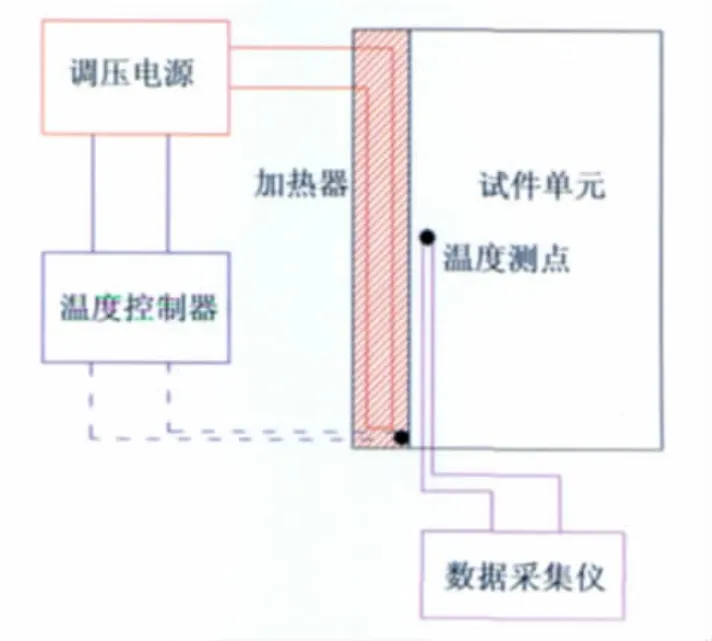
圖4 實驗系統圖Fig.4 Scheme of experiment system

實驗測量溫度數據見圖5，從圖中可以看出，溫升斜率的增長趨勢是先增加后減小，由此可以判定加熱邊界在測量記錄中已經出現了融化。因此，辨識數據選取在0～300s內邊界未融化的一段時間。

圖5 測點溫度數據Fig.5 Data of temperature at measured point

根據測點的溫升歷程測量參數進行辨識。分別取測量時間為100、140s進行穩態接觸熱阻的辨識，得到的結果依次為0.0799和0.0665。圖6是利用穩態辨識值計算得到的測點溫度與實測值的對比。可以發現：采用穩態辨識結果的計算溫度值與實測值存在一定的差異，且隨著時間的增長，差異增大，分析認為隨著相變材料溫度的升高，接觸熱阻可能隨時間發生了變化，穩態接觸熱阻的假設可能帶來了原理性誤差。

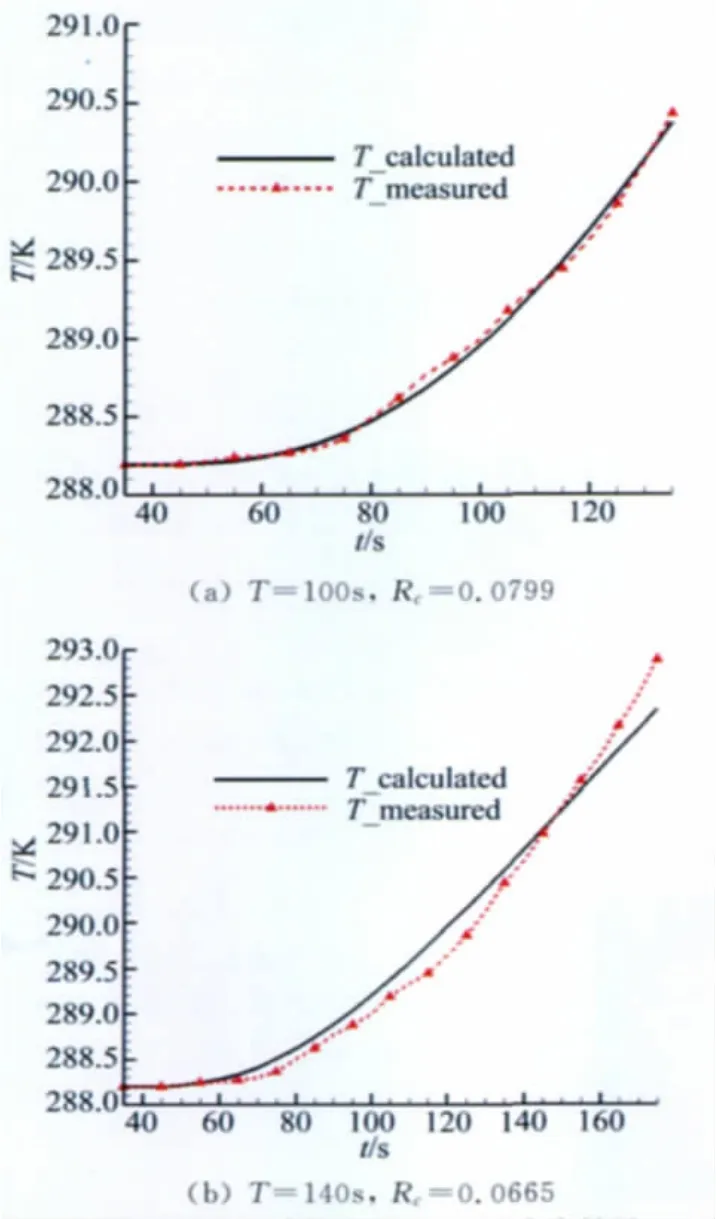
圖6 測量溫度和計算溫度的對比（穩態結果）Fig.6 Comparison of temperature between calculation and experiment in steady Rc

為了提高界面接觸熱阻的辨識精度，進一步開展了瞬態接觸的辨識。圖7是瞬態接觸熱阻的辨識值。圖8是測點的實測溫度和計算溫度的對比。可以發現：利用瞬態辨識值得到的測點計算溫度能夠更好的吻合實測溫度。分析表明，隨著加熱時間的延長，材料溫度不斷升高，壁面和材料之間的空穴對熱流的阻礙作用將減小，當材料出現融化后，融化的液體將填充空穴，接觸熱阻將繼續減小，直至湮滅。這進一步證明了進行瞬態接觸熱阻辨識的可行性和可信性。

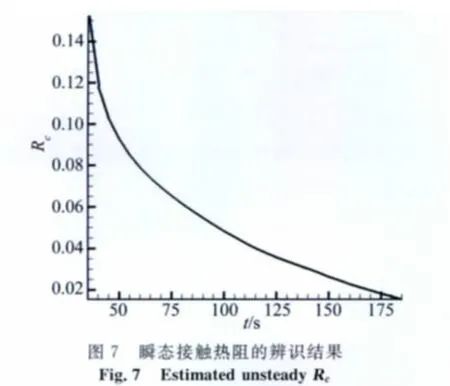
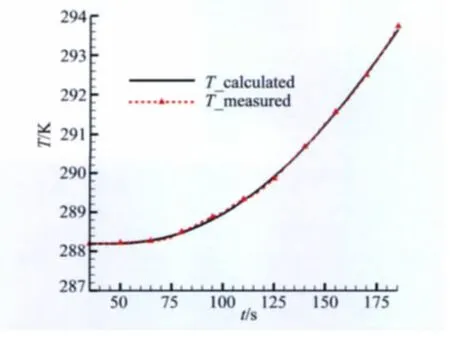
圖8 測量溫度和計算溫度的對比（瞬態接觸熱阻）Fig.8 Comparison of temperature between calculation and experiment in unsteady Re

另外，對影響辨識質量的因素做了初步分析，發現：測溫數據的信噪比是一個影響辨識質量的重要因素。測溫數據是反問題求解的基礎，其信噪比的高低直接決定求解過程能否克服非穩態傳熱固有的擴散性，影響解的穩定性，可參閱文獻［6－8］。保障測量數據具有較高信噪比的措施之一是合理地安排測點的位置。圖8是不同測點處的計算靈敏度的對比。從圖中可以得到：越靠近加熱邊界，靈敏度越高。即在實驗允許的情況下，測點位置宜盡可能地靠近擾動邊界，以獲得較高信噪比的測溫數據。

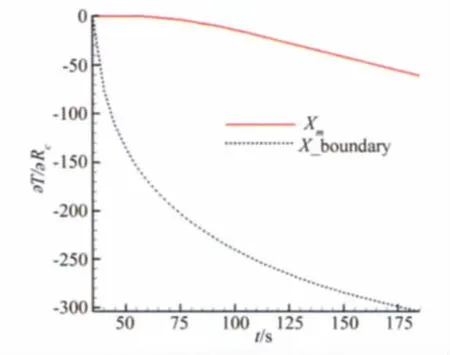
圖9 測點與邊界處的靈敏度的比較Fig.9 Comparison of sensitivity between points in boundary and points in interior

為進一步研究接觸熱阻對材料熔化的延遲作用，初步應用穩態接觸熱阻辨識值，對75℃等溫加熱條件下，考慮和不考慮接觸熱阻效應的材料融化計算速率與相同條件下實驗熔化速率進行了比較，如圖9所示。當計及穩態接觸熱阻時，實驗與計算熔化速率之間的吻合度有所提高，如圖10所示。特別是融化延遲段很好地吻合試驗，說明考慮界面接觸熱阻有利于提高熔化時間的預測準度。

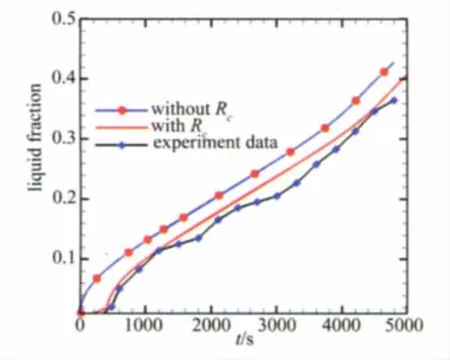
圖10 穩態接觸熱阻對熔化速率的影響Fig.10 Influence of melt rate with consideration of steady Rc

4 小 結

將參數辨識方法引入相變過程界面接觸熱阻的辨識中，將數值計算與實驗相結合，通過參數辨識獲得了界面接觸熱阻的定量參數，對有效評估界面熱阻對相變傳熱的影響作用提供了一種新的思路，得到了一些有意義的結果：

（1）所建立的穩態和瞬態接觸熱阻的兩種辨識算法具有較高的精度、穩定性好、抗噪性強，算法有效；

（2）由于界面熱阻的獲得具有較大難度，采用基于傳熱反問題的參數辨識方法，是獲得相變材料與容器之間界面熱阻的一種有效途徑。該方法對于獲取復合相變材料等不易直接測量的物性參數也具有一定的參考價值；

（3）雖然初步應用驗證了辨識算法的可行性，但是，由于接觸熱阻值較小，影響辨識質量的因素較多，且相變傳熱實驗中還存在一些不確定因素，例如物性隨溫度變化。因此將辨識算法應用于實際工程，還需開展進一步的深入研究。

［1］ MADHUSUDANA C V，FLETCHER L S.Contact heat transfer－the last decade［J］.AIAA Journal，1986，24（3）：510－523.

［2］ WEI D，SUN X S，ZHU J M，et al.Structural response and behavior analysis of steel joint components at elevated temperatures［M］.Key Engineering Materials.2007，353－358：2672－2675.

［3］ JENNIFER Gill，EDUARDO Divo，ALAIN J Kassab.Estimating thermal contact resistance using sensitivity analysis and regularization［J］.Engineering Analysis with Boundary Elements，2009，33：54－62.

［4］ 錢煒祺，蔡金獅.再入航天飛機表面熱流密度辨識［J］.宇航學報，2000，21（4）：1－6.

［5］ FIEBERG C，KNEER R.Determination of thermal contact resistance from transient temperature measurements［J］.International Journal of Heat and Mass Transfer，2008，51：1017－1023.

［6］ 石友安，曾磊，錢煒祺，等.熱參數辨識在測熱試驗中的應用研究［J］.工程熱物理學報，2010，31（9）：1555－1558.

［7］ OLIVEIRAY A P D，ORLANDE H R B.Estimation of the heat flux at the surface of ablating materials by using temperature and surface position measurements［J］.Inverse Problems in Science and Engineering，2004，20（5）：563－577.

［8］ BECK J V，BLACKWELL B，CLAIR C R S.Inverse heat conduction ill－posed problems［M］.New York：John Wiley ＆Sons，1985.