一類具有分布時滯的SIR傳染病模型的穩定性分析
王桂臻,李必文(湖北師范學院 數學與統計學院,湖北 黃石 435002)
0 引 言
數學模型在分析傳染病的傳播和控制方面已經成為重要的工具.近幾十年來,國際上傳染病動力學的研究進展十分迅速,大量的數學模型被用于分析各種各樣的傳染病問題,所涉及的因素也不斷增多,方程的形式越來越復雜,如引起廣泛關注的時滯微分方程模型.時滯在傳染病模型中是廣泛存在的,Betertta等在文獻中研究了一類具有時滯的SIR傳染病模型,他們得到了無病平衡點的全局穩定性和地方病平衡點的局部穩定性;如果時滯充分小,地方病平衡點還是全局穩定的.這是時滯模型的一個基本結果,即地方病平衡點對于小時滯是全局穩定的.2000年,Taketlchi、Ma和Betertta又研究了另一個時滯SIR模型,得到了類似的結果.2002年,Ma和Taketlchi研究了一類具有分布時滯的SIR傳染病模型,得到了只要地方病平衡點存在,模型就是持久的.
在[1]中,已經研究了下面的分布時滯模型
(1)

(2)
滿足初始條件S(0)≥0,I(0)≥0,R(0)≥0.
1 平衡點分析
令系統(2)的右端為零, 可給出系統(2)的平衡點:
2 全局漸近穩定性
由于系統(2)的前兩個方程不依賴于變量R,因此我們僅考慮前兩個方程的穩定性.
定理1 若R0>1 ,那么E*是全局漸近穩定的.

b=βm(S*)I*+μ1S*
(3)
(μ2+λ)I*=βm(S*)I*
(4)

(5)

下面我們來研究Lyapunov泛函的表現形式,定義如下
(6)

用(3)替代b,得到


(7)

用(4)代替(μ2+λ)I*,得

(8)
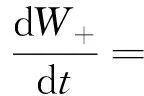

用定積分的分部積分法,我們有
(9)

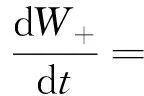

(10)
結合式(7),(8),(10),可得

對上式進行變形,得到


參考文獻:
[1]Takeuchi Y,Ma W,Beretta E.Global asymptotic properties of a delay SIR epidemic model with finite incubation times[J].Nonlinear Anal,2000,42:931~947.
[2]ConnellMcCluskey C.Complete global stability for an SIR epidemic model with delay-Distributed or discrete[J].Nonlinear Analysis:Real World Applications,2010,11:55~59.
[3]Hale J,Lunel S V.Introduction to Functional Differential equations[M].Berlin:Springer-Verlag,1993.
[4]Kar T K,Ashim Batabyal.Stability analysis and optimal control of an SIR epidemic model with vaccination[J].BioSystems,2011,104:127~135.
[5]廖曉昕.穩定性的數學理論及應用[M]. 武漢:華中師范大學出版社,1988.
[6]陳曉英,吳 亭.一類具有分布時滯飽和特性發生率的SIR傳染病模型[J].福州大學學報(自然科學版),2010,38(6):808~812.

