基于飛行品質(zhì)評(píng)估的無(wú)人直升機(jī)魯棒控制器設(shè)計(jì)

劉鵬， 王強(qiáng)， 蒙志君，*， 武哲

1. 北京航空航天大學(xué) 航空科學(xué)與工程學(xué)院， 北京 100191 2. 北京航空航天大學(xué) 自動(dòng)化科學(xué)與電氣工程學(xué)院， 北京 100191

基于飛行品質(zhì)評(píng)估的無(wú)人直升機(jī)魯棒控制器設(shè)計(jì)

劉鵬1， 王強(qiáng)2， 蒙志君1，*， 武哲1

1. 北京航空航天大學(xué) 航空科學(xué)與工程學(xué)院， 北京 100191 2. 北京航空航天大學(xué) 自動(dòng)化科學(xué)與電氣工程學(xué)院， 北京 100191

提出了一種改進(jìn)的無(wú)人直升機(jī)H∞回路成形魯棒控制器設(shè)計(jì)方法。首先將系統(tǒng)辨識(shí)技術(shù)引入到無(wú)人直升機(jī)高帶寬控制器設(shè)計(jì)，根據(jù)飛行掃頻數(shù)據(jù)，得到包含直升機(jī)動(dòng)力學(xué)模型耦合特性的非參數(shù)頻率響應(yīng)，依據(jù)頻率響應(yīng)擬合待辨識(shí)模型得到無(wú)人直升機(jī)高精度的飛行動(dòng)力學(xué)模型。然后根據(jù)該模型，采用改進(jìn)的H∞回路成形方法設(shè)計(jì)了無(wú)人直升機(jī)內(nèi)回路控制器，針對(duì)H∞回路成形方法中權(quán)值矩陣選取困難的問(wèn)題，利用了最大右約數(shù)(GCRD)方法以實(shí)現(xiàn)實(shí)際系統(tǒng)和期望系統(tǒng)的傳遞函數(shù)矩陣之間的轉(zhuǎn)換。與傳統(tǒng)的對(duì)角型權(quán)值矩陣相比，使用此方法成形后的系統(tǒng)具有更寬的魯棒穩(wěn)定裕度，系統(tǒng)的解耦性和頻帶也顯著提高，而且可以大大降低設(shè)計(jì)人員選取權(quán)值矩陣的復(fù)雜性和盲目性。通過(guò)仿真驗(yàn)證，所設(shè)計(jì)的無(wú)人直升機(jī)系統(tǒng)的飛行品質(zhì)滿足軍用標(biāo)準(zhǔn)ADS-33E中一級(jí)區(qū)域的要求。

直升機(jī)； 魯棒控制； 系統(tǒng)辨識(shí)； 最大右約數(shù)；H∞回路成形； 飛行品質(zhì)

近年來(lái)隨著無(wú)人直升機(jī)飛行控制技術(shù)的迅速發(fā)展，無(wú)人直升機(jī)已經(jīng)引起了國(guó)內(nèi)各航空院校、研究院所和軍方的廣泛關(guān)注，但是已有的控制器帶寬較低，而且在風(fēng)干擾等復(fù)雜環(huán)境的控制效果一般[1-3]。究其原因就是缺少高精度的飛行動(dòng)力學(xué)模型阻礙了先進(jìn)的控制算法應(yīng)用于無(wú)人直升機(jī)高帶寬控制器設(shè)計(jì)[4-6]。

頻域辨識(shí)方法是建立高精度的無(wú)人直升機(jī)飛行動(dòng)力學(xué)模型的一種有效方法。直升機(jī)的旋翼、發(fā)動(dòng)機(jī)和傳動(dòng)裝置等高階振動(dòng)將導(dǎo)致飛行試驗(yàn)中測(cè)量噪聲很大，頻域分析可以通過(guò)濾波和相干性分析去除噪聲的影響，而通常采用的時(shí)域辨識(shí)方法由于噪聲對(duì)測(cè)量信號(hào)的影響很大，建立精確的動(dòng)力學(xué)模型比較困難。

H∞回路成形方法是由McFarlane和Glover提出的，它將經(jīng)典控制理論與現(xiàn)代魯棒控制相結(jié)合，是設(shè)計(jì)多輸入多輸出(MIMO)系統(tǒng)魯棒控制器的一種非常有效的方法[7]。盡管設(shè)計(jì)者利用工程經(jīng)驗(yàn)經(jīng)常會(huì)得到較好的回路成形權(quán)值矩陣和控制器，但是在實(shí)際設(shè)計(jì)過(guò)程中，如何選取合適的權(quán)值矩陣W1和W2得到要求的回路性能指標(biāo)是很不明顯的。這是因?yàn)闄?quán)值矩陣中的每個(gè)變量對(duì)回路奇異值的影響往往并不明確，尤其是在設(shè)計(jì)對(duì)象存在嚴(yán)重的耦合或者是需要選取非對(duì)角型的權(quán)值矩陣的時(shí)候，而且權(quán)值矩陣的選取一般都是靠設(shè)計(jì)者反復(fù)的調(diào)整和試湊，非常耗時(shí)且?guī)в泻艽蟮拿つ啃裕胍玫揭粋€(gè)滿足性能指標(biāo)且具有較高魯棒性的控制器比較困難。

本文采用頻域辨識(shí)方法得到了高精度的無(wú)人直升機(jī)飛行動(dòng)力學(xué)模型，并以此模型為基礎(chǔ)，利用H∞回路成形方法來(lái)設(shè)計(jì)滿足無(wú)人直升機(jī)高性能飛行品質(zhì)的魯棒控制器。在權(quán)值矩陣的選取中采用了最大右約數(shù)(Greatest Common Right Divisors， GCRD)方法，與傳統(tǒng)方法相比飛行性能有了較大的提升。通過(guò)仿真結(jié)果的驗(yàn)證，所設(shè)計(jì)的無(wú)人直升機(jī)系統(tǒng)滿足美國(guó)軍用標(biāo)準(zhǔn)ADS-33E[8]中關(guān)于旋翼機(jī)飛行品質(zhì)的要求。

1 小型無(wú)人直升機(jī)飛行動(dòng)力學(xué)模型

在辨識(shí)試驗(yàn)中使用的小型無(wú)人直升機(jī)是由RaPtor50遙控模型直升機(jī)改裝而成的，如圖1所示。該平臺(tái)具有5路主要操縱輸入，包括總距操縱，航向操縱，橫、縱向周期變距操縱和發(fā)動(dòng)機(jī)油門(mén)操縱，其中總距和油門(mén)操縱存在線性耦合關(guān)系。

圖1 試驗(yàn)使用的無(wú)人直升機(jī)Fig.1 Instrumented robotic helicopter

使用的無(wú)人直升機(jī)飛行動(dòng)力學(xué)模型是通過(guò)一種改進(jìn)的頻域系統(tǒng)辨識(shí)方法得到的[9]。該方法根據(jù)飛行掃頻數(shù)據(jù)，得到包含直升機(jī)動(dòng)力學(xué)模型耦合特性的非參數(shù)頻率響應(yīng)，并根據(jù)頻率響應(yīng)對(duì)待辨模型結(jié)構(gòu)進(jìn)行了簡(jiǎn)化。將模式識(shí)別理論應(yīng)用到搜索狀態(tài)空間模型代價(jià)函數(shù)的最小值中，根據(jù)機(jī)理建模結(jié)果擬合頻率響應(yīng)得到線性的六自由度直升機(jī)狀態(tài)空間模型。通過(guò)時(shí)域驗(yàn)證表明辨識(shí)得到的模型精確地反映了該無(wú)人直升機(jī)的動(dòng)力學(xué)特性。

圖2為橫向通道掃頻數(shù)據(jù)，從圖中可以看到，橫向掃頻輸入和橫滾角速度輸出有很高的一致性，這為系統(tǒng)辨識(shí)提供了很好的頻譜特性，可以通過(guò)相干函數(shù)來(lái)判斷一致性，通常相干函數(shù)值的下限為0.6，低于此下限，辨識(shí)結(jié)果會(huì)產(chǎn)生比較大的隨機(jī)誤差；相干函數(shù)值在0.6或者更高時(shí)，辨識(shí)的模型具有較高的精度[10]。圖3為懸停狀態(tài)下辨識(shí)得到的模型和飛行試驗(yàn)數(shù)據(jù)的頻率響應(yīng)比較，由圖3可見(jiàn)兩者擬合得非常好。

圖2 橫向通道掃頻數(shù)據(jù)曲線Fig.2 Lateral sweep data curve

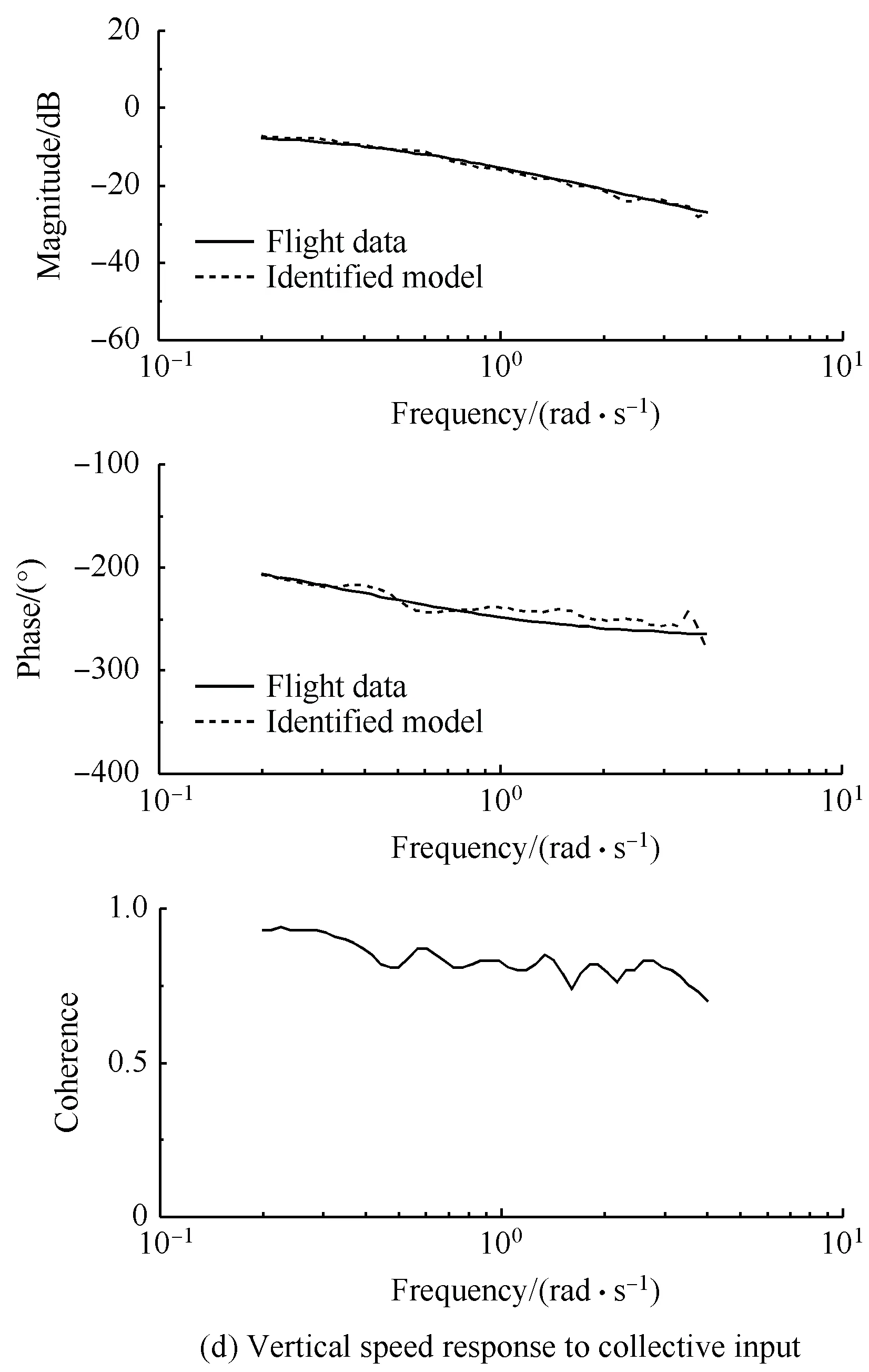
圖3 飛行數(shù)據(jù)和辨識(shí)模型的頻率響應(yīng)比較Fig.3 Comparison between the frequency response from the flight data and the identified model

2 H∞回路成形控制器設(shè)計(jì)

2.1 H∞回路成形設(shè)計(jì)步驟

在得到無(wú)人直升機(jī)高精度的飛行動(dòng)力學(xué)模型后，采用H∞回路成形方法來(lái)設(shè)計(jì)滿足無(wú)人直升機(jī)高性能飛行品質(zhì)的魯棒控制器。H∞回路成形方法的步驟如下[7]：

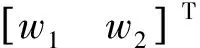
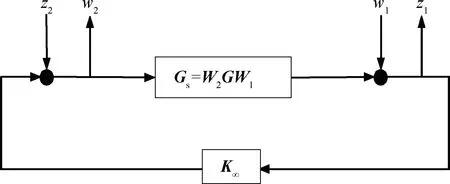
圖4 H∞回路成形結(jié)構(gòu)框圖Fig.4 H∞ loop-shaping standard block diagram

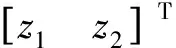
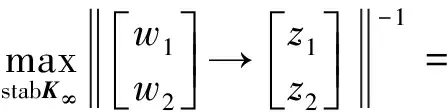
(1)

式中：I為單位矩陣。穩(wěn)定裕度ε的值在0到1之間，它是系統(tǒng)魯棒性和性能的表征。經(jīng)過(guò)理論和實(shí)踐的檢驗(yàn)，當(dāng)ε>0.3時(shí)認(rèn)為系統(tǒng)的性能比較好。H∞回路成形的理論基礎(chǔ)是，如果穩(wěn)定裕度ε的值不是很小，K∞不會(huì)改變期望回路Gs的奇異值。

步驟3檢驗(yàn)閉環(huán)回路的時(shí)域和頻域響應(yīng)以確保系統(tǒng)的飛行品質(zhì)滿足要求，如果不符合則重新調(diào)節(jié)加權(quán)陣并計(jì)算K∞，直到閉環(huán)系統(tǒng)滿足飛行品質(zhì)要求。

2.2 內(nèi)回路設(shè)計(jì)指標(biāo)

由于小直升機(jī)沒(méi)有專門(mén)的飛行品質(zhì)規(guī)范，所以控制器設(shè)計(jì)的最初目標(biāo)是在保證魯棒性的前提下使得系統(tǒng)帶寬盡可能的高。由于H∞回路成形方法比較容易設(shè)定系統(tǒng)帶寬，而且它對(duì)于解決多輸入多輸出系統(tǒng)和對(duì)象不確定性效果很好，因而它用來(lái)解決無(wú)人直升機(jī)控制問(wèn)題非常適合[12]。

圖5 內(nèi)回路控制結(jié)構(gòu)框圖Fig.5 Inner loop block diagram

內(nèi)回路控制器設(shè)計(jì)完成后，應(yīng)用美國(guó)軍用標(biāo)準(zhǔn)中的旋翼機(jī)飛行品質(zhì)規(guī)范ADS-33E來(lái)檢驗(yàn)小直升機(jī)的飛行性能。盡管小直升機(jī)的飛行性能相比大直升機(jī)來(lái)說(shuō)要高一些，然而考慮到加裝了機(jī)載設(shè)備后會(huì)對(duì)小直升機(jī)的飛行性能影響較大，而且舵機(jī)的帶寬也較低，所以通過(guò)設(shè)計(jì)控制器使得小直升機(jī)滿足美軍標(biāo)中關(guān)于大直升機(jī)的飛行品質(zhì)標(biāo)準(zhǔn)，以此來(lái)檢驗(yàn)小直升機(jī)的飛行品質(zhì)是可行的。

在ADS-33E中，對(duì)于內(nèi)回路控制器的飛行品質(zhì)要求如下[8]：

1) 穩(wěn)定性

閉環(huán)系統(tǒng)所有極點(diǎn)都位于s平面左側(cè)，系統(tǒng)單通道的幅值裕度≥6 dB、相角裕度≥45°以保證系統(tǒng)的魯棒性。

2) 帶寬

系統(tǒng)閉環(huán)帶寬應(yīng)滿足ADS-33E等級(jí)1中目標(biāo)對(duì)準(zhǔn)和跟蹤的指標(biāo)要求。對(duì)于θ、φ和r通道，ADS-33E中系統(tǒng)帶寬ωBW的定義是相角為-135°時(shí)的對(duì)應(yīng)的頻率值。θ、φ和r通道的帶寬分別應(yīng)大于2.0，2.5，3.5 rad/s。對(duì)于w通道，ADS-33E中以一階傳遞函數(shù)的形式給出了要求的速度響應(yīng)形式為

(2)

該傳遞函數(shù)用來(lái)擬合w通道的階躍響應(yīng)，擬合后的傳遞函數(shù)要求滿足時(shí)間常數(shù)RTw≤5.0和延時(shí)τw≤0.2，確認(rèn)擬合成功與否的代價(jià)系數(shù)R2的表達(dá)式為

(3)

當(dāng)式(3)的代價(jià)系數(shù)R2在0.97和1.03之間時(shí)，ADS-33E認(rèn)為擬合成功。

3) 解耦

對(duì)于前兩個(gè)傳遞函數(shù)，ADS-33E規(guī)定的階躍響應(yīng)指標(biāo)為

式中：分子Δθpk和Δφpk為本通道作階躍變化時(shí)所引起的其他通道4 s內(nèi)的峰值偏離平衡值的差；分母Δφ4和Δθ4為本通道作階躍變化時(shí)4 s內(nèi)的峰值偏離平衡值的差，它們的比值應(yīng)在規(guī)定的范圍內(nèi)。

對(duì)于第3個(gè)傳遞函數(shù)，ADS-33E等級(jí)1中規(guī)定的w通道的階躍響應(yīng)對(duì)r通道的解耦要求為

式中：r1為3 s前r的峰值，如果沒(méi)有峰值則取r在1 s時(shí)的值r(1)作為r1的值，r3的取值為

r3={

r(3)-r1Whenr1>0

-r(3)+r1Whenr1<0

(4)

4) 擾動(dòng)抑制

各系統(tǒng)的動(dòng)特性響應(yīng)指標(biāo)滿足ADS-33E規(guī)范，即在w、r、φ和θ各通道輸入端加一脈沖擾動(dòng)，系統(tǒng)響應(yīng)應(yīng)在10 s內(nèi)回到峰值的10%范圍內(nèi)。

2.3 權(quán)值矩陣選取的傳統(tǒng)方法

按照2.1節(jié)回路成形步驟設(shè)計(jì)控制器時(shí)，其中最關(guān)鍵但也是最困難的地方就是步驟1中權(quán)值矩陣的選取，如何通過(guò)選取合適的W1和W2來(lái)使得成形后的系統(tǒng)滿足設(shè)計(jì)要求，這一過(guò)程并不明顯，目前為止尚未有系統(tǒng)的設(shè)計(jì)方法，大部分情況下依賴于設(shè)計(jì)人員對(duì)回路成形概念的理解和掌握以及在工程上的經(jīng)驗(yàn)的積累[13]。

一般情況下，W1和W2都選為對(duì)角型矩陣。其中：W1中含有比例積分(PI)環(huán)節(jié)，積分環(huán)節(jié)用來(lái)提高低頻增益，以提高系統(tǒng)的跟蹤性和對(duì)干擾的抑制能力，比例環(huán)節(jié)用來(lái)降低系統(tǒng)由于積分環(huán)節(jié)引起的在穿越頻域附近的相角延遲；W2中含有低通濾波器來(lái)抑制系統(tǒng)高頻段的噪聲。通過(guò)W1和W2確保成形后的系統(tǒng)滿足設(shè)計(jì)要求。

在保證系統(tǒng)魯棒性的前提下，期望成形后的開(kāi)環(huán)系統(tǒng)各通道的穿越頻率不小于7 rad/s，以保證成形后的系統(tǒng)具有較高的帶寬。基于對(duì)回路成形概念的理解和掌握以及在工程上的經(jīng)驗(yàn)的積累，反復(fù)調(diào)整后最終所確定的W1和W2的表達(dá)式為

(5)

(6)

圖6為回路成形前后系統(tǒng)的奇異值曲線，由圖可以看出，成形后的系統(tǒng)的奇異值曲線滿足低頻高增益的要求，而且開(kāi)環(huán)系統(tǒng)各通道的穿越頻率基本滿足設(shè)計(jì)要求。

圖6 G和W2GW1的奇異值曲線Fig.6 Singular value curves of G and W2GW1

在完成了回路成形設(shè)計(jì)后，求解不等式(1)得到24階的狀態(tài)空間形式的K∞控制器，得到的穩(wěn)定裕度ε=0.395。圖7給出了解耦后系統(tǒng)w、r、φ和θ通道包含幅值裕度GM和相角裕度PM的單通道Bode圖。由圖可見(jiàn)，各通道都滿足內(nèi)環(huán)控制器中對(duì)于系統(tǒng)穩(wěn)定裕度的指標(biāo)要求。

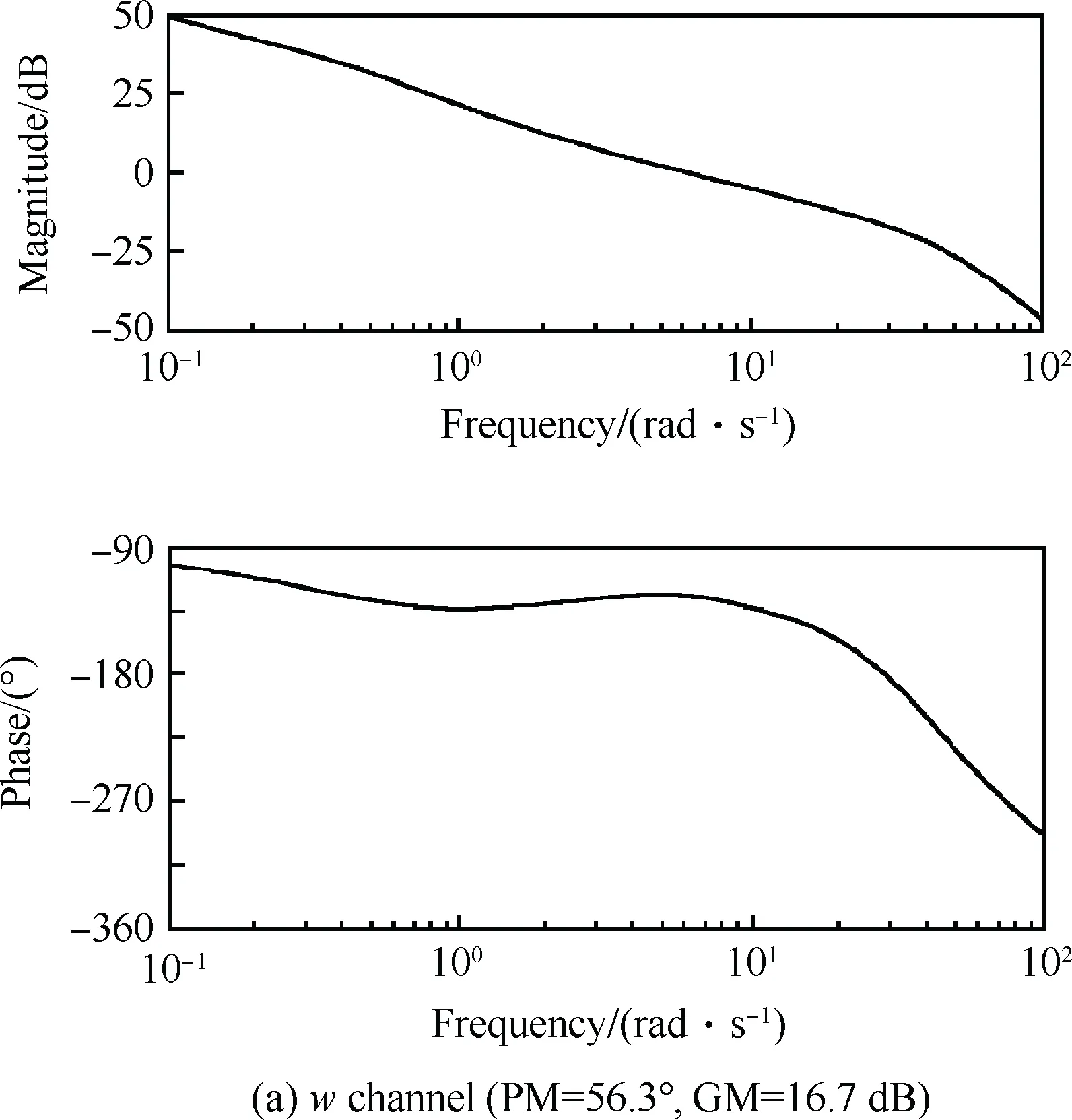
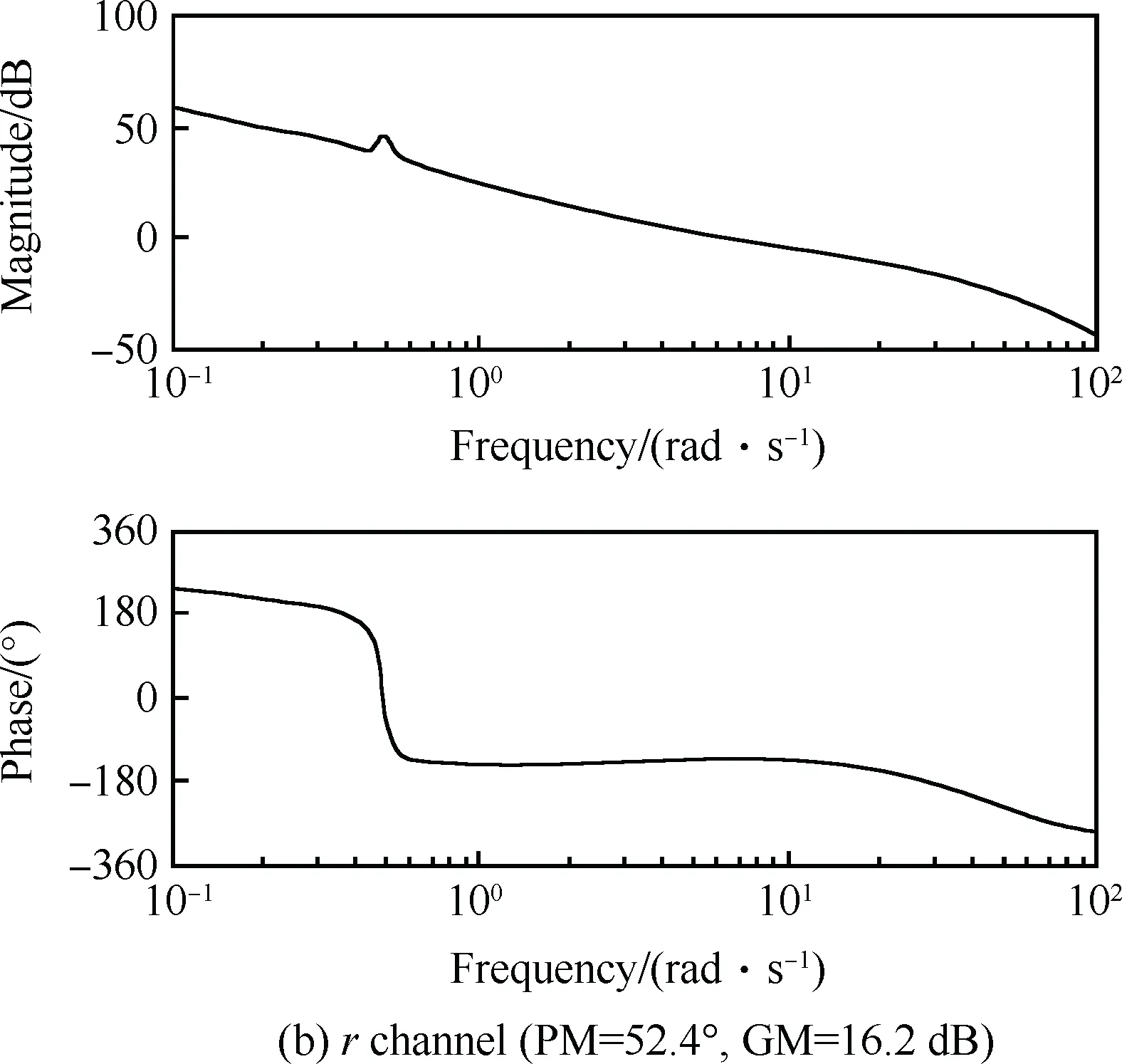
圖7 解耦后系統(tǒng)的Bode圖(傳統(tǒng)方法)Fig.7 Bode plots for decoupling system (traditional method)

2.4 權(quán)值矩陣選取的GCRD方法

對(duì)于一般的系統(tǒng)而言，通過(guò)選取合適的對(duì)角形的權(quán)值矩陣W1和W2是可以使得成形后的系統(tǒng)滿足系統(tǒng)設(shè)計(jì)指標(biāo)的。然而，實(shí)際的設(shè)計(jì)經(jīng)驗(yàn)表明，當(dāng)使用H∞回路成形方法的對(duì)象為通道間耦合性很強(qiáng)的復(fù)雜系統(tǒng)(如直升機(jī)等)，使用對(duì)角型的權(quán)值矩陣進(jìn)行回路成形設(shè)計(jì)時(shí)不能很好滿足期望的設(shè)計(jì)指標(biāo)(通過(guò)2.5節(jié)的仿真結(jié)果比較可以看出)。這時(shí)，就需要設(shè)計(jì)非對(duì)角型的權(quán)值矩陣來(lái)滿足系統(tǒng)期望的設(shè)計(jì)指標(biāo)[14]。

本文利用GCRD方法來(lái)實(shí)現(xiàn)H∞回路成形中實(shí)際系統(tǒng)G和期望系統(tǒng)Gs的傳遞函數(shù)矩陣之間的轉(zhuǎn)換：Gs=GW，該方法的相關(guān)理論參見(jiàn)文獻(xiàn)[15]。

下面將利用GCRD方法來(lái)實(shí)現(xiàn)實(shí)際系統(tǒng)G和期望系統(tǒng)Gs的傳遞函數(shù)矩陣之間的轉(zhuǎn)換。

第1步需要確定期望系統(tǒng)Gs的表達(dá)式，根據(jù)期望成形后的開(kāi)環(huán)系統(tǒng)各通道的穿越頻率不小于7 rad/s的要求，最終確定期望成形的系統(tǒng)Gs為

第2步利用GCRD方法求得H∞回路成形中的實(shí)際系統(tǒng)G和期望系統(tǒng)Gs的傳遞函數(shù)矩陣之間的轉(zhuǎn)換矩陣W，求得W為13階的傳遞函數(shù)矩陣。圖8為實(shí)際成形后的系統(tǒng)L2與期望系統(tǒng)Gs的奇異值曲線比較圖，可以看出，實(shí)際成形后的系統(tǒng)L2與期望系統(tǒng)Gs的奇異值曲線吻合得非常好。

圖8 L2與Gs的奇異值曲線Fig.8 Singular value curves of the real system L2 and the target system Gs

第3步在完成了回路成形設(shè)計(jì)后，求解不等式(1)得到26階的狀態(tài)空間形式的K∞控制器，得到的穩(wěn)定裕度ε=0.696。

通過(guò)上述設(shè)計(jì)步驟可以看出，使用GCRD方法在確定了期望系統(tǒng)Gs的表達(dá)式之后，可以方便地得到權(quán)值矩陣W，不必像傳統(tǒng)方法中去反復(fù)調(diào)節(jié)W1和W2的值以得到滿足指標(biāo)要求的權(quán)值矩陣，而且由于系統(tǒng)耦合較嚴(yán)重，調(diào)節(jié)權(quán)值矩陣中的某個(gè)變量會(huì)對(duì)其他通道的奇異值產(chǎn)生影響，如此反復(fù)的調(diào)整和試湊，非常耗時(shí)且?guī)в泻艽蟮拿つ啃裕胍玫揭粋€(gè)滿足性能指標(biāo)且具有較高魯棒性的控制器比較困難。

而且使用GCRD方法得到的控制器階數(shù)(26階)和使用傳統(tǒng)方法(24階)的差不多，但是穩(wěn)定裕度(ε=0.696)卻比傳統(tǒng)方法的(ε=0.395)提高了將近一倍，可見(jiàn)該方法的有效性。

圖9為解耦后系統(tǒng)包含幅值裕度和相角裕度的單通道Bode圖，可以看出各通道的穩(wěn)定裕度比利用傳統(tǒng)的W1和W2對(duì)角陣成形后的系統(tǒng)更大，且遠(yuǎn)滿足內(nèi)環(huán)控制器中對(duì)于系統(tǒng)穩(wěn)定裕度的指標(biāo)要求。

圖9 解耦后系統(tǒng)的Bode圖(GCRD方法)Fig.9 Bode plots for decoupling system(GCRD method)

2.5 飛行品質(zhì)驗(yàn)證

2.4節(jié)利用權(quán)值矩陣選取的GCRD方法重新進(jìn)行了H∞回路成形設(shè)計(jì)，并比較了使用GCRD方法和使用W1和W2成形(傳統(tǒng)方法)后系統(tǒng)的穩(wěn)定裕度，發(fā)現(xiàn)使用GCRD方法進(jìn)行回路成形后系統(tǒng)的穩(wěn)定裕度明顯提高。下面將針對(duì)ADS-33E中對(duì)于內(nèi)回路控制器的飛行品質(zhì)的其他要求進(jìn)行對(duì)比驗(yàn)證。

1) 帶寬驗(yàn)證

表1為考慮了執(zhí)行機(jī)構(gòu)和傳感器特性的前提下，回路成形后內(nèi)環(huán)的系統(tǒng)帶寬與ADS-33E所規(guī)定的指標(biāo)的對(duì)比。表2為w通道的響應(yīng)速度校驗(yàn)結(jié)果。

表1 校驗(yàn)系統(tǒng)的帶寬Table 1 Bandwidth evaluations for system

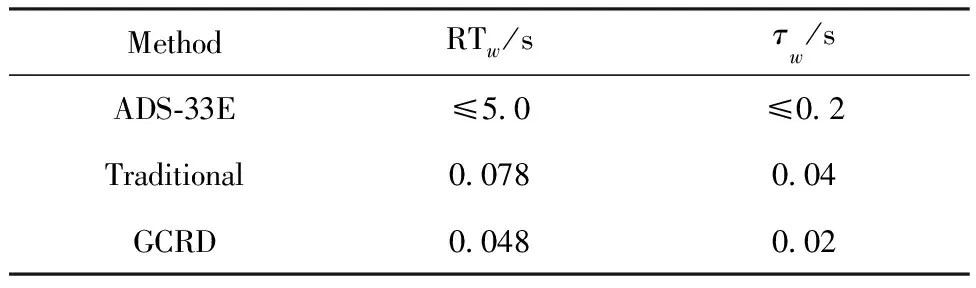
表2 校驗(yàn)系統(tǒng)的響應(yīng)速度Table 2 Response speed evaluations for system

2) 解耦性驗(yàn)證

圖10和圖11分別為使用傳統(tǒng)方法和使用GCRD方法成形后的系統(tǒng)的θ、φ和w通道分別加入5°、5°和1 m/s階躍輸入后的響應(yīng)曲線。根據(jù)階躍響應(yīng)數(shù)據(jù)計(jì)算飛行品質(zhì)中關(guān)于通道間耦合特性的指標(biāo)，表3為回路成形后的系統(tǒng)的耦合性與ADS-33E所規(guī)定的指標(biāo)的對(duì)比，由圖10、圖11和表3可看出，使用GCRD方法比用傳統(tǒng)方法成

圖10 系統(tǒng)耦合性的階躍響應(yīng)驗(yàn)證(傳統(tǒng)方法)Fig.10 Step responses for inter-axis coupling evaluation(traditional method)

圖11 系統(tǒng)耦合性的階躍響應(yīng)驗(yàn)證(GCRD方法)Fig.11 Step responses for inter-axis coupling evaluation (GCRD method)

表3 校驗(yàn)通道間的解耦Table 3 Inter-axis coupling evaluation

3) 擾動(dòng)抑制驗(yàn)證

圖12和圖13分別為在使用傳統(tǒng)方法和使用GCRD方法成形后的系統(tǒng)的θ、φ、w和r通道分別加入幅值為1、寬度為1 s的脈沖擾動(dòng)輸入后的響應(yīng)曲線。由圖可以明顯看出，使用兩種方法后的各通道的響應(yīng)在10 s內(nèi)都已經(jīng)回到峰值的10%范圍內(nèi)，而且使用GCRD方法后的系統(tǒng)對(duì)擾動(dòng)的恢復(fù)的時(shí)間比傳統(tǒng)方法的更短，且振蕩很小，說(shuō)明使用GCRD方法后的系統(tǒng)對(duì)擾動(dòng)的抑制更強(qiáng)。

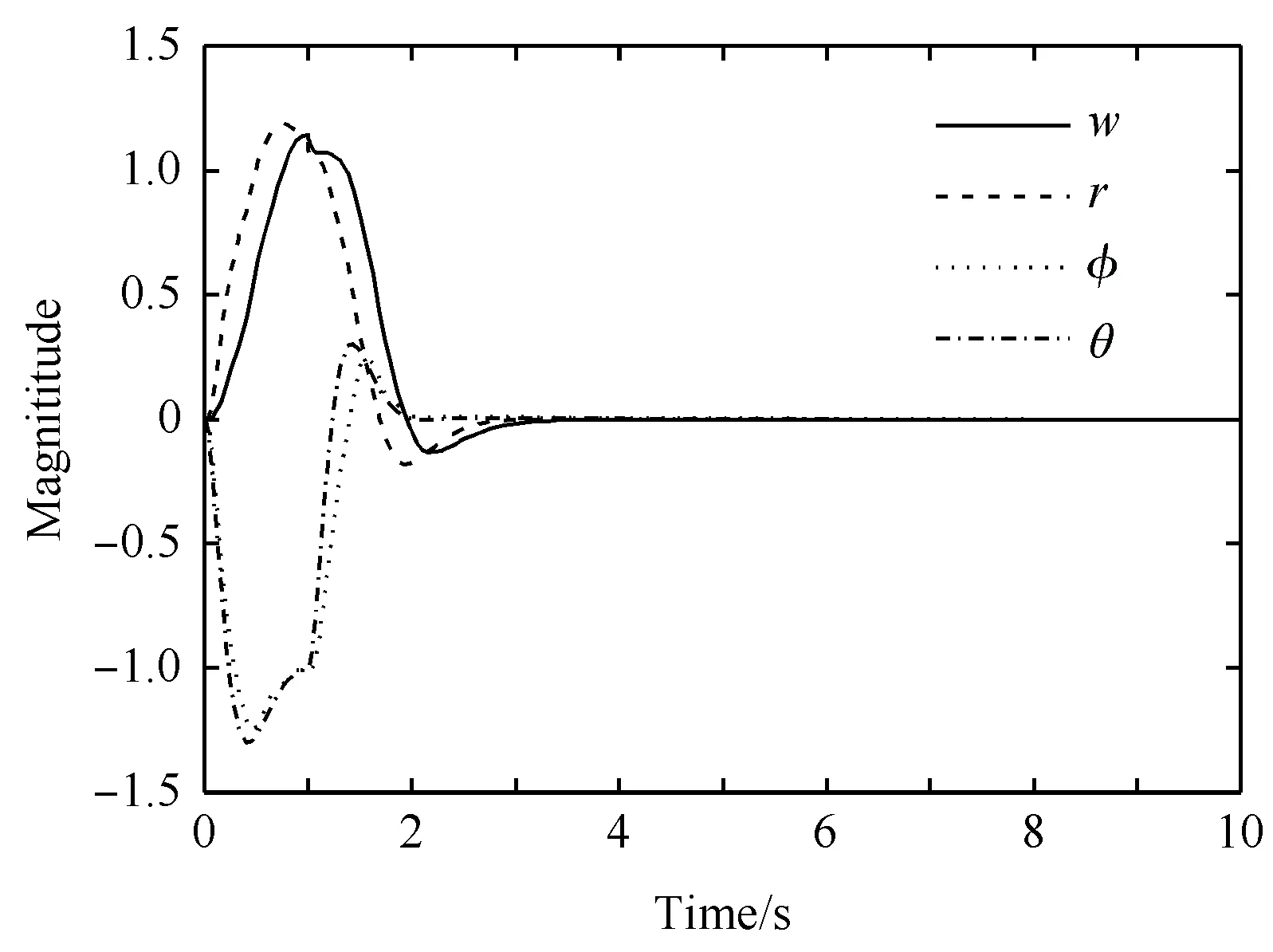
圖12 系統(tǒng)脈沖擾動(dòng)響應(yīng)(傳統(tǒng)方法)Fig.12 Normalized responses to pulse disturbance (traditional method)

圖13 系統(tǒng)脈沖擾動(dòng)響應(yīng)(GCRD方法)Fig.13 Normalized responses to pulse disturbance (GCRD method)

綜上仿真比較可以看出，使用GCRD方法進(jìn)行H∞回路成形后的系統(tǒng)比使用傳統(tǒng)方法的前置和后置的對(duì)角型權(quán)值矩陣W1和W2成形后的系統(tǒng)的飛行品質(zhì)更高，更能滿足ADS-33E中對(duì)于內(nèi)回路控制器的飛行品質(zhì)的要求。

3 結(jié) 論

本文采用了頻域辨識(shí)建模和H∞回路成形方法來(lái)設(shè)計(jì)無(wú)人直升機(jī)高帶寬魯棒控制器，其中重點(diǎn)研究了以下幾個(gè)問(wèn)題:

1) 根據(jù)飛行試驗(yàn)數(shù)據(jù)，采用頻域系統(tǒng)辨識(shí)的方法得到無(wú)人直升機(jī)精確的動(dòng)力學(xué)模型，以此模型為基礎(chǔ)設(shè)計(jì)了高帶寬魯棒控制器。

2) 采用H∞回路成形方法設(shè)計(jì)無(wú)人直升機(jī)內(nèi)環(huán)控制器，實(shí)現(xiàn)系統(tǒng)的解耦和姿態(tài)穩(wěn)定，并保證控制系統(tǒng)具有高帶寬。

3) 通過(guò)仿真驗(yàn)證，GCRD方法是解決H∞回路成形中權(quán)值矩陣選取的一種有效方法，使用此方法設(shè)計(jì)后的系統(tǒng)滿足ADS-33E中關(guān)于一級(jí)飛行品質(zhì)的所有要求。

[1] Kim H J, Shim D H, Sastry S. Flying robots: modeling, control and decision making. Proceedings of the 2002 IEEE International Conference on Robotics and Automation, 2002: 66-71.

[2] Roberts J M, Corke P, Buskey G. Low-cost flight control system for a small autonomous helicopter. Proceedings of the 2002 Australasia Conference on Robotics and Automation, 2002: 546-551.

[3] Shim D H, Kim H J, Sastry S. Decentralized nonlinear model predictive control of multiple flying robots. Proceedings of the 42nd IEEE Conference on Decision and Control, 2003: 3621-3626.

[4] Isidori A, Marconi L, Serrani A. Robust nonlinear motion control of a helicopter. IEEE Transactions on Automatic Control, 2003, 48(3): 413-426.

[5] Ekblad M．Reduced-order modeling and controller design for a high performance helicopter．Journal of Guidance, Control and Dynamics, 1990, 13(3)：439-449．

[6] Enns R, Si J. Helicopter trimming and tracking control using direct neural dynamic programming. IEEE Transactions on Neural Networks, 2003, 14(4): 929-939.

[7] McFarlane D C, Glover K. A loop shaping design procedure using synthesis. IEEE Transactions on Automatic Control, 1992,37(6): 759-769.

[8] Baskett B J. ADS-33E, Aeronautical design standard performance specification handling qualities requirements for military rotorcraft. Alabama： United States Army Aviation and Missile Command, 2000.

[9] Liu P, Wu Z. Modified frequency identification method and its application in helicopter modeling. Control Theory & Application, 2011, 28(12): 1747-1753.(in Chinese)

劉鵬, 武哲.改進(jìn)的頻域辨識(shí)方法及其在無(wú)人直升機(jī)建模中的應(yīng)用. 控制理論與應(yīng)用, 2011, 28(12): 1747-1753.

[10] Tischler M B, Remple R K. Aircraft and rotorcraft system identification: engineering methods with flight test examples. Virginia: American Institute of Aeronautics and Astronautics Press, 2006: 25-53.

[11] Miller R H. A method for improving the inherent stability and control characteristics of helicopters. Journal of Aeronautical Sciences, 1950,17(6): 363-374.

[12] La Civita M, Papageorgiou G, Messner W. Design and flight testing of a high-bandwidthH∞loop shaping controller for a robotic helicopter. AIAA-2002-4836, 2002.

[13] Li W J. Robust control based on loop shaping. Harbin: Department of Control Science & Engineering, Harbin Institute of Technology, 2006. (in Chinese)

李衛(wèi)江. 基于回路成形的魯棒控制研究. 哈爾濱： 哈爾濱工業(yè)大學(xué)控制科學(xué)與工程系, 2006.

[14] Lanzon A. Weight optimization inH∞loop-shaping. Automatic, 2005, 41: 1201-1208.

[15] Le V X, Safonov M G. Rational matrix GCD’s and the design of squaring-down compensators—a state space theory. IEEE Transactions on Automatic Control, 1992,36(3): 384-392.

UnmannedHelicopterRobustControllerDesignBasedonAircraftFlyingQualitiesEvaluation

LIUPeng1,WANGQiang2,MENGZhijun1, *,WUZhe1

1.SchoolofAeronauticScienceandEngineering,BeihangUniversity,Beijing100191,China2.SchoolofAutomationScienceandElectricalEngineering,BeihangUniversity,Beijing100191,China

Arobustautomaticflightcontrolsystemisdesignedforasmallscaleunmannedhelicopterinthispaper.Wefirstapplysystemidentificationtothedesignofahigh-bandwidthcontrollerforrobotichelicopters.Theoverallconceptistoextractacompletesetofnon-parametricinput-to-outputfrequencyresponsesthatfullycharacterizethecoupledhelicopterdynamics,andthenapplyanonlinearsearchalgorithmforalinearhigh-fidelitysimulationmodelthatmatchesthefrequencyresponsedataset.TheH∞loop-shapingmethodisusedtodesigntheinnerloopoftheunmannedhelicopterbasedontheidentifiedmodel.Thegreatestcommonrightdivisors(GCRD)methodisemployedtomovethetransferfunctionmatrixfromtherealsystemtothetargetsystem,whichisaveryusefulwaytosolvethedifficultiesinchoosingaproperweightingmatrixinH∞loop-shaping.Comparedwiththetraditionalmethod,thesystemusingthenewmethodexhibitsalargerrobuststabilitymargin,andthedecouplingandthebandwidthofthesystemarealsoimprovedconsiderably.Furthermore,itreducesthecomplexityandblindnessforthedesignertofindtheproperweightingmatrix.ThesimulationresultsprovethattheunmannedhelicoptersystemachievesatoplevelcontrolperformancethatconformsrelevantrequirementsinmilitarystandardsADS-33E.

helicopter;robustcontrol;systemidentification;greatestcommonrightdivisors;H∞loop-shaping;aircraftflyingqualities

2011-12-28；Revised2012-03-12；Accepted2012-03-19；Publishedonline2012-05-201359

URL：www.cnki.net/kcms/detail/11.1929.V.20120520.1359.018.html

.Tel.：010-82338797E-mailmengzhijun@buaa.edu.cn

2011-12-28;退修日期2012-03-12;錄用日期2012-03-19; < class="emphasis_bold">網(wǎng)絡(luò)出版時(shí)間

時(shí)間：2012-05-201359

www.cnki.net/kcms/detail/11.1929.V.20120520.1359.018.html

.Tel.：010-82338797E-mailmengzhijun@buaa.edu.cn

LiuP,WangQ,MengZJ,etal.Unmannedhelicopterrobustcontrollerdesignbasedonaircraftflyingqualitiesevaluation.ActaAeronauticaetAstronauticaSinica,2012,33(9):1587-1597. 劉鵬，王強(qiáng)，蒙志君，等．基于飛行品質(zhì)評(píng)估的無(wú)人直升機(jī)魯棒控制器設(shè)計(jì)．航空學(xué)報(bào),2012,33(9):1587-1597.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

1000-6893(2012)09-1587-11

V212.4； TP273

A

劉鵬男，博士研究生。主要研究方向：飛行力學(xué)，系統(tǒng)辨識(shí)，飛行控制。

Tel: 010-82338797

E-mail: lppl2008@163.com

王強(qiáng)男，博士研究生。主要研究方向：飛行控制。

Tel: 010-82338797

E-mail: teddywang_0929@126.com

蒙志君男，博士，講師。主要研究方向：飛行器總體設(shè)計(jì)。

Tel: 010-82338797

E-mail: mengzhijun@buaa.edu.cn

武哲男，博士，教授，博士生導(dǎo)師。主要研究方向：飛行器總體設(shè)計(jì)，飛行器隱身設(shè)計(jì)。

Tel: 010-82338797

E-mail: wuzhe@buaa.edu.cn