含膠層復合材料梁構件性能分析

王東方， 楊嘉陵

北京航空航天大學 航空科學與工程學院， 100191 北京

含膠層復合材料梁構件性能分析

王東方， 楊嘉陵*

北京航空航天大學 航空科學與工程學院， 100191 北京

復合材料剪切模量通常比彈性模量低1個數量級，這就導致復合材料梁結構剪切效應比普通梁結構顯著得多，尤其是梁截面高度較大的情況。作為夾膠玻璃等結構的復合材料支撐框架，復合材料方管梁翼緣通常存在較弱的膠層，此時復合材料梁橫截面包含不同剪切模量的材料層，這就導致梁橫截面在剪切作用下發生復雜的翹曲。剪切翹曲效應對梁結構的性能有著極大的影響，本文在分段線性位移場假設基礎上，推導了對稱面內變形的方管梁結構靜力以及自振周期計算模型，并同經典梁理論計算結果進行對比，分析了梁幾何參數、膠層力學參數等因素對兩個模型計算誤差的影響。計算結果表明，當膠層較弱時，弱層帶來的層間剪切效應對梁的性能有著決定性的影響，此時經典梁理論不再適用。

方管梁； 復合材料； 橫截面翹曲； 膠層； 分段線性

近年來，在航空工程中，復合材料層合板得到了廣泛的應用，許多飛機內部都有相當一部分的復合材料承載框架。當前針對復合材料層合板的研究大多集中在復合材料板殼[1-7]上，而針對復合材料梁構件的研究數量[8-15]相對較少，已有的研究基本上集中在薄壁梁構件以及含分層復合材料梁構件[16-18]上，其理論一般都建立在一階剪切基礎上。關于厚壁梁的研究目前還很少見，Kim和White[19-20]采用Reddy建立的整體三次位移場理論[3]建立了閉合厚壁復合材料梁的計算模型。

復合材料框架構件多為方管式梁，為提高梁構件的承載力，通常在梁的上、下表面附加幾片成型復合材料板，此時方管梁翼緣厚度增加，方管梁可能成為厚壁梁。另外在某些型號飛機座艙復合材料結構中，采用復合材料制作的夾膠玻璃邊框架，翼緣存在多層膠層、多層玻璃以及復合材料板。通常來說，復合材料的剪切模量遠低于面內彈性模量，因此同普通梁構件相比，復合材料梁構件的剪切效應對其性能有著更加顯著的影響。而且對于含膠層復合材料層合梁來說，一般情況下膠層的力學性能遠弱于復合材料。在這種情況下，梁構件橫截面將很難滿足平截面假設，此時采用經典梁理論進行求解將不可避免地帶來一定的誤差。當前復合材料梁的研究基本上是基于整體位移場進行計算的，然而當梁橫斷面上各部分剪切模量相差較大且翼緣承擔剪力不可忽略時，復合材料梁橫斷面在剪力作用下的翹曲很難用簡單的整體位移場進行描述，此時將不得不采用分層位移場[21]進行計算。目前關于有弱層的復合材料梁的研究還很少見，為分析膠層以及剪切效應對復合材料梁構件性能帶來的影響，本文假定沿著梁截面高度位移場為分段線性，推導了含膠層復合材料方管梁構件的靜力計算模型與自振頻率計算模型，并同經典梁理論計算結果相對比，分析了兩個模型之間計算誤差的影響因素。

1 復合材料層合梁靜力計算模型

圖1所示復合材料梁為典型的含弱層層合梁構件，假定圖1所示復合材料層合梁在對稱面內彎曲，通常每一片復合材料層合板由幾十層復合材料鋪成(如圖2所示)，如果計算時細化到每一層都假定為位移分段線性，計算量將很龐大，而且也不太必要。由于單片層合板各層剪切模量相差不大且厚度較薄，因此在計算時位移場可假定如下：

1) 上翼緣附加單片層合板沿著厚度方向位移線性分布。

2) 上翼緣膠層沿著厚度方向位移線性分布。

3) 復合材料方管上翼緣位移沿著厚度方向線性分布。

4) 復合材料腹板因截面高度大，剪應力相對較高，為減小誤差，沿著截面高度分為4段，每一段位移沿著截面高度方向線性分布。

5) 下翼緣各層位移場假定同上翼緣。

6) 如果翼緣有多個弱膠層，則應在每個弱膠層界面進行分段，假設整個梁斷面共劃分為m段，則加上上下表面共有m+1個界面。

7) 假設層合梁在對稱面內變形，不考慮z向位移。

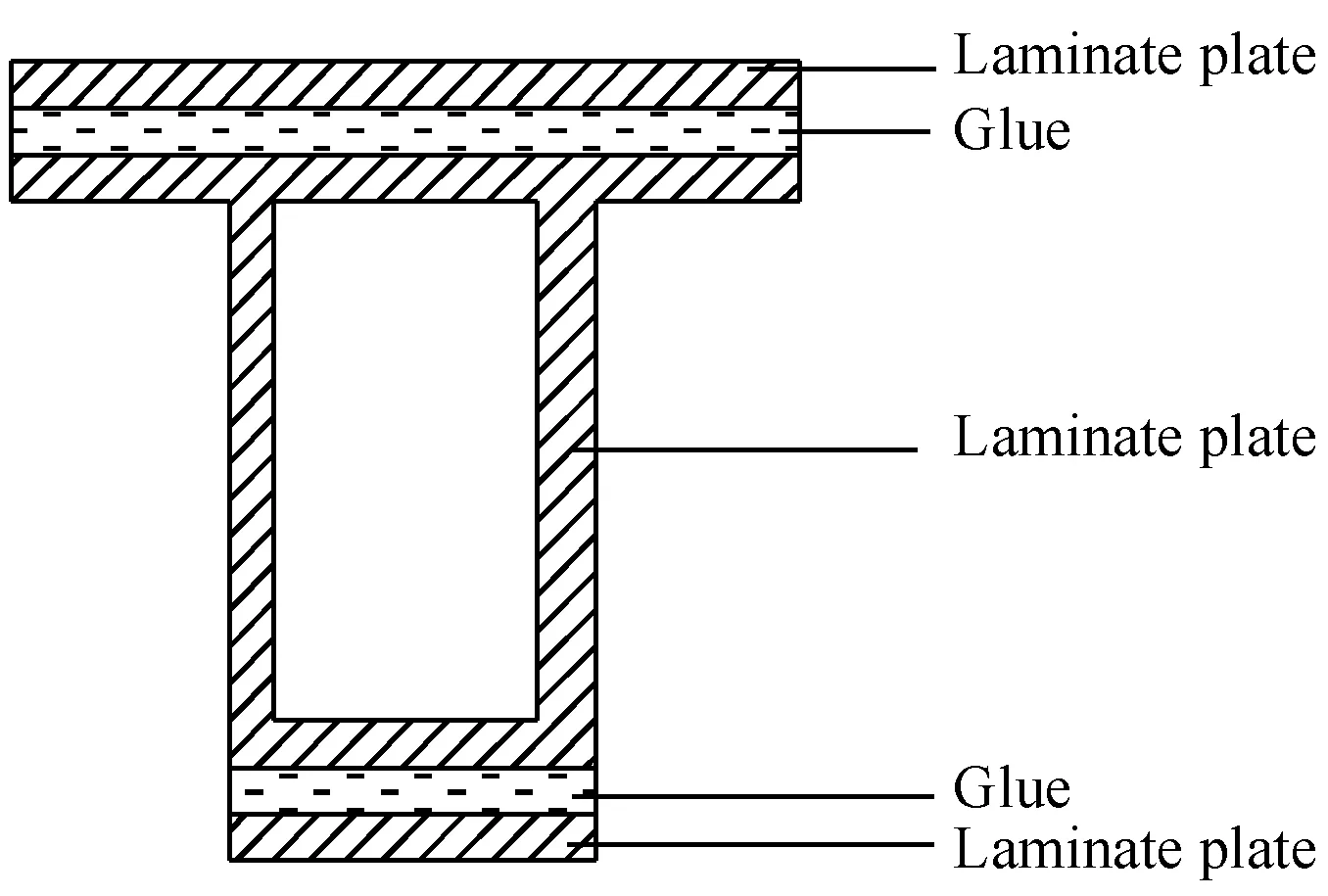
圖1 層合梁橫截面Fig.1 Cross section of a laminate beam

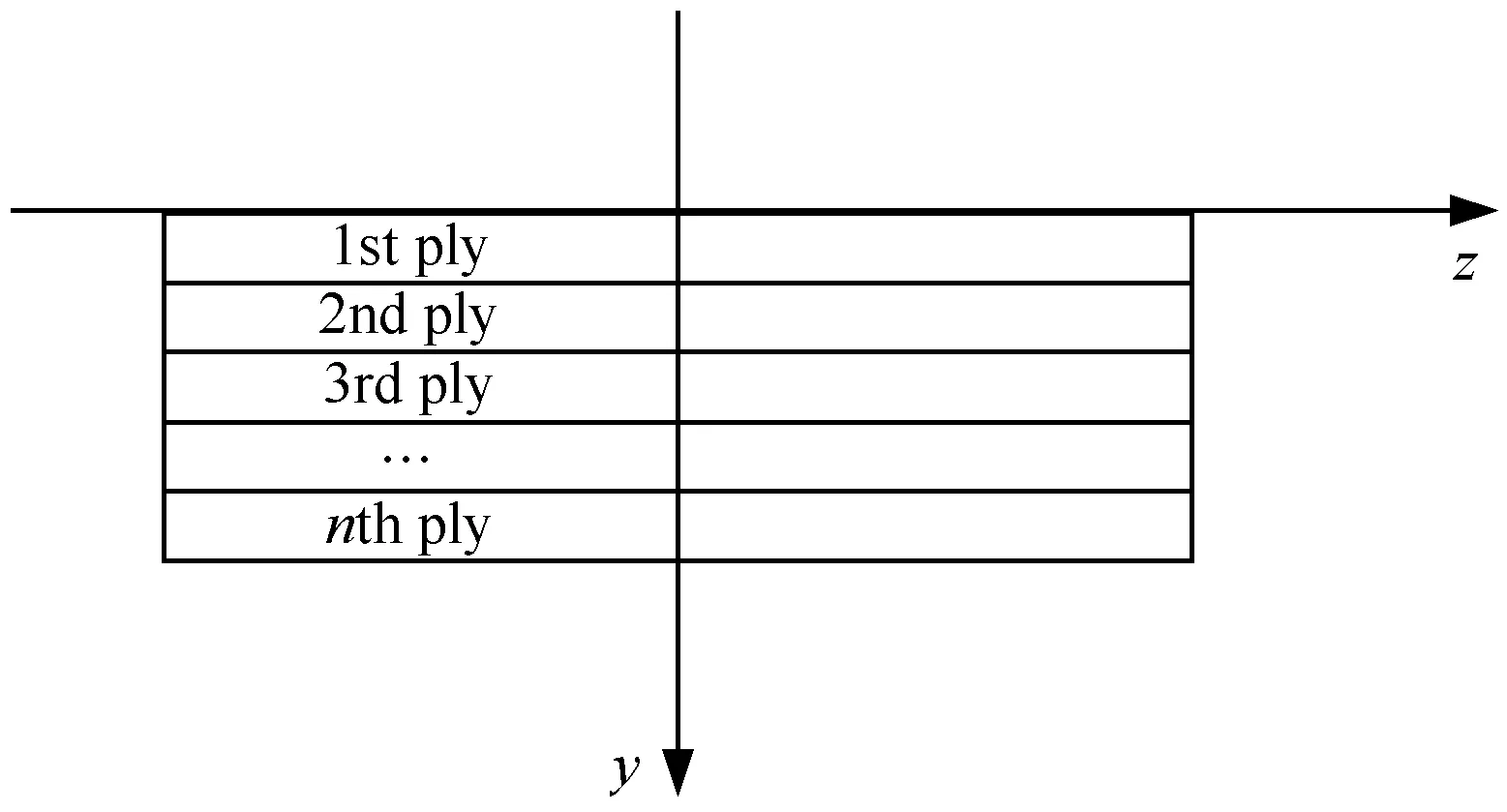
圖2 單片層合板鋪層示意圖Fig.2 Layer diagram of a single laminate plate

1.1 平衡控制方程的推導

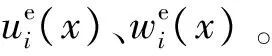
在位移沿厚度方向線性分布的假設下，單片層合板第i層位移場可以表示為

(1)

另外由于位移場沿厚度方向線性分布，u1i、w1i、u2i、w2i與層合板上下表面位移u1(x)、w1(x)、u2(x)、w2(x)應該滿足

(2)

式中：yi為第i個界面的y軸坐標；h為單片層合板厚度。

第i層應變的表達式為

(3)

一般性各向異性材料本構方程為

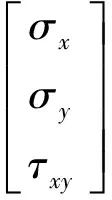
(4)

式中：c1～c6為復合材料力學參數。

將式(3)和式(4)代入第i層結構勢能表達式，可得

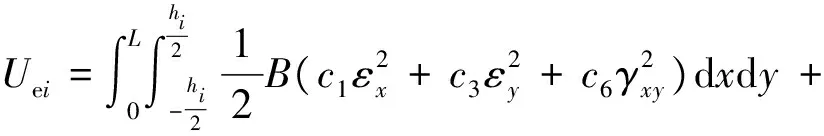
(5)

式中：B為層合板寬度；

單片層合板各層勢能組裝在一起，其結構勢能表達為

(6)

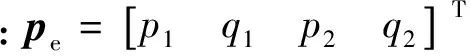
式(6)為單片層合板線性位移假設下結構勢能的表達式。如圖1所示復合材料梁，根據前述位移假設，可分別建立膠片層等各段結構勢能表達式，然后仿照有限元結構剛度矩陣的建立方法，將各層結構剛度矩陣組裝在一起，形成整體層合梁結構的勢能表達式。其中在形成腹板結構勢能表達式時，復合材料層合板材料參數同翼緣不同，腹板應采用復合材料面內材料參數，而翼緣則應采用面外材料參數。根據第1節的位移假設6),沿著高度方向將腹板共分為m段，則加上上下表面后，共有界面數為m+1，結構勢能表達式為

(7)

式中：q=[u1w1u2w2…umwm

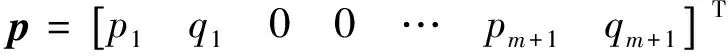
基于最小勢能原理，對層合梁結構勢能式(7)進行變分，并假設梁兩端固定，即δq=0(x=0,x=L)，可得

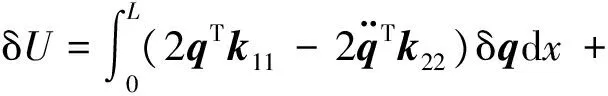
(8)

從而可得到結構的靜力平衡控制方程為

(9)

1.2 邊界條件的引入

假設層合梁兩端邊界條件為

ui(0)=0,wi(0)=0,ui(L)=0,wi(L)=0
(i=1,2,…,m+1)

可以假定位移具有下列形式：

(10)

式(10)滿足層合梁兩端的邊界條件，代入式(9)，可得

(11)

式中：

由迦遼金法[22]，式(11)兩端分別乘以sin(iπx/L) (i=1，2,…,n)，并在[0,L]區間積分，整理之后可得

K(2m+2)n×(2m+2)nA(2m+2)n×1=cp(2m+2)n×1

(12)

求解式(12)，可求得A(2m+2)n×1，即a1n、a2n、a3n、a4n、…、a(2m+1)n、a(2m+2)n，代入式(10)，即可求得層合梁各點位移。

2 復合材料層合梁自振頻率計算模型

式(5)中計入慣性力-ρu,tt的影響，可得

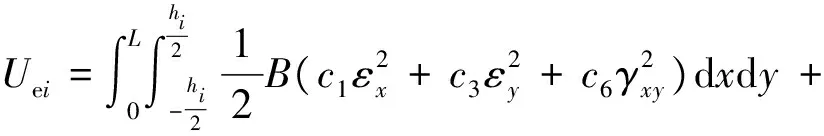
(13)

對層合梁各層組裝后，結構勢能表達式為

(14)

對式(14)進行變分，可得

(15)

假設q,tt=-ω2q，其中ω為結構自振頻率，代入式(15)可得

(16)

假設層合梁結構兩邊固定，以類似于靜力計算式(10)～式(12)的方法，可得

K(2m+2)n×(2m+2)nA(2m+2)n×1=
-ω2Km(2m+2)n×(2m+2)nA(2m+2)n×1

(17)

式(17)的求解是一個廣義特征值問題，求解其特征值，即可得到結構的自振頻率。

3 考慮橫截面剪切翹曲效應計算結果同經典梁理論計算結果的對比分析

基于式(12)與式(17)進行求解，可得到考慮橫截面剪切翹曲效應時層合梁結構靜力荷載作用下的位移響應以及結構的自振頻率。本文針對圖3和圖4所示的層合梁(兩端固定)進行計算。

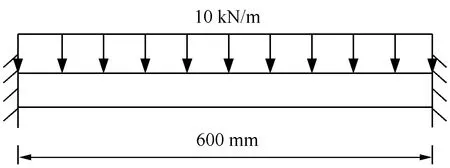
圖3 計算結構簡圖Fig.3 Structural calculation diagram

圖4 層合梁橫斷面Fig.4 Cross section of the beam

3.1 本文算法與有限元計算結果比較驗證

首先為驗證本文計算模型的合理性，分別采用本文算法以及Nastran通用有限元計算軟件對含膠層層合梁進行計算分析。在有限元計算模擬過程中，為保證分析的精確性，采用三維單元劃分有限元網格，三維有限元網格如圖5所示。

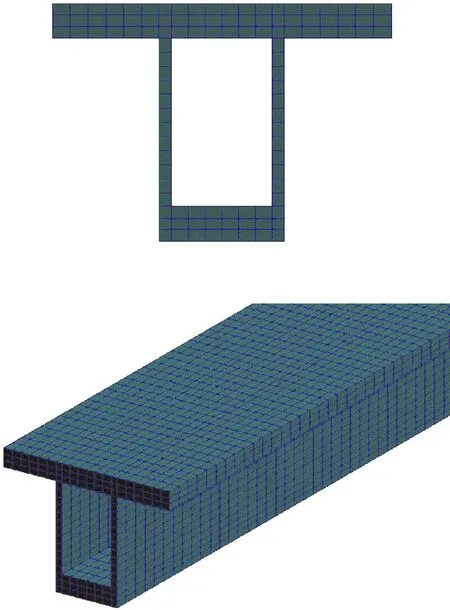
圖5 梁橫斷面及單元局部放大圖Fig.5 Cross section and partial enlargement of the element of beam

計算中假設膠層、翼緣其他層以及腹板等材料為各向同性材料。膠層的力學參數假設為：泊松比為0.3，彈性模量為5 000 MPa，膠層厚度為2 mm。翼緣其他層以及腹板材料的力學參數假設為：泊松比為0.2，彈性模量為60 000 MPa，各層厚度相等，為2.1 mm。腹板高度hw=30 mm。在以上參數基礎上分別采用本文建立的算法(Analytical Model)以及有限元模型(FE Model)對層合梁進行計算得到梁撓度曲線如圖6所示。

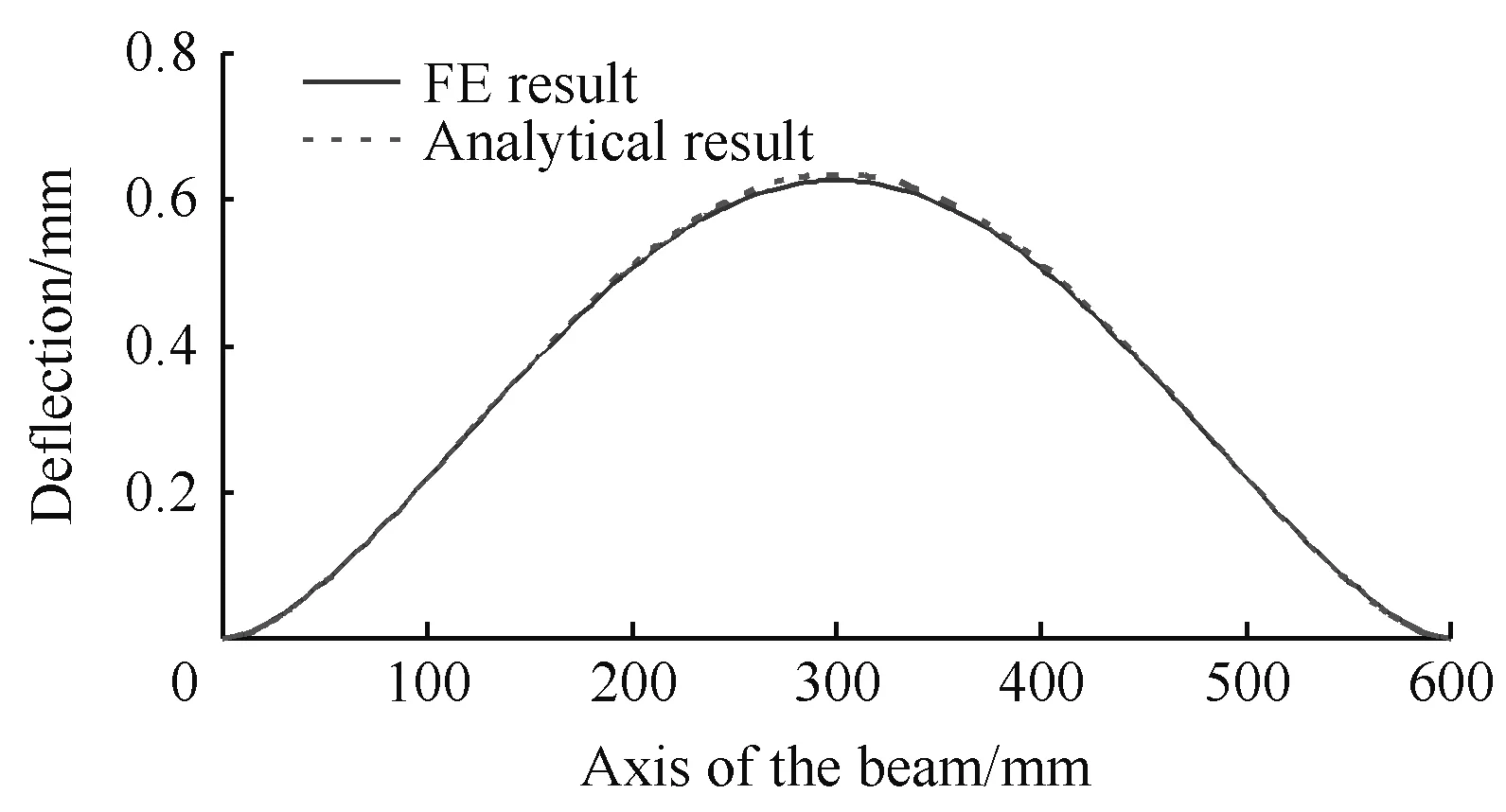
圖6 本文模型以及有限元模型計算得到的梁撓度曲線比較Fig.6 Comparison of deflection curves of beam based on model presented in this paper and FE model

由于有限元模型采用精細的三維單元進行計算，因此有限元計算結果充分考慮了層合梁的腹板剪切以及弱膠層的層間剪切影響。從圖6可以看出，本文模型計算得到的梁撓度曲線同有限元模型計算得到的梁撓度曲線基本重合，這驗證了考慮剪切翹曲效應的本文模型的正確性，因此本文模型的計算結果是可靠的。

3.2 弱膠層層間剪切影響因素分析

假設層合梁各部分的層合板為相同材料、相同鋪層，翼緣與腹板位置層合板剪切模量不同。層合梁上層頂部作用著均布荷載p=10 kN/m，其余表面荷載為0，在此工況下分別采用本文提出的考慮橫截面剪切翹曲效應的算法和經典梁理論計算結構靜力荷載作用下的位移響應和結構的自振頻率，探討膠層力學參數、截面幾何參數等因素對結構響應的影響。

3.2.1 膠層較強時橫截面翹曲對結構響應的影響

計算中假設翼緣以及腹板層合板采用相同鋪層[0°/90°/0°/90°/0°/90°/0°]，每層厚度均為0.3 mm。假設翼緣層合板材料屬性在0°方向為

腹板層合板材料屬性在0°方向為

膠層材料屬性：膠層泊松比為0.3，彈性模量E=5 600 MPa。在這種假設下，膠層剪切模量同復合材料剪切模量相當，從而在排除膠層影響的情況下分析是否考慮橫截面剪切翹曲效應兩個模型之間的差別。經典梁理論定義為模型1，考慮橫截面剪切翹曲效應定義為模型2。分別采用兩個模型編程計算，得到層合梁跨中位移以及層合梁的第1自振周期，如圖7和圖8所示。圖7和圖8的橫坐標是腹板高度；圖7的縱坐標是兩個模型跨中中點位移相對誤差((模型2-模型1)/模型1)，圖8的縱坐標是兩個模型的第1自振周期相對誤差((模型2-模型1)/模型1)。

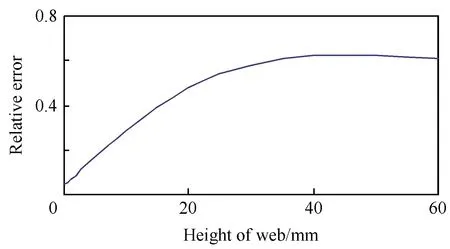
圖7 兩種計算模型跨中位移對比圖(E=5 600 MPa)Fig.7 Comparison of the midpoint displacement based on the two models (E=5 600 MPa)

圖8 兩種計算模型第1自振周期對比圖(E=5 600 MPa)Fig.8 Comparison of the first vibration cycle based on the two models (E=5 600 MPa)

由圖7和圖8可以看出，隨著腹板高度的增加，兩個模型的計算誤差也隨之增大。由于在計算中，采取的膠層剪切模量同復合材料剪切模量相當，因此基本可以排除弱膠層對計算結果的影響。兩個模型誤差隨腹板高度增大的主要原因在于，當腹板高度增加時，橫截面剪切翹曲增大，因而采用經典梁理論計算誤差會隨之增大。

3.2.2 膠層較弱時橫截面翹曲對結構響應的影響

假設復合材料層合板材料屬性以及鋪層順序不變，膠層泊松比為0.3，彈性模量E=20 MPa，這種材料假設是很典型的含弱膠層層合梁。假設腹板高度在0～60 mm之間變化，計算得到層合梁跨中位移以及層合梁的第1自振周期如圖9和圖10所示。

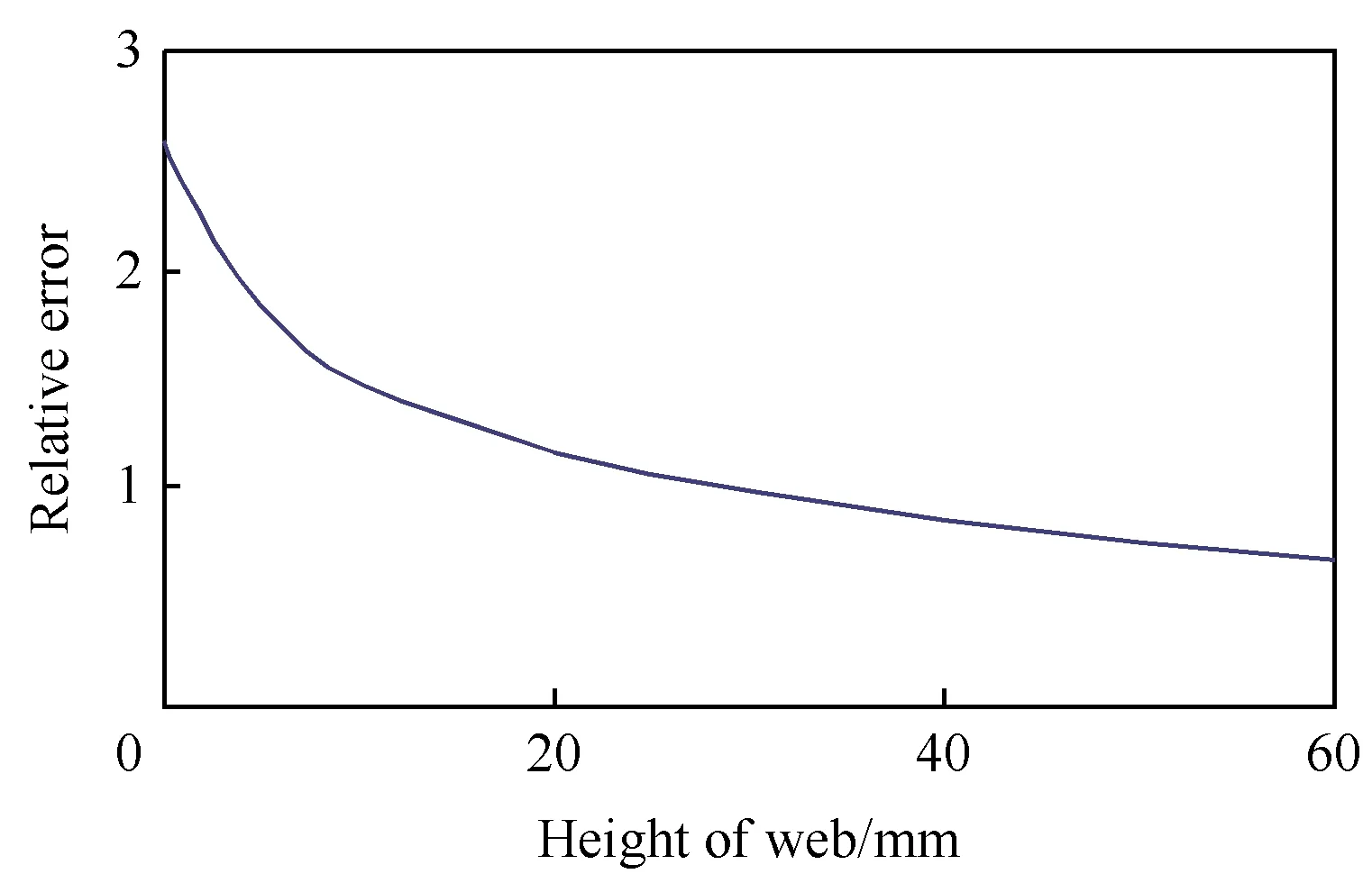
圖9 兩種計算模型跨中位移對比圖(E=20 MPa)Fig.9 Comparison of the midpoint displacement based on the two models (E=20 MPa)

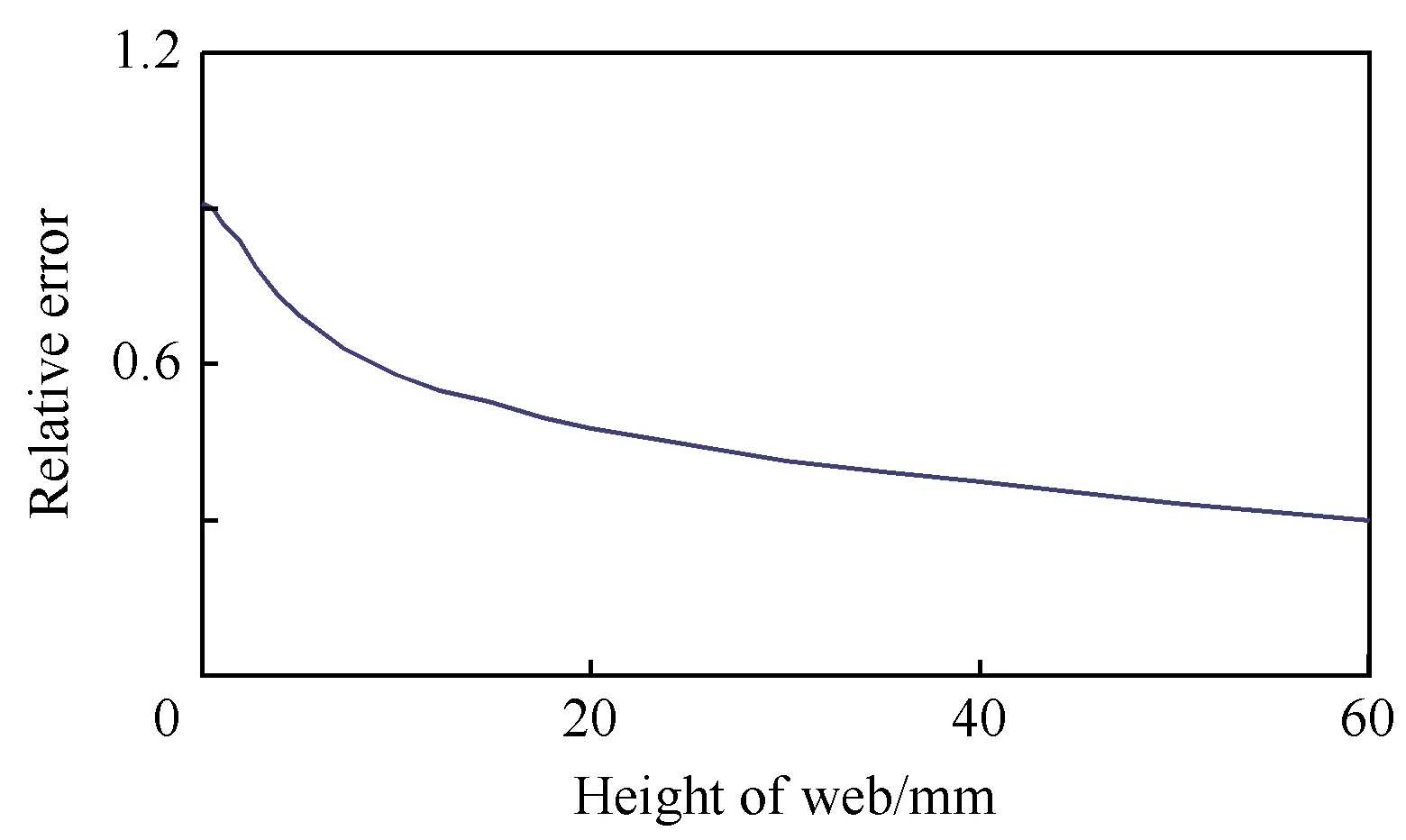
圖10 兩種計算模型第1自振周期對比圖(E=20 MPa)Fig.10 Comparison of the first vibration cycle based on the two models (E=20 MPa)

由圖9和圖10可以看出，隨著腹板高度的增加，兩種計算模型的誤差逐漸減少，同圖7和圖8的變化趨勢相反。其主要原因在于當膠層較弱時，膠層的層間剪切效應影響顯著。當腹板高度較小時，翼緣承擔的剪力相對較大，膠層的層間剪切效應也相對較大。此時橫截面剪切翹曲效應主要體現在翼緣膠層界面的層間剪切上。由圖9和圖10的計算結果可以看出，當翼緣存在弱層(如膠層)時，經典梁理論的計算結果誤差很大，此時應當采取分層位移場的方法進行計算。

3.2.3 膠層彈性模量對結構響應的影響

假設復合材料層合板材料屬性以及鋪層順序不變，腹板高度固定為15 mm，膠層泊松比固定為0.3，其彈性模量在10～5 000 MPa之間變化，計算得到層合梁跨中位移以及層合梁的第1自振周期如圖11和圖12所示。

圖11 兩種計算模型跨中位移對比圖(hw=15 mm)Fig.11 Comparison of the midpoint displacement based on the two models (hw=15 mm)

圖12 兩種計算模型第1自振周期對比圖(hw=15 mm)Fig.12 Comparison of the first vibration cycle based on the two models (hw=15 mm)

由圖11和圖12的計算結果可以看出，在膠層彈性模量低于1 000 MPa時，兩個模型的計算誤差對膠層彈性模量的取值非常敏感，其主要原因在于：當膠層較弱時，膠層的層間剪切效應顯著；而隨著膠層性能增強，膠層的層間剪切效應逐漸減小，兩個模型的計算誤差也隨之減小。

4 結 論

當層合梁翼緣存在膠層等弱層時，層合梁結構幾何參數、膠層力學參數等對層合梁性能有顯著的影響：

1) 當翼緣膠層較強，膠層界面層間剪切效應不顯著時，經典梁理論計算誤差相對較小，但計算誤差會隨著截面高度的增加逐漸增大。由于復合材料剪切模量通常比彈性模量低20～30倍，因此復合材料梁的剪切效應比普通梁大得多。因此當截面高度較大時，僅僅考慮一階剪切效應的經典梁理論計算誤差較大，此時應考慮層合梁的高階剪切效應對結構響應的影響。

2) 當翼緣膠層較弱，膠層界面層間剪切效應顯著時，不應采用經典梁理論進行計算，而應在分層位移場假設基礎上進行計算。

3) 隨著翼緣膠層彈性模量的增加，膠層界面層間剪切效應逐漸減小。當膠層是為了粘結復合材料層合板增加層合梁剛度時，應盡可能采用高彈性模量膠層；當復合材料梁是作為夾膠玻璃等支撐框架時，夾膠玻璃中的弱膠層、玻璃與梁之間的弱膠層對復合材料梁的性能影響較大，應采用分層位移場假設進行計算。

[1] Wang Y X. Design of composite structure. Beijing: Chemical Industry Press, 2001.(in Chinese)

王耀先. 復合材料結構設計．北京：化學工業出版社， 2001.

[2] Whitney J M，Sun C T．A higher order theory for extensional motion of laminated composites． Journal of Sound and Vibration, 1973, 30(1)： 85-97.

[3] Reddy J N. A simple higher-order theory for laminated composite plates. Journal of Applied Mechanics, 1984, 51(4): 745-752.

[4] Stein M. Nonlinear theory for plates and shells including the effect of transverse shearing. Journal of AIAA, 1986, 24(9): 1537-1544.

[5] Kwon Y W, Akin J E. Analysis of layered composite plates using a higher-order deformation theory. Computers and Structures, 1987, 27(5): 619-623.

[6] Fu X H, Chen H R, Wang Z M. A refined higher-order theory and its finite element method for thick laminated plates. Acta Materiae Compositae Sinica, 1992, 9(2): 39-46.(in Chinese)

傅曉華， 陳浩然， 王震鳴. 復合材料多層厚板精化高階理論及其有限元法. 復合材料學報， 1992， 9(2)： 39-46.

[7] Li X Y, Liu D．Generalized laminated theories based on double superposition hypothesis．International Journal of Numerical Methods Engineering, 1997, 40(7): 1197-1212.

[8] Chandra R, Stemple A D, Chopra I. Thin-walled composite beams under bending, torsional and extensional loads. Journal of Aircraft, 1990, 27(7): 619-636.

[9] Jeon S M, Cho M H, Lee I. Static and dynamic analysis of composite box beams using large deflection theory. Computers & Structures, 1995, 57(4): 635-642.

[10] Wu Y P, Zhu Y L, Lai Y M, et al. Analysis of shear lag and shear deformation effects in laminated composite box beams under bending loads. Composite Structures, 2002, 55(2): 147-156.

[11] Vo T P, Lee J. Flexural-torsional behavior of thin-walled closed-section composite box beams. Engineering Structure, 2007, 29(8): 1774-1782.

[12] Wu Y P, Wang X J, Su Q, et al. A solution for laminated box beams under bending loads using the principle of complementary energy. Composite Structures, 2007, 79(3): 376-380.

[13] Vo T P, Lee J. Geometrically nonlinear analysis of thin-walled composite box beams. Computers and Structures, 2009, 87(3-4): 236-245.

[14] Vo T P, Lee J. Interaction curves for vibration and bucking of thin-walled composite box beams under axial loads and end moments. Applied Mathematical Modelling, 2010, 34(10): 3142-3157.

[15] Chakrabarti A, Sheikh A H, Griffith M, et al. Analysis of composite beams with partial shear interactions using a higher order beam theory. Engineering Structures, 2012, 34(3): 283-291.

[16] Rodman U, Saje M, Planinc I, et al. Exact buckling analysis of composite elastic columns including multiple delaminations and transverse shear. Engineering Structures, 2008, 30(6): 1500-1514.

[17] Han H T, Zhang Z, Lu Z X. Analytical method on bending of composite laminated beams with delaminations. Applied Mathematics and Mechanics, 2010, 31(7): 843-852.(in Chinese)

韓海濤， 張錚， 盧子興． 含分層復合材料層合梁彎曲問題的一般解法． 應用數學與力學, 2010, 31(7): 843-852.

[18] Aslan Z, Sahin M. Buckling behavior and compressive failure of composite laminates containing multiple large delaminations. Composite Structures, 2009, 89(3): 382-390.

[19] Kim C, White S R. Analysis of thick hollow composite beams under general loading. Composite Structures, 1996, 34(3): 263-277.

[20] Kim C, White S R. Thick-walled composite beam theory including 3-D elastic effects and torsional warping. International Journal of Solids Structure, 1997, 34(31-32): 4237-4259.

[21] Zhong W X. The new solution system of elastic mechanics. Dalian: Dalian University of Technology Press, 1995.(in Chinese)

鐘萬勰．彈性力學求解新體系．大連：大連理工大學出版社， 1995.

[22] Wang X C. Finite element method. Beijing: Tsinghua University Press, 2003.(in Chinese)

王勖成．有限單元法．北京： 清華大學出版社， 2003.

AnalysisofthePerformanceofaBeamMadeofCompositeMaterialswithaGlueLayer

WANGDongfang,YANGJialing*

SchoolofAeronauticScienceandEngineering,BeihangUniversity,Beijing100191,China

Becausetheshearmodulusofacompositematerialisusuallyfarlessthanitselasticmodulus,shearresponseplaysagreatroleintheperformanceofabeammadeofcompositematerials,especiallyinthecaseofabeamwithlargesectionheight.Whenasquarepipebeammadeofcompositematerialssupportsastructuremembersuchasaglass-glue-glassstructure,thereisaweakergluelayerinthemiddleofthebeamflange.Inthiscase,complexwarpingwillbeproducedinthebeamcrosssectionbecauseofshearing.Basedonthepiecewiselineardisplacementfieldtheory,calculationmodelsofstaticanalysisandself-vibrationfrequencyaresetupforasquarepipebeammadeofcompositematerialsanddeformedwithinthesymmetryplane,andtheresultsarecomparedwiththosefromclassictheory.Thecalculationresultsinthispaperprovethatthegeometryparametersofthebeamandthemechanicalparametersofthegluelayerhavegreateffectontheperformanceofthebeam;inparticular,whentheglueisbyfarweakerthanthecompositematerial,theglueplaysadominantrole，andinthissituationtheclassicbeamtheoryisnotapplicable.

squarepipebeam;compositematerial;cross-sectionwarping;gluelayer;piecewiselinearity

2012-03-14；Revised2012-04-10；Accepted2012-04-24；Publishedonline2012-07-111704

URL：www.cnki.net/kcms/detail/11.1929.V.20120711.1704.003.html

NationalNaturalScienceFoundationofChina(11032001)

.Tel.：010-82317528E-mailJLYang@buaa.edu.cn

2012-03-14;退修日期2012-04-10;錄用日期2012-04-24; < class="emphasis_bold">網絡出版時間

時間：2012-07-111704

www.cnki.net/kcms/detail/11.1929.V.20120711.1704.003.html

國家自然科學基金(11032001)

.Tel.：010-82317528.EmailJLYang@buaa.edu.cn

WangDF,YangJL.Analysisoftheperformanceofabeammadeofcompositematerialswithagluelayer.ActaAeronauticaetAstronauticaSinica,2012,33(9):1655-1663. 王東方，楊嘉陵. 含膠層復合材料梁構件性能分析. 航空學報，2012,33(9):1655-1663.

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

1000-6893(2012)09-1655-09

V414.8

A

王東方男， 博士研究生。主要研究方向： 沖擊動力學。

Tel: 010-82338796

Email： east9235@163.com

楊嘉陵男， 博士， 教授， 博士生導師。主要研究方向： 沖擊動力學。

Tel: 010-82317528

Email： JLYang@buaa.edu.cn