突變理論及PLS模型在城市缺水程度評價中的應用
李三平 徐 強
(1.浙江省水文局蘭溪水文站,浙江 金華321100;2.浙江省金華市水文站,浙江 金華 321013)
1 突變原理
1.1 突變模型
該理論認為,在某一發展變化過程中,事物常常會從一個狀態跳躍式地變到另一個狀態,或經過緩慢、連續的變化,會產生一種不連續的變化,即突變現象的發生。突變理論能直接處理不連續性問題、而不聯系其任何特殊的內在機制和規律。
突變理論歸納出若干個初等突變模型,一般的突變模型是指Rene.Thom歸納的7個初等突變模型。常用有尖點突變、燕尾突變和蝴蝶突變(皆為一個狀態變量)。
1.2 突變理論歸一公式
通過分解形式的分歧方程導出歸一公式,歸一公式將系統內部各控制變量的不同質態規劃為可比較的同一種質態,即用狀態變量表示的質態。運用歸一公式,可求出表征系統狀態特征的系統總突變隸屬函數值,即利用突變理論進行綜合分析評判的基本運算公式。常用的三中突變模型的歸一公式:
尖點突變:

燕尾突變:
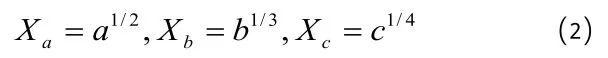
蝴蝶突變:
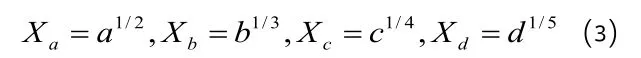
在歸一公式中,狀態變量X及諸控制變量皆取0~1范圍的數值。突變級數法規定,必須遵循“越大越好”原則的準則模型體系,方可用歸一模型計算。如果n個控制變量的矛盾關系是均衡的,則求得的狀態變量X的值為n個控制突變級數之和除以n,而不用歸一公式計算。

表1 缺水程度等級狀態
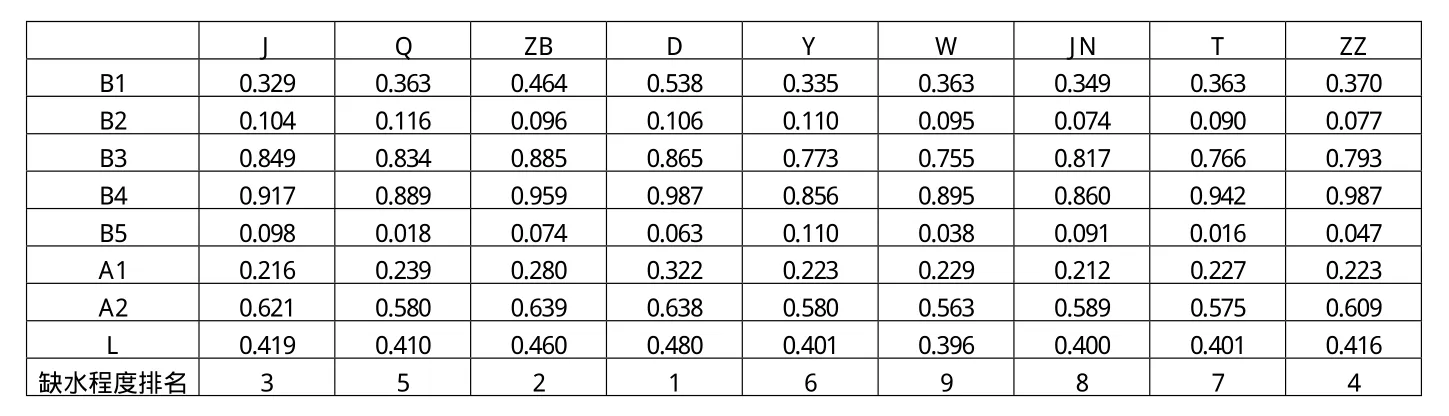
表2 評價結果表
2 山東9個主要城市總體評價
2.1 缺水程度初始綜合值和調整綜合值的計算
建模所用山東9個重點城市為濟南(J)、青島(Q)、淄博(ZB)、東營(D)、煙臺(Y)、濰坊(W)、濟寧(JN)、泰安(T)、棗莊(ZZ)。
借鑒洪災危險程度的劃分,將缺水程度進行等級劃分,見表1;
以1995年山東省9個重點城市的數據資料為基礎(源自1995年山東統計年鑒),評價其1995年水資源緊缺程度,結果見表2。
分析評價結果,計算出的綜合值將在0到1之間變化,綜合評價值越大,則城市的缺水程度越高,反之則越低。
據圖,山東9城市缺水程度水平屬輕險,其中東營的缺水程度最高,其次為淄博、濟南,而濰坊水資源相對最豐富。
2.2 PLS回歸模型
建立山東省缺水程度L與Ci(i=1.2…5)指標因素之間的PLS模型,得到影響L的最主要因素,從而改善山東缺水狀況。
主成分分析:據兩個主成分的散點圖,樣本點均落在T2橢圓內,故模型無特異點,不需要剔除數據,模型判斷參數R2Y(cum)=0.992,表明模型擬合數據較好,見圖2。
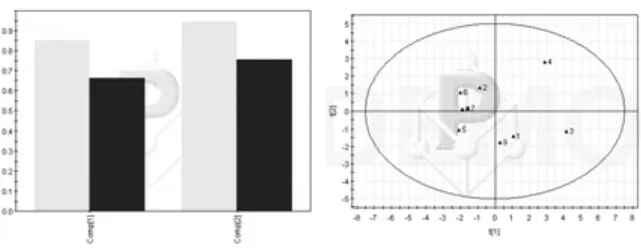
圖2 主成分分析及特異點檢驗圖
C1、C2、C4、C6、C8、C11的相關系數與實際相反,原因上述指標在山東9個重點市所占指標比重相差較大,故剔除不考慮。C9與L成負相關,且相關系數最大,說明水資源利用率對山東缺水程度影響最大,水資源利用率提高,缺水程度將大幅降低。
結語
(1)山東9個重點城市的缺水程度水平L較接近,均屬于輕險,其中東營缺水程度最高L=0.480,淄博、濟南次之,而濰坊缺水程度相對較低,L=0.396。
(2)水資源利用率)和單位GDP需水量對缺水程度L影響最大,降低缺水程度最好措施為增加研究區水資源利用率與降低單位GDP的需水量。
(3)突變理論的評價方法的特點在于,重要性的確定量化是根據其影響因素之間的關系采用歸一公式進行的,避免了帶有主觀性的權重賦值,而且計算公式簡單明了。
(4)PLS模型可以在數據較少時建立回歸模型,避免變量間的多重共線性。
[1]都興富.突變理論在經濟領域的應用[M].成都:電子科技大學出版社,1994.
[2]改進的突變評價法在旱災風險評價中的應用[M].上海交通大學出版社,1987.第一章.
[3]Poston T, Lan Stewant.Catastrophe theory and application[M].Lord: Pitman,1978.Chapter1
[4]楊杰,胡德秀,吳中如.大壩安全監控模型因子相關性及不確定性研究[J].水利學報,2004,12:99-105.

