應(yīng)變天平矩形截面元件扭轉(zhuǎn)應(yīng)變計(jì)算準(zhǔn)度分析

胡國(guó)風(fēng)

（中國(guó)空氣動(dòng)力研究與發(fā)展中心，四川 綿陽 621000）

0 引 言

在風(fēng)洞測(cè)力試驗(yàn)中，通過測(cè)量彈性元件表面應(yīng)變來確定作用在模型上空氣動(dòng)力的測(cè)力裝置稱為應(yīng)變天平。圖1是典型的彈性元件橫截面形狀為矩形的桿式應(yīng)變天平結(jié)構(gòu)，對(duì)其在扭矩作用下的應(yīng)變分析，目前大都是基于材料力學(xué)“桿件”的扭轉(zhuǎn)變形理論。材料力學(xué)中，所謂“桿件”是指長(zhǎng)度尺寸（L）“遠(yuǎn)大于”橫向尺寸（b、h）的構(gòu)件。由于小型化應(yīng)變計(jì)的成功應(yīng)用和提高天平整體結(jié)構(gòu)剛度的需要，矩形截面彈性元件的“長(zhǎng)度”尺寸大都在10～20mm 范圍。因此，上述矩形截面彈性元件基于“桿件”的假設(shè)條件并不總是能夠滿足的。這就導(dǎo)致基于材料力學(xué)“桿件”扭轉(zhuǎn)變形理論得出的應(yīng)變計(jì)算值與天平實(shí)際校準(zhǔn)得出的應(yīng)變值相比產(chǎn)生較大的誤差，這一誤差有時(shí)可達(dá)近80%，這一情況給天平設(shè)計(jì)者帶來了困難。因此，有必要對(duì)應(yīng)變天平矩形截面元件扭轉(zhuǎn)應(yīng)變計(jì)算準(zhǔn)度進(jìn)行研究。

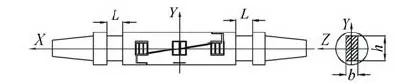
圖1 彈性元件橫截面形狀為矩形的典型桿式應(yīng)變天平Fig.1 Sting strain gauge balance with rectangular cross-section

1 分析方法

1.1 工程方法

習(xí)慣上將基于傳統(tǒng)的材料力學(xué)理論來設(shè)計(jì)應(yīng)變天平的方法稱為工程方法。采用工程方法計(jì)算圖1所示應(yīng)變天平的輸出應(yīng)變時(shí)有一個(gè)重要假設(shè)條件，即將與彈性元件相連的天平體視為剛體。基于這一假設(shè)條件，在分析其扭轉(zhuǎn)應(yīng)變時(shí)，為分析簡(jiǎn)便起見，可將圖1所示的模型簡(jiǎn)化為圖2所示的分析模型。

如圖3 所示，當(dāng)矩形截面元件在扭轉(zhuǎn)力矩作用下，各橫截面變形后不再保持平面，形成翹曲。但若各橫截面翹曲程度均相同，則所有縱向纖維的長(zhǎng)度均未改變，橫截面上將沒有正應(yīng)力而只有切應(yīng)力，這種情況稱為自由扭轉(zhuǎn)或純扭轉(zhuǎn)。矩形截面桿自由扭轉(zhuǎn)時(shí)，橫截面上的切應(yīng)力分布如圖3所示，最大切應(yīng)力發(fā)生在橫截面長(zhǎng)邊中點(diǎn)處，其方向與長(zhǎng)邊相切，4 個(gè)角點(diǎn)處的切應(yīng)力均等于零。產(chǎn)生自由扭轉(zhuǎn)的條件是：等直桿兩端僅受力偶作用，桿的各橫截面可以自由翹曲。這在實(shí)際中是很少的，大多數(shù)桿件由于受到約束，例如一端固定的桿，扭轉(zhuǎn)時(shí)各橫截面翹曲的程度就不相同，因而橫截面上還有正應(yīng)力，這種扭轉(zhuǎn)稱為約束扭轉(zhuǎn)。但對(duì)于矩形、橢圓形等截面實(shí)心桿來說，在約束扭轉(zhuǎn)時(shí)所產(chǎn)生的正應(yīng)力一般數(shù)值較小，可以略去不計(jì)。

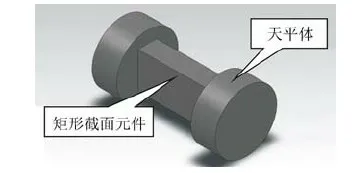
圖2 矩形截面元件扭轉(zhuǎn)應(yīng)變分析模型Fig.2 Analysis model for the torsion strain of the component with rectangular cross section

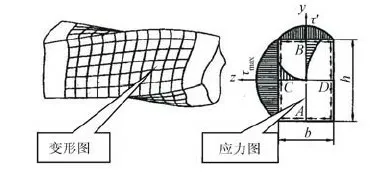
圖3 矩形截面元件扭轉(zhuǎn)時(shí)的變形圖與應(yīng)力圖Fig.3 Distortion and stress of the component with rectangular cross section for the rolling moment

為了測(cè)量扭轉(zhuǎn)力矩，在矩形截面長(zhǎng)邊的中心處沿與天平x軸45°方向上粘貼應(yīng)變計(jì)，根據(jù)梁在受扭轉(zhuǎn)時(shí)45°方向的主應(yīng)力與最大剪應(yīng)力相等的原理來測(cè)量天平受到的扭矩。具體計(jì)算公式如下：

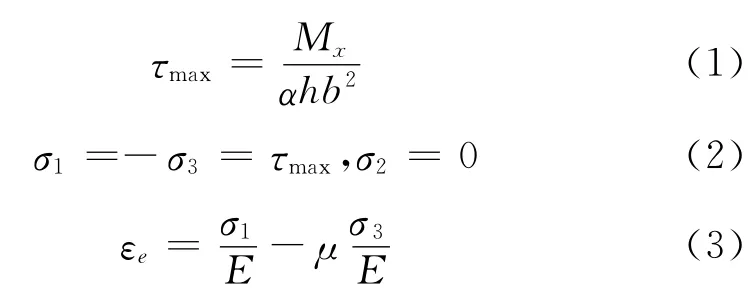
其中：Mx為扭轉(zhuǎn)力矩，α是與矩形截面長(zhǎng)短邊之比有關(guān)的系數(shù)，h和b為矩形截面的長(zhǎng)短邊（h≥b），τmax為矩形截面長(zhǎng)邊中點(diǎn)處的最大切應(yīng)力，σi（i=1，2，3）是矩形截面長(zhǎng)邊的3個(gè)主應(yīng)力，μ和Ε為天平材料的泊松比和彈性模量，εe矩形截面長(zhǎng)邊中點(diǎn)處采用工程方法計(jì)算獲得的應(yīng)變值。

1.2 數(shù)值仿真方法

應(yīng)變天平數(shù)值仿真的具體步驟如下：（a）利用SolidWorks2010軟件建立研究對(duì)象的三維有限元分析模型（圖2）；（b）采用SolidWorks2010軟件自帶的simulation插件進(jìn)行網(wǎng)格劃分（圖4）；（c）給定約束條件（左端固定），利用simulation插件的“遠(yuǎn)程載荷”功能施加扭矩載荷，進(jìn)行有限元計(jì)算；（d）利用simulation插件獲得矩形截面長(zhǎng)邊的中心處沿與天平x軸成45°方向上的應(yīng)變（εf）輸出大小。

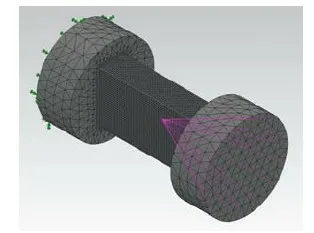
圖4 矩形截面元件扭轉(zhuǎn)應(yīng)變分析模型網(wǎng)格Fig.4 Grids of the analysis model of the component with rectangular cross section

1.3 天平校準(zhǔn)方法

根據(jù)應(yīng)變天平的校準(zhǔn)結(jié)果，可以反推出該天平的最大輸出應(yīng)變?chǔ)與，方法如下：

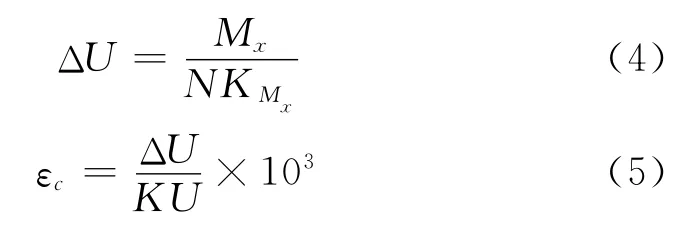
其中：N為天平Mx分量測(cè)量電橋的數(shù)量，KMx為天平Mx分量校準(zhǔn)的主項(xiàng)系數(shù)，ΔU為天平Mx分量的滿量程輸出電壓，K為應(yīng)變計(jì)的靈敏度系數(shù)（K=1.9～2.1，取K=2.0），U為Mx分量測(cè)量電橋的激勵(lì)電壓。

2 分析過程

研究目標(biāo)是以扭轉(zhuǎn)應(yīng)變數(shù)值仿真結(jié)果εf為基準(zhǔn)，分析矩形截面元件的“長(zhǎng)度”尺寸L對(duì)扭轉(zhuǎn)應(yīng)變工程方法計(jì)算結(jié)果εe準(zhǔn)度的影響。因此，實(shí)驗(yàn)參數(shù)有：矩形截面的長(zhǎng)短邊之比m=h／b和矩形截面梁的長(zhǎng)度與長(zhǎng)邊之比k=L／h。實(shí)驗(yàn)過程如下：

（a）確定m變化序列為：1.00、1.20、1.50、1.75、2.00、2.50、3.00、4.00、5.00、10.00；

（b）選定h=30mm，根據(jù)m變化序列確定相應(yīng)的b值大小；

（c）確定k變化序列為：0.33、0.5、0.67、0.83、1、2、3、4、5，那么對(duì)應(yīng)的矩形截面梁長(zhǎng)度尺寸L序列為：10、15、20、25、30、60、90、120和150mm；

（d）從m變化序列中選取m，變化k，分別采用工程方法和數(shù)值仿真方法獲得矩形截面元件的扭轉(zhuǎn)應(yīng)變?chǔ)舉和εf；

（e）應(yīng)變計(jì)算誤差分析：

（f）繪制δ～k（k=L／h）曲線。

天平材料牌號(hào)為00Ni18Co8Mo5TiAl（代號(hào)F141），其彈性模量E=1.8725×1011N／m2、抗剪模量G=6.664×1010N／m2、泊松比μ=0.4049。

3 結(jié)果及分析

εe和εf的計(jì)算誤差δ隨著k的變化規(guī)律δ～k曲線如圖5所示。由此可見：

（a）當(dāng)k＞2時(shí)，無論何種截面長(zhǎng)短邊比m，εe與εf的一致性都較好，兩者誤差在5%以內(nèi)，說明基于材料力學(xué)“桿件”扭轉(zhuǎn)變形理論得出的扭轉(zhuǎn)應(yīng)變計(jì)算公式（1）～（3）的計(jì)算結(jié)果滿足工程實(shí)際需要；

（b）當(dāng)k≤2時(shí)，隨著應(yīng)變梁長(zhǎng)度L的縮短，εe與εf的差異越來越大，且其誤差δ隨著m的增大而增大（最大誤差可達(dá)近80%），說明基于材料力學(xué)“桿件”扭轉(zhuǎn)變形理論得出的扭轉(zhuǎn)應(yīng)變計(jì)算公式（1）～（3）的計(jì)算結(jié)果不滿足工程實(shí)際需要；

（c）特別地，對(duì)于正方形截面（m=1.00），當(dāng)0.67≤k≤2時(shí)，εe與εf的一致性仍然較好，兩者誤差在5%以內(nèi)，說明此時(shí)基于材料力學(xué)“桿件”扭轉(zhuǎn)變形理論得出的扭轉(zhuǎn)應(yīng)變計(jì)算公式（1）～（3）的計(jì)算結(jié)果仍滿足工程實(shí)際需要。

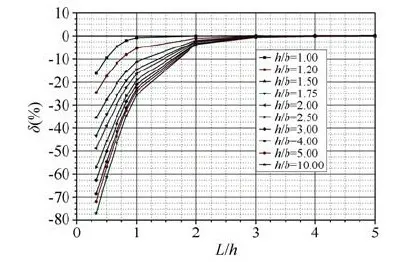
圖5 扭轉(zhuǎn)應(yīng)變計(jì)算準(zhǔn)度誤差曲線Fig.5 Error curves of the torsion strain

4 驗(yàn)證算例

4.1 驗(yàn)證算例一

圖6所示是中國(guó)空氣動(dòng)力研究與發(fā)展中心低速所研制的一臺(tái)典型矩形截面的桿式六分量應(yīng)變天平數(shù)值計(jì)算分析模型（1，332，012個(gè)節(jié)點(diǎn)，961，854個(gè)單元，3，994，035個(gè)自由度）。該天平有關(guān)參數(shù)如下：天平材料為F141，扭轉(zhuǎn)力矩為Mx=6000N·m，矩形截面梁長(zhǎng)度L=25mm、長(zhǎng)邊h=90mm、短邊b=50mm，α=0.240。該天平Mx分量測(cè)量電橋?qū)嶋H激勵(lì)電壓為U=17.829V，測(cè)量電橋數(shù)量為N=2，校準(zhǔn)主項(xiàng)系數(shù)為KMx=172.7N·m／mV。那么：

（a）m=1.80，k=0.28；

（b）根據(jù)式（1）～（3），可得該天平扭轉(zhuǎn)應(yīng)變工程計(jì)算結(jié)果為εe=832.2（με）；

（c）根據(jù)1.2節(jié)所述方法，可得該天平扭轉(zhuǎn)應(yīng)變數(shù)值仿真結(jié)果為εf=473.0（με）；

（d）根據(jù)式（4）～（5）可得該天平扭轉(zhuǎn)應(yīng)變校準(zhǔn)結(jié)果為εc=487.2（με）；

（e）根據(jù)圖5所示，采用線性插值的方法，可以預(yù)知εe與εf的誤差應(yīng)在-45%左右。

據(jù)此可進(jìn)一步分析該天平Mx分量扭轉(zhuǎn)應(yīng)變各種方法的計(jì)算誤差：

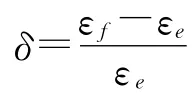
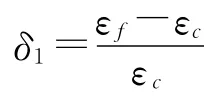
由此可見，該天平扭轉(zhuǎn)應(yīng)變?chǔ)舉與εf的計(jì)算誤差δ大小與圖5所給分析結(jié)果相差2%左右，具有較好的一致性；εf與εc的結(jié)果具有較好的一致性。

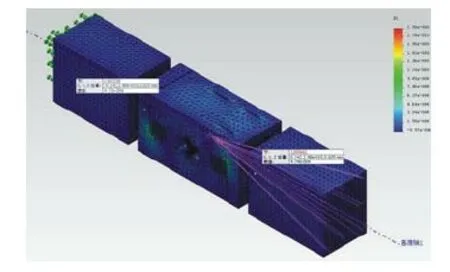
圖6 驗(yàn)證算例一分析模型Fig.6 Analysis model of the validated exampleⅠ

4.2 驗(yàn)證算例二

圖7所示是中國(guó)空氣動(dòng)力研究與發(fā)展中心低速所研制的一臺(tái)典型矩形截面的桿式六分量應(yīng)變天平數(shù) 值 計(jì) 算 分 析 模 型（403，755 個(gè) 節(jié) 點(diǎn)，276，386 個(gè) 單元，1，207，329個(gè)自由度）。該天平有關(guān)參數(shù)如下：天平材料為F141，扭轉(zhuǎn)力矩為Mx=22.653N·m，矩形截面梁長(zhǎng)度L=15mm、長(zhǎng)邊h=17mm、短邊b=8.5mm，α=0.246。該天平Mx分量測(cè)量電橋?qū)嶋H激勵(lì)電壓為U=8.051V，測(cè)量電橋數(shù)量為N=1，校準(zhǔn)主項(xiàng)系數(shù)為KMx=2.857Nm／mV。那么：

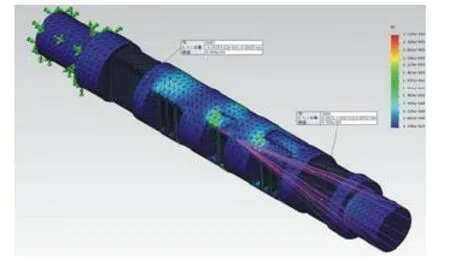
圖7 驗(yàn)證算例二分析模型Fig.7 Analysis model of the validated exampleⅡ

（a）m=2.00，k=0.88；

（b）根據(jù)式（1）～（3），可得該天平扭轉(zhuǎn)應(yīng)變工程計(jì)算結(jié)果為εe=562.5（με）；

（c）根據(jù)1.2節(jié)所述方法，可得該天平扭轉(zhuǎn)應(yīng)變數(shù)值仿真結(jié)果為εf=492.0（με）；

（d）根據(jù)式（4）～（5）可得該天平扭轉(zhuǎn)應(yīng)變校準(zhǔn)結(jié)果為εc=492.4（με）；

（e）根據(jù)圖5所示，采用線性插值的方法，可以預(yù)知εe與εf的誤差應(yīng)在-19%左右。

據(jù)此可進(jìn)一步分析該天平Mx分量扭轉(zhuǎn)應(yīng)變各種方法的計(jì)算誤差：

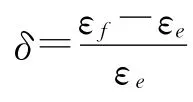
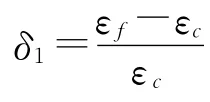
由此可見，該天平扭轉(zhuǎn)應(yīng)變?chǔ)舉與εf的計(jì)算誤差δ與圖5所給分析結(jié)果相差6.5%左右，具有較好的一致性；εf與εc的結(jié)果具有很好的一致性。

5 結(jié) 論

綜上所述，可以得出以下結(jié)論：

（a）矩形截面扭轉(zhuǎn)應(yīng)變數(shù)值仿真結(jié)果εf與實(shí)際校準(zhǔn)結(jié)果εc具有較好的一致性，且其差異程度與m和k的大小無關(guān)；

（b）矩形截面扭轉(zhuǎn)應(yīng)變工程計(jì)算結(jié)果εe與數(shù)值仿真結(jié)果εf（或?qū)嶋H校準(zhǔn)結(jié)果εc）的差異程度與k的大小有關(guān)。具體如下：

（1）當(dāng)k＞2時(shí)，無論何種截面長(zhǎng)短邊比m，εe與εf的一致性都較好，兩者誤差在5%以內(nèi)；

（2）當(dāng)k≤2時(shí)，隨著應(yīng)變梁長(zhǎng)度L的縮短，εe與εf的差異越來越大，且其誤差δ隨著m的增大而增大，最大誤差可達(dá)近80%；

（3）特別地，對(duì)于正方形截面（m=1.00），當(dāng)0.67≤k≤2時(shí)，εe與εf的一致性仍然較好，兩者誤差在5%以內(nèi)。

［1］ 賀德馨.風(fēng)洞天平［M］.北京：國(guó)防工業(yè)出版社，2001.

［2］ 李慶華.材料力學(xué)［M］.成都：西南交通大學(xué)出版社，2005.