2.4m 跨聲速風洞顫振試驗流場控制技術研究

芮 偉，易 凡，杜 寧，秦建華

（中國空氣動力研究與發展中心，四川 綿陽 621000）

0 引 言

顫振是飛行器上出現的一種破壞性振動，一旦飛行速壓超過臨界值，振幅就迅速增大，它是在氣動力、彈性力和慣性力作用下的自激振動，是從氣流中吸取能量的結果。由于顫振的危害性，故飛行器在飛行包線內絕對不允許出現顫振現象［1］。為了評估飛行器安全飛行的顫振包絡線，需要在2.4m 跨聲速風洞（以下簡稱：2.4m 風洞）建立顫振試驗技術。它對風洞提出了兩種流場控制方式。方式一：定馬赫數階梯變速壓的試驗方式，即保持馬赫數為定值，通過逐步增加試驗段氣流總壓的方法增加速壓，逐步逼近顫振臨界速壓，甚至增加到模型出現顫振。該方式要求其啟動過程速壓平滑上升，總壓超調小于0.5kPa，一次啟動要完成4個以上盡可能多的速壓階梯，在出現險情時，具有自動平穩關車的能力，速壓按要求的速率下降。該方式適用于臨界速壓范圍比較寬的情況。方式二：定總壓線性變馬赫數方式，即固定總壓，通過連續、線性地增加馬赫數，逐漸提高總壓（密度），切割顫振臨界速壓隨馬赫數變化曲線，獲取顫振臨界速壓。該方式適用于臨界速壓對馬赫數變化比較敏感的情況。在實際應用中，組合使用兩種方式可以獲得較好的試驗效果。結合暫沖式風洞的特點，為拓展風洞試驗能力，采用基于運動規律法的定馬赫數階梯變速壓智能控制策略和基于運動函數的定總壓線性變馬赫數控制策略，實現了顫振試驗流場控制，滿足了試驗要求。

1 2.4m 跨聲速風洞流場控制模型

2.4m 風洞用于流場建立的控制系統包括主引射器調壓閥控制系統、主排氣閥穩定段總壓控制系統、柵指馬赫數控制系統、駐室流量閥馬赫數控制系統和駐室引射器調壓閥控制系統。受風洞閉合回路的影響，風洞穩定段總壓和馬赫數可表示為式（1）［2］。從模型中可以發現2.4m 風洞是一個多輸入兩輸出的多變量控制系統。

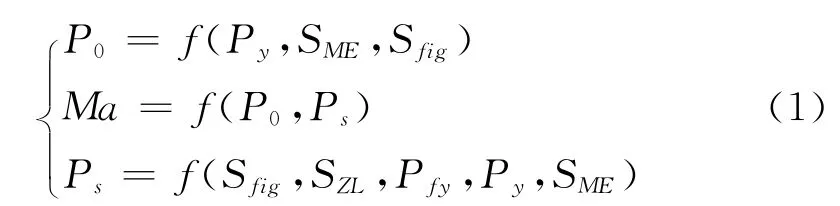
式中，P0為穩定段總壓（MPa）；Ps為穩定段總壓（MPa）；Ma為試驗段馬赫數；Py為主引射器引射壓力（MPa）；Sfig為柵指位移（mm）；SZL為駐室流量閥位移（mm）；Pfy為輔引射器引射壓力（MPa）；SME為主排位移（mm）。

2 技術要求和難點

（1）定馬赫數階梯變速壓試驗工況的技術要求：

·馬赫數試驗范圍0.3～1.2；

·一次車總壓試驗范圍105～450kPa，總壓的階梯跨度可高達150kPa以上；

·在啟動過程中，速壓平滑上升，且要求各階梯總壓調節過程不得超過下一階梯總壓設定值，由于總壓階梯最小變化量為0.5kPa，即總壓調節過程的超調量以0.5kPa為限；

·在出現險情時，具有自動平穩關車的能力，即關車時總壓下降要均勻、速度要受控；

·一個啟動要完成4個以上盡可能多的速壓階梯。

（2）定總壓線性變馬赫數試驗工況的技術要求：

·馬赫數試驗范圍0.3～1.2；

·總壓試驗范圍105～450kPa。

（3）定馬赫數階梯變速壓試驗工況的技術難點：

結合2.4m 風洞的特點，確定采用定馬赫數階梯變總壓的方式來實現定馬赫數階梯變速壓的試驗工況。由于2.4m 風洞是一個多輸入兩輸出的多變量控制系統，其風洞流場控制存在強非線性、強耦合以及控制參數之間大滯后的多變量調節特性。同時，整個流場控制過程分成啟動充壓、流場調節、變總壓以及關車等四個控制環節。啟動充壓環節主要實現風洞從無風狀態到首個總壓階梯變化的調節過程，涉及到“三個切換”，即主調由控制總壓到控制主引壓力的切換、主排由位置閉環到總壓閉環的切換、柵指和駐流由位置閉環到馬赫數閉環的切換，且系統之間存在著相互耦合以及大滯后等問題，使得整個啟動過程的控制難度增大；流場調節環節主要實現總壓和馬赫數的精確調節，涉及柵指和駐流的閉環控制；變總壓環節主要實現從當前總壓到目標總壓的變化過程，涉及總壓、主引壓力的協同變化控制；關車環節主要是實現總壓平穩下降，使該過程成為涉及主引射壓力、總壓的多變量控制過程。其中，流場調節環節和變總壓環節交替切換進行。

（4）定總壓線性變馬赫數試驗工況的技術難點：馬赫數線性變化過程，涉及到柵指、駐流對馬赫數變化的快速跟隨問題。

3 定馬赫數階梯變速壓方式

2.4m 風洞是一個非線性、強耦合、大時滯的多變量控制系統，總壓處于工作點附近時可采用線性化控制策略，而總壓的大跨度調節過程為強非線性的暫態過程，為縮短總壓的調節時間同時減小超調，可采用模糊算法和智能分段變PI相結合的方法，即總壓大階梯變化時，根據運動規律法的特征，采用模糊算法將該過程分為多個調節段，各段則根據誤差和誤差變化率智能選擇調節參數，當誤差變化到一定范圍內則采用智能分段變PI控制器實現對總壓的精確調節。其中，運動規律法主要是采用偏差e和偏差變化速度來決定控制模態，在（e-）相平面上理想的相軌跡如圖1所示。其中，偏差e1由系統固有特性決定。在實時控制中，偏差e1可直接取為設定值變化量Δyr，e4和為滿足控制精度要求的偏差和偏差變化速度。整個變化過程分為四部分：第一部分：e1→e2段是勻減速運動，采用Bang-Bang控制策略激發出較大偏差變化速度；第二部分：e2→e3段是勻速運動，采用保持較大偏差變化速度的控制策略，盡量減小偏差；第三部分：e3→e4段是勻加速運動，采用直接壓低較大偏差變化速度的控制策略，避免產生超調，達到控制精度要求的范圍；第四部分：e4→原點是勻加速運動，系統已運行到控制精度要求的范圍，采用保持控制量的策略。利用運動規律可得到系統在每一段的運行時間和控制律［3］。設計智能控制器最困難的問題是如何選擇控制模態切換閾值，因此，采用模糊算法實現分段。整個變速壓方式實質上是設計了一個由暫態控制器和穩態控制器組成的控制器，解決了設定值跟蹤和抑制負載干擾的矛盾。暫態控制器采用運動規律法進行設計，適用于大滯后過程，適用于啟動充壓、變總壓以及關車等調節環節，具有極好的設定值跟蹤能力。穩態控制器采用智能分段PI控制器，適用于流場調節環節，保證了控制器在設定值附近具有良好的調節效果的同時，還具有良好的抑制干擾的能力，如圖2。

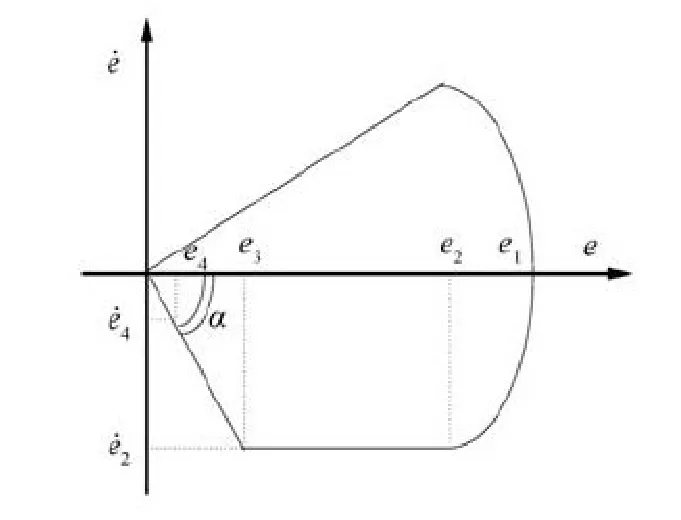
圖1 理想相軌跡Fig.1 Sketch of ideal phase track

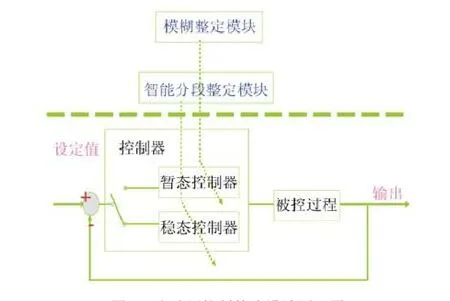
圖2 變速壓控制策略設計原理圖Fig.2 Sketch of control tactics in adjusting dynamical pressure

4 定總壓線性變馬赫數方式

在2.4m 風洞中，主要是通過控制柵指和駐室流量閥的位置來實現馬赫數的精確控制。控制方式包括純柵指控制、純駐室流量閥控制、固定駐室流量閥+柵指控制和固定柵指+駐室流量閥控制等4種方式。其中，Ma≤0.9 適用于純柵指控制方式，0.9＜Ma≤1.1適用于固定駐室流量閥+柵指控制和固定柵指+駐室流量閥控制方式，1.1＜Ma≤1.2適用于純駐室流量閥控制。因此，根據2.4m 風洞的實際情況，按照馬赫數調節方式和最低啟動壓力，設計了基于運動函數的定總壓線性變馬赫數控制策略。主要思想是：啟動風洞，建立流場到起始馬赫數Ma0，然后以一定的馬赫數變化率V1，來給定馬赫數的值，待到達目標馬赫數Ma1后，保持馬赫數的調節狀態。如圖3。其運動函數如式（2）。在馬赫數變化過程中，由于設定馬赫數與反饋馬赫數之間偏差較小，通過整定PID 參數可以確保在設定值附近具有良好的調節效果。

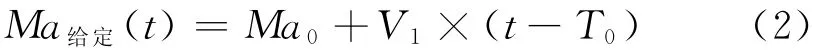
圖3 定總壓線性變馬赫數原理圖Fig.3 Sketch of adjusting Mach number

5 實際應用效果

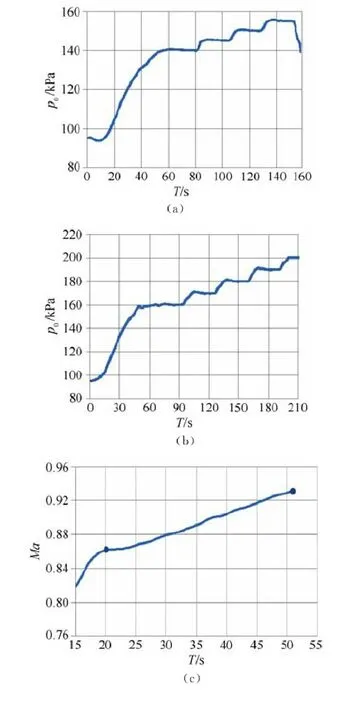
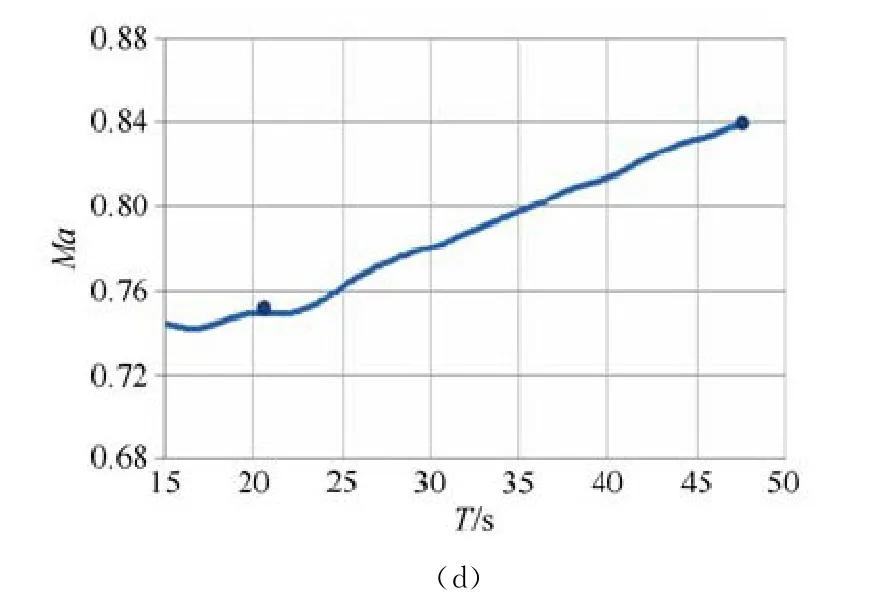
圖4 試驗曲線Fig.4 Curves of Test

2001年以來，先后完成了變速壓和線性變馬赫數兩種試驗工況的設計工作，初步在2.4m 風洞建立了顫振試驗流場控制平臺，通過數百次的各類型號試驗證明，該項試驗技術達到了預期的設計效果，受到型號單位的好評。曲線如圖4。其中，圖4（a）和圖4（b）為變速壓曲線，圖4（a）的試驗條件為：馬赫數1.1，總壓階梯為140、145、150和155kPa，穩態過程的總壓精度控制在0.5%以內，關車過程總壓按設定的速率下降至安全區；圖4（b）的試驗條件為：馬赫數0.7，總壓階梯為160、170、180、190和200kPa，總壓超調小于0.5kPa，在一次啟動中實現了多階梯大跨度的變速壓試驗條件，耗氣量滿足試驗要求。圖4（c）和（d）為線性變馬赫數曲線，圖4（c）的馬赫數變化范圍為0.86～0.94，圖4（d）的馬赫數變化范圍為0.75～0.84，馬赫數在設定區域內實現線性變化，沒有出現超調和波動的情況，滿足了試驗要求。

6 結 論

結果表明：

（1）基于運動規律法的變速壓控制策略和基于運動函數的線性變馬赫數控制策略，滿足了顫振試驗的要求，具有快速、準確、可靠的試驗效果。

（2）穩態過程的總壓精度達到0.5%，馬赫數控制精度0.005，馬赫數試驗范圍0.3～1.2。

（3）風洞啟動時，速壓上升曲線比較平滑，總壓超調量小于0.5kPa。

（4）風洞關車過程實現了總壓以任意設定斜率下降至安全區的功能。

（5）在線性變馬赫數試驗中，馬赫數在設定區域內實現線性變化。

［1］ 惲起麟.實驗空氣動力學［M］.北京：國防工業出版社，1994.

［2］ 施洪昌.高低速風洞測量與控制系統設計［M］.北京：國防工業出版社，2001.

［3］ PELA A F.Closed-loop Mach number control in a transonic wind-tunnel［J］.AIAA Jounal，1989，30：25-32.

［4］ 趙娟平.神經網絡PID 控制策略及其Matlab仿真研究［J］.微計算機信息，2007，23（3）：59-60.

［5］ 廖芳芳，肖建.基于BP神經網絡PID 參數自整定的研究［J］.系統仿真學報，2005，17（7）：1711-1713.

［6］ 杜寧.2.4m 風洞顫振試驗調試總結報告［R］.中國空氣動力研究與發展中心，2008.