基于相對斜率的改進灰色關聯度模型研究
馬引弟
(陜西理工學院數學與計算機科學學院,陜西 漢中 723000)
基于相對斜率的改進灰色關聯度模型研究
馬引弟
(陜西理工學院數學與計算機科學學院,陜西 漢中 723000)
通過對現有灰色關聯度模型的研究,依據數據序列時點間相對斜率差來計算關聯系數,以灰色關聯系數均值的修正值作為序列的關聯度,提出了改進的灰色關聯度模型,并研究了改進模型的性質。研究表明,利用該方法所得分析結果與定性分析相一致,且分辨效果更好,因而具有可行性。
灰色關聯度;相對斜率;穩定度
灰色關聯分析是灰色系統理論的重要組成部分,其主要通過系統數據序列曲線的幾何形狀的相似和相近程度,用量化的方法判斷序列間關聯程度的大小,曲線越接近,形狀越相似,相應序列間的關聯度越大,反之越小。目前有關關聯度的量化模型很多[1-6],這些模型從不同角度考慮了曲線相似性的衡量問題,在社會經濟和生產實踐中取得了一定的應用效果,但也存在各種缺陷,如容易受到數據極值和采樣數據質量的影響、不滿足整體性公理、不能反映序列間的正負相關性、不滿足規范性和保序性、沒有考慮到穩定性等。為此,筆者從分析事物發展規律的角度出發,提出了一種改進的灰色關聯度模型。該模型以系統數據序列中相鄰時點間的相對斜率差作為計算灰色關聯系數的依據,引入符號函數來反映序列的正負相關關系,利用點關聯系數序列穩定度[7]的概念來計算關聯度,并討論了改進模型的性質,最后通過實例驗正了該方法的實用性。
1 改進的灰色關聯度模型及性質
1.1改進灰色關聯度模型的建立
建立改進灰色關聯度模型的基本思路如下:采用序列中相鄰時點間的相對斜率差的兩極最大和最小差,綜合考慮系統中比較序列對關聯系數的影響,用灰色關聯系數來衡量序列的局部相似性,以其均值表示2序列的整體相似度,最后利用點關聯系數序列的穩定度對整體相似度進行修正,從而得到改進的灰色關聯度。
具體計算方法如下:
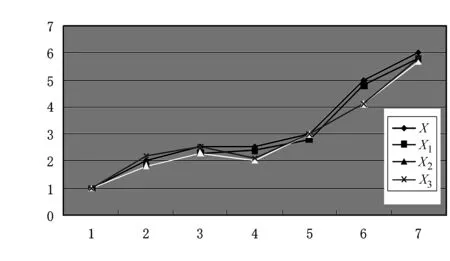
設時間區間[a,b],0≤a 定義1設區間[a,b]上的系統特征序列為X={x(t1),x(t2),…x(tn)},系統行為序列為Xi={xi(t1),xi(t2),…xi(tn)}(i=1,2,…m),稱: (1) 為X與Xi在時點t到時點t+Δt的灰色關聯系數,ρ∈[0,1],其中: 注:當X與Xi(i=1,2,…m)均為1-時距離散序列時,X與Xi在時點t到時點t+Δt的灰色關聯系數為: (2) (3) 稱S(ξi)為序列X與Xi的點關聯系數序列的穩定度。S(ξi)越大,點關聯系數序列穩定性越差。 為序列X與Xi的改進灰色關聯度。 1.2改進灰色關聯度模型的性質 性質2具有整體性; 性質4具有保序性,即對原始序列進行無量綱化處理,不會改變灰色關聯度的值。 因無量綱化處理對點灰色關聯系數的計算沒有影響,而灰色關聯度的計算考慮的是點關聯系數的整體穩定性,故不會改變灰色關聯度的值。 圖1 數據序列的折線圖 采用文獻[4]的算例,設參考序列X=(1,2,2.5,2.5,3,5,6),比較序列如下: X1=(1,1.8,2.3,2.4,2.8,4.8,5.8) X2=(1,1.8,2.3,2,3,4.1,5.7) X3=(1,2.2,2.5,2.1,3,4.1,5.8) 數據序列的折線圖如圖1所示,計算結果如表1所示。 從圖1可以看出,各比較序列相鄰時點間斜率與參考序列相鄰時點間斜率的接近情形:序列X1與參考序列最接近,序列X2,X3與參考序列的差異要大一些,且X2,X3與參考序列的近似程度相差不多。 表1 關聯度的比較 結合圖1的分析,從表1可以看出,鄧氏灰色關聯度與實際情況不符,而改進模型以時點間相對斜率差作為灰色關聯系數的計算依據,考慮了序列各時點的正、負相關關系,并從整體上消除了點關聯系數的顯著差異對關聯度的影響。序列X1與參考序列在各時點間的相對斜率差異小,序列X2、X3與參考序列的差異大,同時在某些時點間X2、X3與參考序列相交,改進模型考慮了序列間的這些差異,正確反映了比較序列與參考序列相近程度的次序,所得結果與定性分析相一致,和實際情況是相符的。 在鄧氏灰色關聯度和灰色斜率關聯度的基礎上,建立了一種基于時點間相對斜率差的改進灰色關聯度模型。該模型從分析事物發展規律的角度,綜合考慮了整體性對關聯度的影響,能夠反映序列各時點的正、負相關關系,且不受無量綱變換處理的影響,并有效地解決點關聯系數具有顯著差異下的關聯度計算問題。算例分析表明,改進后的模型所得結果與定性分析相一致,分辨效果清晰。該模型在一定程度上改進了灰色關聯度模型的性能,拓寬了灰色關聯度的應用范圍,具有良好的實用性。 [1]鄧聚龍.灰色系統的基本方法[M].武漢:華中理工大學出版社,1987. [2]梅振國.灰色絕對關聯度及其計算方法[J].系統工程,1992,10(5):43-44. [3]魏麗,陳麗宇.關于一類新的廣義灰色關聯度[J].寧夏大學學報(自然科學版),2007,28(1):22-24. [4]王靖程,諸文智,張彥斌.基于面積的改進灰色關聯度算法[J].系統工程與電子技術,2010,32(4):777-779. [5]黨耀國,劉思峰,劉斌,等.灰色斜率關聯度的改進[J].中國工程科學,2004,6(3):41-44. [6]單聯宏.灰色斜率關聯度的改進及應用[J].長江大學學報(自然科學版),2010,7(3):N441-443. [7]崔杰.點關聯系數有顯著差異下灰色關聯分析模型的改進[J].統計與決策,2008(24):4-6. [編輯] 李啟棟 10.3969/j.issn.1673-1409(N).2012.11.09 O29;N941 5 A 16731409(2012)11N02503


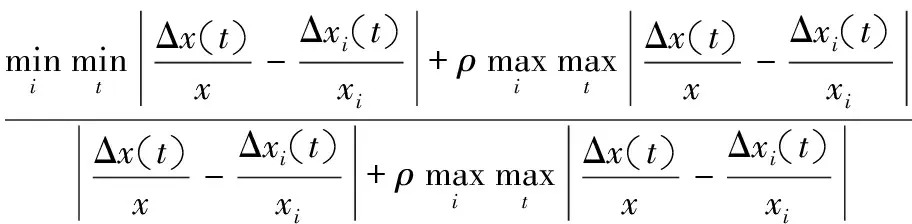
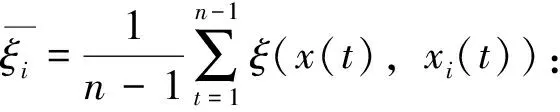
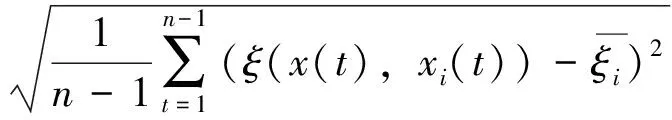
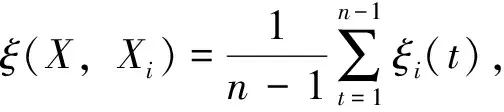




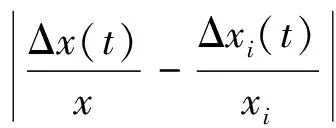
2 算例分析

3 結 語

