一類偏微分方程組解的局部穩(wěn)定性

于 海

（江海職業(yè)技術學院，江蘇 揚州 223001）

對于偏微分方程，

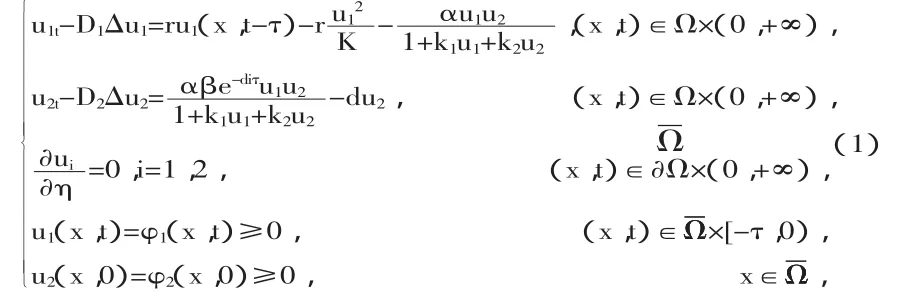
我們可利用線性化和特征值方法證明其局部穩(wěn)定性，設

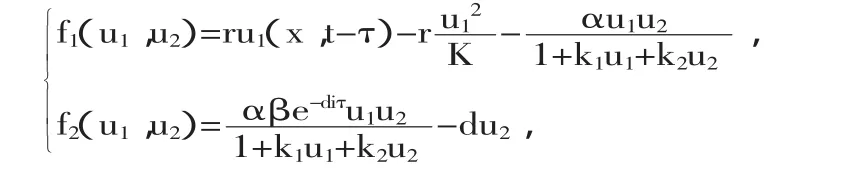
對求偏導得：

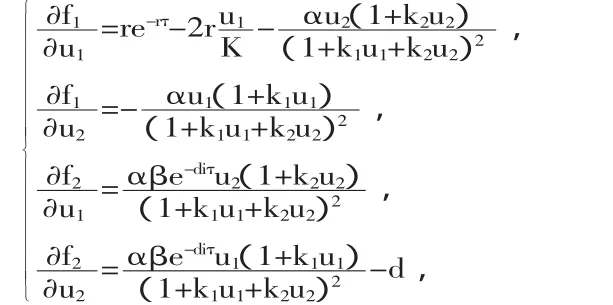
則Jacobian矩陣為：

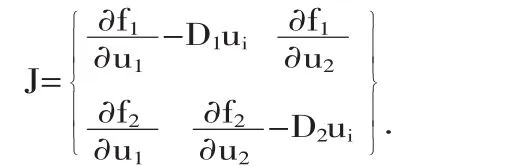
1.平凡解的局部穩(wěn)定性

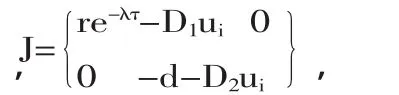
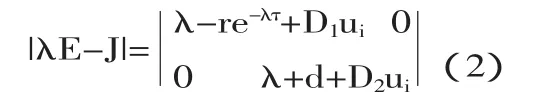
令｜λE-J｜=0，得特征根 λ1=re-λτ-D1ui，λ2=-d-D2ui.

令f（λ）=λ-re-λτ+D1ui，取ui=0，則f（λ1）=λ1-re-λ1τ，

所以由介值定理，（2）至少存在一個特征根，所以平衡點 E0=（0,0）不穩(wěn)定.

定理1系統(tǒng)（1）的平凡解E0=（0,0）不穩(wěn)定.

2.半平凡解 E1=（K，0）的局部穩(wěn)定性

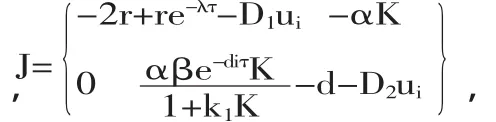
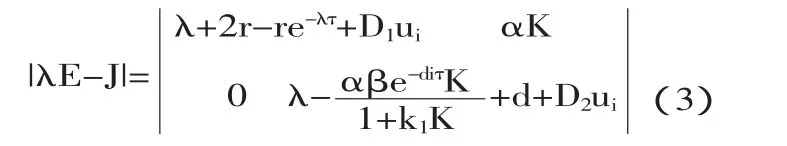
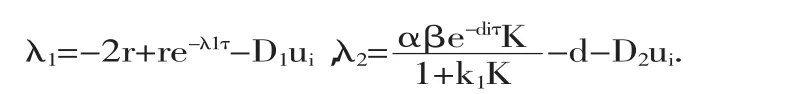
令f（λ）=λ+2r-re-λτ+D1ui，f'（λ）=1+rτe-λτ＞0，

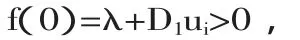
故?λ＞0，f（λ）＞f（0）＞0，

所以，f（λ）=λ+2r-re-λτ+D1ui=0無正根，即λ1非正；

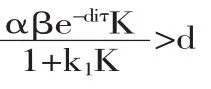
3.正平衡點E2=（u1*，u2*）的局部穩(wěn)定性

當 E2=（u1*，u2*）時，為了更簡便地得到矩陣，先引入一些記號：

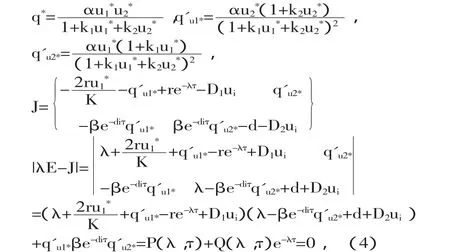
其中：

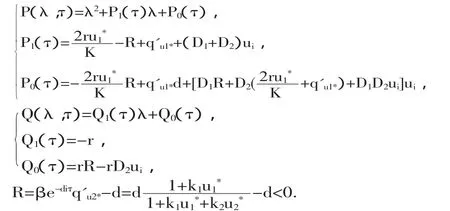
當然，特征方程（4）需在 τ∈I=[0，τ*）內討論負根的存在性.

下面我們證明對于任意的τ，λ=0不可能是特征方程（4）的解：

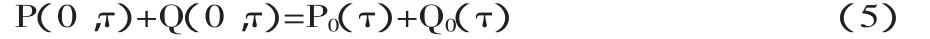
因為

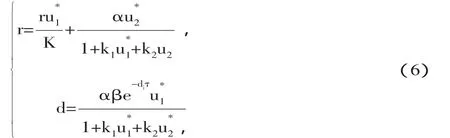
將（6）代入（5）得：

特征方程（4）在τ=0時對于任意的λ有P（λ，0）+Q（λ，0）=0，即：

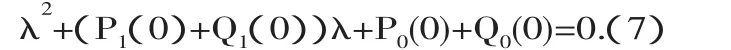
因為?τ∈I，P0(τ)+Q0(τ)＞0，所以P0(τ)+Q0(τ)＞0，

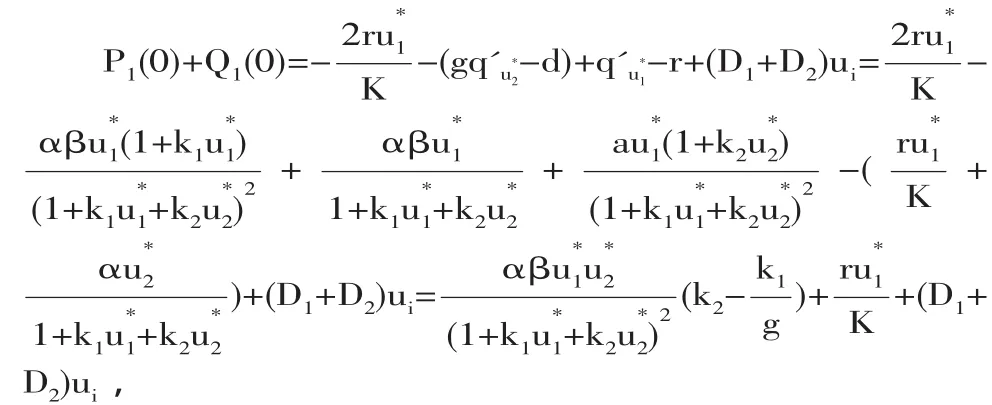
因此，我們有

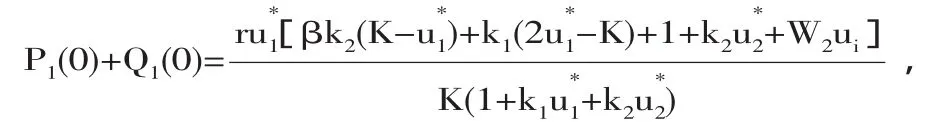
隨著τ在I=［0,τ*］內的增加，特征方程（4）有可能會出現(xiàn)一對虛根，不妨設λ=iω(τ)，ω(τ)為實部，

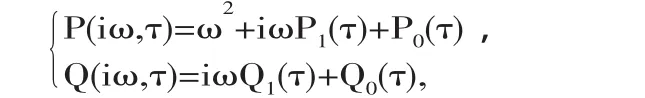
由（4）有：|P(λ,τ)|=|-Q(λ,τ)e-λτ|.

令λ=iω(τ)，得

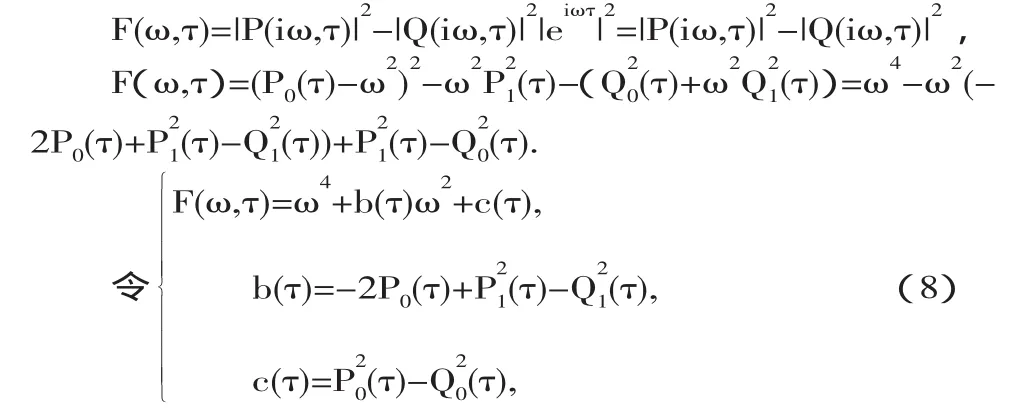
下面我們證明：

首先，證明當τ=0時的穩(wěn)定性，即考慮此時（4）在τ=0時（7）根的情況.

由（9）得：

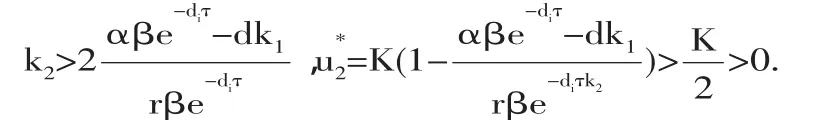
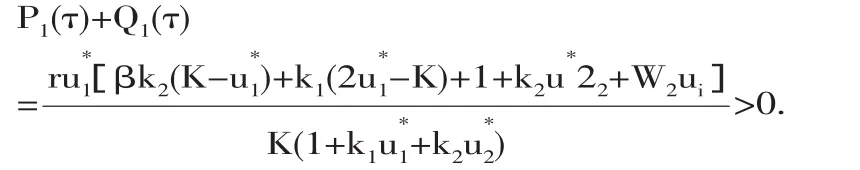
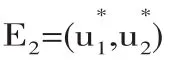
考慮方程φ(θ)=θ2+b(τ)θ+c(τ)=0（其中θ=ω2）.