自適應網格交互多模型不敏粒子濾波算法

許江湖，劉 忠，黨 玲

(1.海軍工程大學 電子工程學院，湖北 武漢430033;2.海軍大連艦艇學院，遼寧 大連116018)

0 引 言

多模型(MM)算法是機動目標跟蹤算法中一個很受歡迎的方法。其主要思想是:設計一系列的模型來代表可能的系統行為方式或結構(稱為系統模式)，基于每個模型的濾波器并行地工作，系統的整體估計則是各模型濾波器所做估計的數據融合。大多數現存的MM 估計算法，包括交互多模型(IMM)算法，在所有的時刻均使用預先確定的固定模型集合，在這個意義上是具有固定結構(FS)的。固定結構多模型(FSMM)算法存在的缺陷是［1］:為了覆蓋現實環境中的大范圍的可能的機動，算法所選的模型集合應該盡可能大。然而，增加模型的數量不但會引起計算量的增加，而且由于在當前時刻所使用的模型之間存在不一致會引起模型之間不必要的競爭，因此未必能保證跟蹤性能的提高。變結構多模型(VSMM)算法是近年來發展起來的最有效的機動目標跟蹤濾波算法，該算法能克服FSMM 算法的缺陷，且具有較高的費效比(即算法達到的性能和花費的計算量之比)。因此該算法從提出到目前，其在機動目標跟蹤應用方面一直倍受關注。然而，目前的MM 算法包括VSMM，各模型濾波算法通常采用卡爾曼濾波或者擴展卡爾曼濾波算法，對非線性、非高斯系統模型，其濾波性能將大大降低。

近年來，粒子濾波(PF)被應用于目標跟蹤，以解決其中的非線性、非高斯問題［2］。考慮到MM 算法和PF 算法二者之間的互補性，文獻［3-5］將IMM 與PF 相結合，提出了交互多模型粒子濾波算法(IMMPF)。IMMPF 由于既能跟蹤目標的機動，又不受非線性、非高斯的限制，因此該算法一經提出，國內外學者對其進行了相當多的研究和改進［6-8］。

由于上述文獻對IMMPF 的改進都沒有涉及到IMM 算法，也就是這些算法在多模型這個意義上都是具有固定結構的，因此，FSMM 算法存在的缺陷，這些算法都不可避免地存在。另外，由于標準粒子濾波算法是用系統狀態的轉移概率作為重要性密度函數，沒有利用最新量測信息，使得產生的粒子樣本經常集中在后驗概率分布的尾部，從而導致粒子選擇的盲目性，降低了濾波精度。為此，本文將一種變結構多模型算法——自適應網格交互多模型(AGIMM)算法和UPF 算法相結合，提出了自適應網格交互多模型不敏粒子濾波算法(AGIMMUPF)。該算法通過自適應網格實現了模型自適應，從而以較小的模型集合覆蓋了目標大范圍的機動，并以此來克服固定結構IMMPF 存在的缺陷，同時各模型濾波算法采用不敏粒子濾波(UPF)，使重要性密度函數融合了最新量測信息，更好地逼近真實狀態的后驗概率分布。通過計算機仿真證明，提出的算法可以有效提高IMMPF 的費效比。

1 跟蹤模型

考慮如下的隨機混合系統:

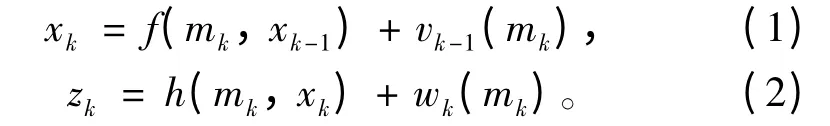
FSMM 算法(包括IMM)在每個時刻k 使用1 個預先確定的系統模型集合Mf。該模型集合要選擇等于或接近所有可能的系統模式集合M。而變結構方法建議在每個時刻k 使用根據包含在量測序列中的所有可能信息來選擇的一個時變模型集合Mk?M。其基本思想是通過使用當前起作用的模式信息來選擇包含在M 中在當前時刻可能的系統模型Mk。

2 自適應網格交互多模型不敏粒子濾波算法

2.1 AGIMM 算法簡介

AGIMM 算法［9］從1 個粗略的網格開始，然后在每個遞歸時間步根據1 個自適應邏輯對網格進行調整，從而實現模型集合自適應調整。在協同轉彎機動模型的框架內，描述模型集合的網格設為轉彎速率的連續間隔。AGIMM 算法無需事先確定候選模型集合，特別適合系統可能的模型集合很大的情況。

2.2 AGIMMUPF 算法步驟

AGIMMUPF 算法在k 時刻進行濾波之前，首先要進行網格自適應調整:根據k-1 時刻的模型概率和使用的網格(模型集合)Mk-1，計算k 時刻的網格Mk。由此可見，AGIMMUPF 算法和固定結構IMMUPF 算法最根本的區別是在AGIMMUPF 算法中，不同時刻使用的模型集合有可能不相同。由此也產生了如何為新模型分配粒子并確定其協方差的問題。解決方法是基于文獻［1］中建立起來的系統模式集合的狀態相關性的概念。簡單地講，這個概念就是給定當前系統模式，下一時刻的可能系統模式集合為由馬爾可夫規律確定的整個模式集合的1 個子集。當應用到這里的粒子分配并確定其協方差時，為新的模型最優分配粒子，僅考慮那些允許從其他模型切換到這些新模型的模型的粒子及其協方差。

具體講，新模型mj的粒子(N 為粒子數)可按如下方法得到:為得到粒子，僅使用基于模型集合Ej的粒子這里Ej為Mk-1允許切換到mj中的模型集合，其定義為:

Ej={ml:ml∈Mk-1，plj≠0}。這樣，k 時刻基于模型mj的粒子可以用類似于IMMPF 的交互步驟來完成［10］:

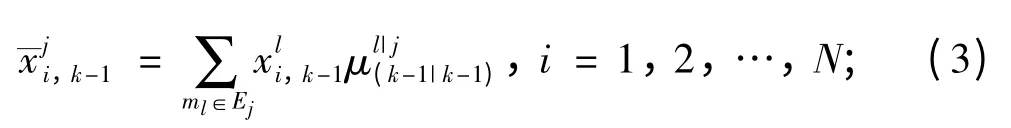
混合權重為

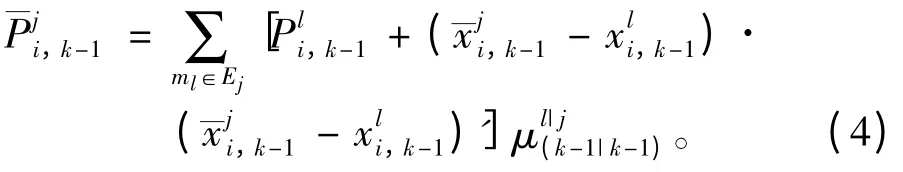
AGIMMUPF 算法的詳細步驟如下:

1)初始化，k=0

?mj∈M1，抽取符合先驗概率密度的N個粒子及其協方差。

2)交互運算

由于k 時刻使用的模型集合和k-1 時刻的模型有可能不同，對于新模型可以利用式(3)為其分配粒子，并利用式(4)確定協方差，而對于原有的舊模型則仍用文獻［10］中的交互步驟進行粒子的輸入交互。

3)UKF 濾波，k=1，2，…

?mj∈Mk，首先計算Sigma 點:

式中:na=nx+nv+nw，λ=α2(na+κ)-na，α 為正值的比例縮放因子，κ 為一個比例參數。并令:

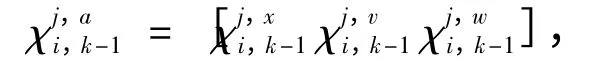
時間更新:

式中:

量測更新:

采樣粒子:

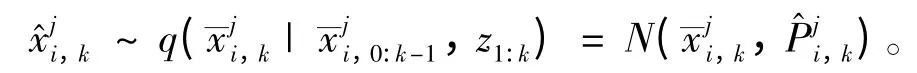
式中:N(·)表示高斯函數。

計算權重:

重采樣:

輸出融合結果:

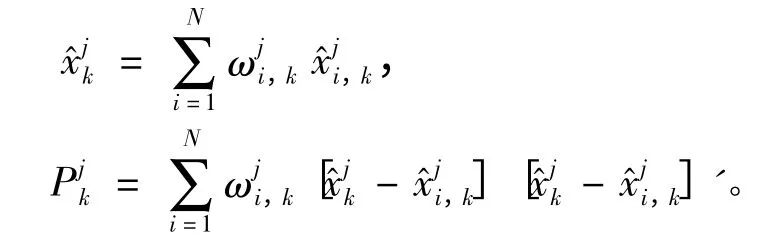
4)模型概率更新

模型mj∈Mk預測量測的均值和協方差分別為:

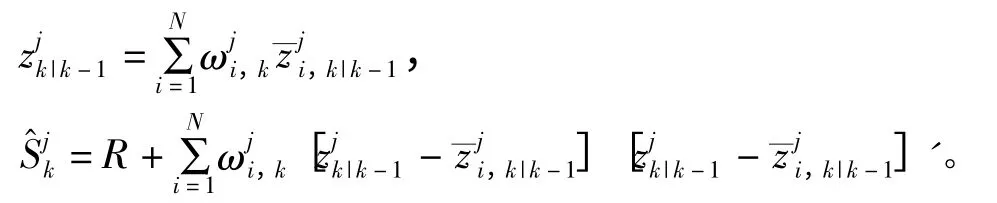
粒子的殘差為

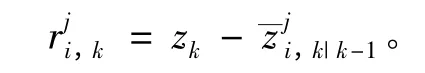
模型mj的似然函數

各模型概率更新:

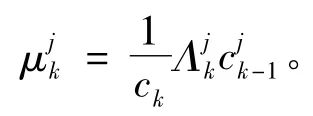
5)融合輸出

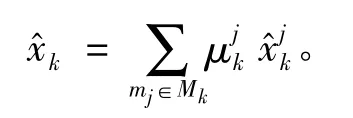
3 仿真結果與分析

為了比較本文提出的AGIMMUPF 算法和固定結構IMMUPF 算法的性能，考慮3 種固定結構IMMUPF算法:FGIMM3UPF，FGIMM5UPF 和FGIMM7UPF。這里FGIMMn(n=3，5，7)表示使用由n 個固定模型組成的模型集合的固定網格IMM 算法。

這里的仿真情況考慮對一個強機動目標的跟蹤。仿真中采用的機動模型為協同轉彎模型［11］。系統狀態方程和量測方程如下:

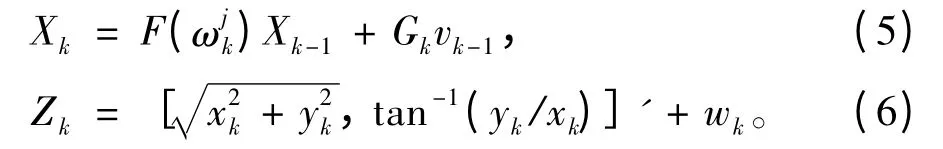
式中:

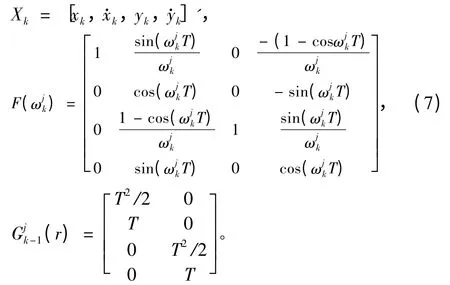
目標初始狀態為［50000，-72，55000，-46］′;機動想定為:在1 ～60 s，156 ～200 s，265 ～310 s，343 ～374 s，414 ～450 s 目標1 做勻速直線運動;在61 ～155 s，201 ～264，311 ～342 s，375 ～413 s，目標1 分別做了4 個180°轉彎，轉彎速率分別為1.87%，-2.8%，5.6%，-4.68°/s。

FGIMM3UPF 使用的固定網格為{-1.87°/s，0°/s，1.87°/s}，FGIMM5UPF 使用的固定網格為{-3.74°/s，-1.87°/s，0°/s，1.87°/s，3.74°/s}，FGIMM7UPF 使用的固定網格為{-5.6°/s，-3.74°/s，-1.87°/s，0°/s，1.87°/s，3.74°/s，5.6°/s}。AGIMMUPF 算法的初始網格為{-1.87°/s，0°/s，1.87°/s}。系統過程噪聲和量測噪聲均為零均值0，方差分別為Q=diag{［3，3］}和R=diag{［200，0.005］}的加性高斯白噪聲。采樣周期T=1 s。蒙特卡羅仿真次數為50 次。粒子數目為800。

圖1 和圖2 分別為AGIMMUPF，FGIMM3UPF，FGIMM5UPF 和FGIMM7UPF 算法對目標濾波的位置均方根誤差(RMSE)。表1 給出了4 種濾波算法對目標的濾波平均RMSE。平均RMSE 定義為［12］

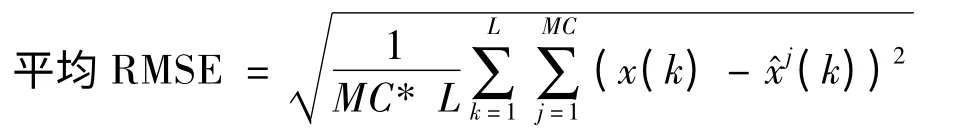
式中:MC 為仿真次數;L 為仿真長度;x(k)為真實值;為估計值。算法1 ～4 分別代表AGIMMUPF，FGIMM3UPF，FGIMM5UPF 和FGIMM7UPF。表2 為50 次Monte Carlo 各算法所用的時間。

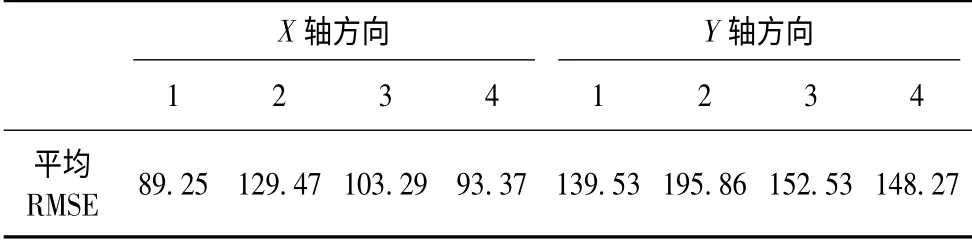
表1 4 種濾波算法的位置平均均方根誤差/mTab.1 The mean comparison of RMSE in position for different algorithms size/m

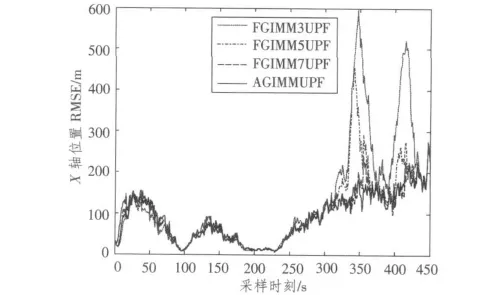
圖1 X 軸方向位置RMSE 曲線Fig.1 RMSE in position on X axis

從圖1 和圖2 可以看出，在對目標的跟蹤過程中，FGIMM3UPF 在第3、4 轉彎處(轉彎率分別為5.6°/s 和-4.68°/s)出現了非常大的誤差，這是由于這2 處的轉彎率已經大大超出FGIMM3UPF 所使用網格的覆蓋范圍;FGIMM5UPF 在上述2 處也出現了較大的誤差，因為FGIMM5UPF 使用網格的覆蓋范圍雖然比FGIMM3UPF 大1 倍，但相比于上述2 處的轉彎率仍有較大的差距;而 AGIMMUPF 和FGIMM7UPF 的性能明顯優于 FGIMM3UPF 和FGIMM5UPF。這是由于FGIMM7UPF 的模型集合完全覆蓋了目標的機動方式，而AGIMMUPF 通過自適應網格實現了模型集合自適應調整，也可以完全覆蓋目標的機動方式。從表1 可看出，AGIMMUPF 算法的性能稍優于FGIMM7UPF，這說明對于固定結構IMMUPF 而言，使用過多的模型會導致在當前時刻所使用的模型之間存在不一致，從而引起模型之間不必要的競爭，因此未必能保證跟蹤性能的提高。從表2還可看出，AGIMMUPF 計算量比FGIMM3UPF 高約12%，只有FGIMM7UPF 的40%。綜合上面分析可知，AGIMMUPF 可以提高IMMPF 算法的費效比。

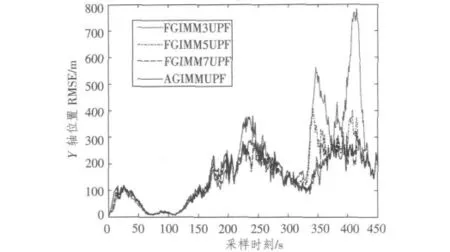
圖2 Y 軸方向位置RMSE 曲線Fig.2 RMSE in position on Y axis

表2 50 次Monte Carlo 仿真各算法所用時間Tab.2 Computation time of 50 Monte Carlo simulation used by the algorithms

4 結 語

本文將一種變結構多模型算法——自適應網格交互多模型(AGIMM)算法和UPF 算法相結合，提出了自適應網格交互多模型不敏粒子濾波算法(AGIMMUPF)。該算法通過自適應網格實現了模型自適應，從而以較小的模型集合覆蓋了目標大范圍的機動，并以此來克服固定結構IMMPF 存在的缺陷，同時各模型濾波算法采用不敏粒子濾波(UPF)，使重要性密度函數融合了最新量測信息，更好地逼近真實狀態的后驗概率分布。通過計算機仿真證明，提出的算法可以有效提高IMMPF 的費效比。

［1］LI X R，BAR-SHALOM Y.Multiple-model estimation with variable structure［J］.IEEE transactions on automatic control，1996，41(4):478-493.

［2］CAPPE O，GODSILL S J，et al.An overview of existing methods and recent advances in sequential Monte Carlo［J］.Proceedings of the IEEE，2007，95(5):899-924.

［3］BOERS Y，DRIESSEN J N.Interacting multiple model particle filter［J］.IEE Proceedings-Radar Sonar Navigation，2003，150(5):344-349.

［4］DRIESSEN H，BOERS Y.Efficient particle filter for jump Markov nonlinear systems［J］.IEE Proceedings-Radar Sonar Navigation，2005，152(5):323-326.

［5］MORELANDE M R，CHALLA S.Maneuvering target tracking in clutter using particle filters［J］.IEEE Transactions on Aerospace and Electronic Systems，2005，41(1):252-270.

［6］劉貴喜，等.改進的交互式多模型粒子濾波跟蹤算法［J］.電子與信息學報，2007，29(12):2810-2813.

LIU Gui-xi，et al.Tracking algorithms based on improved interacting multiple model particle filter［J］.Journal of Electronics ＆ Information Technology，2007，29(12):2810-2813.

［7］張俊根，等.IMM 迭代擴展卡爾曼粒子濾波跟蹤算法［J］.電子與信息學報，2010，32(5):1116-1120.

ZHANG Jun-gen，et al.IMM iterated extended Kalman particle filter based target tracking［J］.Journal of Electronics ＆ Information Technology，2010，32(5):1116-1120.

［8］FOO P H，et al.Combining the interacting multiple model method with particle filters for manoeuvring target tracking［J］.IET Radar Sonar Navig.，2011，5(3):234-255.

［9］黨玲，許江湖，王永斌.自適應網格交互多模型算法［J］.火力與指揮控制，2004，29(4):51-54.

DANG Ling，XU Jiang-hu，WANG Yong-bin.Adaptive grid interacting multiple model algorithm［J］.Fire Control and Command Control，2004，29(4):51-54.

［10］朱志宇.粒子濾波算法及其應用［M］.北京:科學出版社，2010.

［11］LI X R，et al.Design of an interacting multiple model algorithm for tracking in air traffic control systems.IEEE Transactions on Control Systems Technology，1993，1(3):186-194.

［12］胡士強，敬忠良.粒子濾波原理及其應用［M］.北京:科學出版社，2010.