CdnSn(1≤n≤12)團簇結構與電子性質的密度泛函理論研究

楚合營 劉朝霞 羅華平 張景川 胡蕓莎

(塔里木大學機械電氣化工程學院，新疆阿拉爾 843300)

Ⅱ－Ⅵ族半導體材料由于具有獨特的物理和化學性質，一直深受研究人員的關注［1－5］。例如ZnO、ZnS、CdS、CdSe等都是直接帶隙半導體，其能隙覆蓋了整個可見光范圍，因而是一類具有廣泛應用前景的光敏材料。隨Ⅱ－Ⅵ族半導體量子點實驗研究的不斷深入，Ⅱ－Ⅵ族半導體材料的理論研究也越來越受到科學家的重視，特別是對Ⅱ－Ⅵ族半導體團簇的理論研究［5－14］。與有機發光材料相比，CdS這種無機量子點不僅具有豐富的顏色，而且能夠承受多次的激發和光發射而不會分解，因此CdS這種無機量子點可以作為示蹤粒子或分子標簽在生物化學、分子生物學、細胞生物學、基因組學、蛋白質組學、藥物篩選和生物大分子相互作用等研究中扮演重要角色。對CdnSn半導體團簇進行研究，有助于人們對CdS量子點光學以及電子性質的研究。但是，由于團簇的電子性質對團簇的結構比較敏感，同時隨著原子個數的增加，團簇的初始結構成指數增長，計算工作量也越來越大，因此給較大CdnSn半導體團簇的理論研究帶來了極大的挑戰。根據文獻報道，相對其它Ⅱ－Ⅵ族半導體團簇而言，對CdnSn半導體團簇的研究文獻報道還比較少。因此，進一步開展對CdnSn半導體團簇的研究對于認識CdS量子點以及CdnSn半導體團簇的生長方式和電子性質都是十分必要的。利用Dmol3模擬軟件包對CdnSn(1≤n≤12)團簇的幾何構型進行優化，并對其能量、頻率以及電子性質進行了模擬分析。

1 計算方法

在Dmol3軟件包上，采用密度泛函理論(DFT)下的廣義梯度近似(GGA)對CdnSn(1≤n≤12)團簇的幾何結構進行優化，并對其電子性質進行計算機模擬。在廣義梯度近似下，選用Perdew－Wang(PW91)交換關聯泛函。為了獲取最精確的計算數據，所有的計算均是在Fine網格下完成的，采用帶極化的雙數值原子基組(DNP)進行全電子計算，自洽過程以體系的能量和電荷密度分布是否收斂為依據，精度均優于10－5a.u.，梯度和位移的收斂精度優于2.0 ×10－3a.u./nm 和 5.0 ×10－3nm，能量的收斂精度優于1.0 ×10－5a.u.。CdnSn 半導體團簇的初始構型，在借鑒文獻［11－14］報道的Ⅱ－Ⅵ族半導體團簇結構的基礎上，進行了進一步的擴充。

2 結果與分析

2.1 團簇結構分析

由于團簇的結構決定了團簇的物理和化學性質，所以在團簇研究中團簇的結構就成為團簇研究中的一項主要研究內容。在對CdnSn(1≤n≤12)半導體團簇的初始構型進行幾何結構優化的同時對團簇的振動頻率進行了計算，把總能量最低且最小振動頻率為正值的結構確定為團簇的最低能量結構。團簇的能量越低，團簇也就越穩定。圖1給出了CdnSn(1≤n≤12)半導體團簇的最低能量結構。表1列出了CdnSn(1≤n≤12)半導體團簇的最低能量結構下的對稱性(Symmetry)，Cd－S鍵長(R)，能隙(Egap)，平均結合能 Eb=(nECd+nES－ECdnSn)/2n，Cd和S的Mulliken原子電荷數(Q)，最低振動頻率(ωmin)。

圖1 CdnSn(1≤n≤12)半導體團簇的最低能量結構(黑色小球代表硫原子，灰色小球代表鎘原子)

如圖1所示，n=1時團簇的結構最為簡單，計算結果顯示CdS團簇的對稱性為Cinfv，Cd－S鍵長為2.36埃，平均結合能和能隙分別為1.010 eV·atom－1和0.233eV，與文獻［11］給出 Cd － S 鍵長的計算結果相一致，并且接近于實驗值(2.52埃)，這說明選取的計算參數是準確的，而且在Fine網格下對團簇結構及電子性質進行模擬也是必要的。當n=2時，計算結果顯示Cd2S2的最低能量結構是平面結構，團簇的對稱性為D2h，鍵長為2.50埃，能隙為1.218 eV。當n=3時，Cd3S3團簇的最低能量結構仍然是平面結構，團簇的對稱性為D3h，鍵長為2.43埃，能隙為2.542 eV。從圖1 CdnSn團簇的最低能量結構可以看出，Cd2S2和Cd3S3團簇的最低能量結構可以看成是組成4≤n硫化鎘團簇最低能量結構的兩個亞單元。

表1 CdnSn(1≤n≤12)團簇最低能量結構下的對稱性(Symmetry)，Cd－S鍵長(R)，能隙(Egap)，平均結合能(Eb)，Cd和S的Mulliken原子電荷(Q)，最低振動頻率(ωmin)

當n=4時，CdnSn團簇的最低能量結構不再是平面結構，而是三維籠狀結構，如圖1所示。Cd4S4可以看成是由6個Cd2S2單元相互連接而成的多面體，Cd4S4的對稱性為Td、鍵長為2.61埃、能隙為2.154eV、平均結合能為2.222 eV·atom－1。當n=5時，Cd5S5團簇的最低能量結構可以看成是由4個Cd2S2和兩個畸變的Cd3S3連接而成。當n=6時，團簇Cd6S6的最低能量結構可以看成是由6個Cd2S2和兩個Cd3S3亞單元連接而成。當n=7時，從圖1可以看出Cd7S7團簇的最低能量結構可以看成是由6個Cd2S2和3個Cd3S3亞單元構成的一個完美的籠。當n=8時，Cd8S8可以看成是由6個Cd2S2和4個Cd3S3亞單元相互連接而成。當n=9時，團簇Cd9S9可以看成是由Cd2S2和Cd3S3兩個亞單元組成的籠型結構。隨著團簇原子個數的增加，團簇的初始結構迅速的增多，為了減少計算工作量，在構建團簇初始結構時盡量多的使用Cd2S2和Cd3S3團簇的最低能量結構作為構建團簇的亞單元，結果顯示這種嘗試是非常有效的。

圖2 CdnSn(1≤n≤12)團簇的總能量二階有限差分△2E(n)=E(n－1)+E(n+1)－2E(n)隨n的變化關系

當n=10時，團簇Cd10S10的能量最低能量結構可以看成是由6個Cd2S2和6個Cd3S3團簇亞單元構建成的籠狀團簇，顯然隨著團簇原子個數的增加，團簇的結構越來越復雜。當n=11時，Cd11S11可以看成是由6個Cd2S2和7個Cd3S3團簇基元構建成的。當n=12時，Cd12S12則可以看成是由6個Cd2S2和8個Cd3S3團簇的亞單元組成的球狀結構，從而使由Cd2S2和Cd3S3兩個亞單元構成CdnSn團簇最低能量結構達到了一個極致。從表1給出的CdnSn(1≤n≤12)團簇最低能量結構下的對稱性(Symmetry)，Cd－S鍵長(R)，能隙(Egap)，平均結合能(Eb)，Cd和S的Mulliken原子電荷(Q)，最低振動頻率(ωmin)不難看出，隨著n的增加團簇的性質逐漸向CdS晶體的性質過渡。這說明圖1給出的CdnSn(1≤n≤12)團簇的生長規律是合理的。

綜上所述，當n≤3時，團簇的最低能量結構為平面結構;當4≤n≤12時，團簇的最低能量結構為三維籠狀結構。值得注意的是4≤n≤12團簇的最低能量結構可以看成是由團簇Cd2S2或Cd3S3兩個亞單元構成。這和文獻［11－14］報道的 ZniSi，CdnSen，CdnSn團簇的最低能量結構相似。從圖1 CdnSn(4≤n≤12)團簇的最低能量結構不難看出，鎘和硫每個原子的配位數都為3，而鎘原子與硫原子的最外層電子排布分別為4d105s2和3s23p4，因此CdnSn(4≤n≤12)團簇的最低能量結構里的鎘原子與硫原子最外層電子容易形成SP2雜化，從而降低了硫化鎘團簇的總能量。

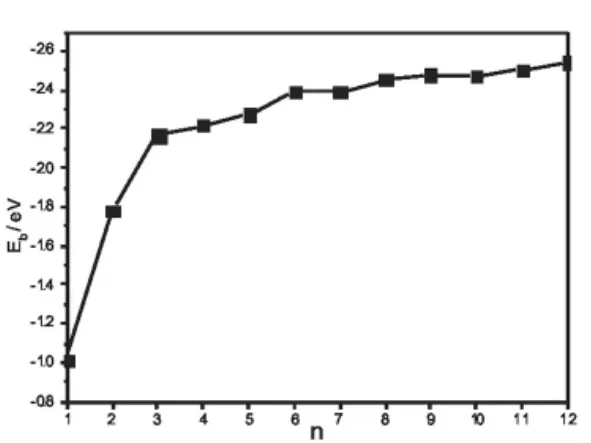
圖3 CdnSn(1≤n≤12)最低能量結構團簇的平均結合能Eb=(nECd+nES－ECdnSn)/2n隨n的變化曲線

2.2 電子性質分析

為了研究團簇的相對穩定性，圖2給出了硫化鎘團簇的總能量二階有限差分(△2E(n)=E(n－1)+E(n+1)－2E(n))隨n的變化關系。眾所周知，團簇的總能量二階有限差分是反映團簇的相對穩定性比較靈敏的一個物理量。從圖2可以看出，在n=3、6和9處出現了極大值，這表明n=3、6和9為半導體團簇CdnSn(1≤n≤12)的幻數。團簇Cd3S3，Cd6S6和Cd9S9在實驗制備時的豐度會相對比較大。

圖4 CdnSn(1≤n≤12)半導體團簇的能隙EGap隨n的變化規律曲線

圖3給出了半導體團簇CdnSn(1≤n≤12)最低能量結構的平均結合能Eb隨n的變化曲線。團簇的平均結合能Eb是也反映團簇相對穩定性的一個重要物理量。從圖3不難看出，隨著團簇尺寸的增加，團簇最穩定結構的平均結合能逐漸增大，這說明團簇在生長過程中能繼續獲得能量。在n=3、6和9處出現了極大值，這進一步表明團簇Cd3S3、Cd6S6和Cd9S9比它們鄰近的團簇更穩定。這也從另一個方面說明半導體團簇CdnSn(1≤n≤12)的幻數為n=3、6 和9。

為了更進一步研究團簇的相對穩定性，圖4給出了團簇的最高已占據軌道(HOMO)與最低未占據軌道(LUMO)之間的能隙Egap隨團簇尺寸的變化規律。能隙反映了電子從占據軌道向未占據軌道發生躍遷的能力，在一定程度上反映了團簇參與化學反應的能力。從圖4不難看出，與近鄰的團簇相比，團簇 Cd3S3、Cd6S6和 Cd9S9的能隙較大，這表示Cd3S3、Cd6S6和Cd9S9團簇的化學活性比較弱，也就是說團簇Cd3S3、Cd6S6和Cd9S9相對穩定一些。這與前面團簇的總能量二階有限差分以及團簇最低能量結構下的平均結合能的分析結果相一致。表1給出的Cd3S3、Cd6S6和 Cd9S9團簇的能隙分別為2.542eV、2.407eV和2.517eV，比其相鄰的團簇的能隙都要大一些兒。這更進一步說明n=3、6和9為CdnSn(1≤n≤12)半導體團簇的幻數。同時，顯示Cd3S3、Cd6S6和Cd9S9可能是構成CdS量子點的重要組成部分，這對于研究小于1nm的CdS量子點的結構以及電子性質具有重要的理論價值。更值得一提的是模擬結果顯示硫化鎘團簇的能隙Egap與平均結合能Eb隨團簇尺寸n的變化規律完全一致，這說明圖1給出的硫化鎘團簇的最低能量結構是合理的，表1給出的模擬數據也是準確可靠的。

3 結論

采用基于密度泛函理論的廣義梯度近似對CdnSn(1≤n≤12)半導體團簇的幾何結構進行了優化，并對其總能量、振動頻率以及電子性質進行了模擬。結果顯示，當n≤3時，團簇的最低能量結構為平面結構;當4≤n≤12時，團簇的最低能量結構為三維籠狀結構。4≤n≤12團簇的最低能量結構可以看成是由團簇Cd2S2或Cd3S3兩個亞單元構成。CdnSn(1≤n≤12)半導體團簇的總能量二階有限差分△2E(n)，平均結合能Eb以及能隙Egap都表明n=3、6和9為團簇的幻數。CdnSn(4≤n≤12)團簇的最低能量結構里的鎘原子與硫原子最外層電子形成SP2雜化，是造成團簇能量較低的主要原因。

［1］Ma Hong，Ma Guo－Hong，Wang Wen －Jun，et al.Size－dependent optical properties and carriers dynamics in CdS，ZnS quantum dots［J］.Chin.Phys.B，2008，17:1280.

［2］Wu Si－Xin，Chu He－Ying，Xu Hong－Tao，et al.Oscillation of absorption bands of Zn1－xMnxS clusters:an experimental and theoretical study［J］.Nanotechnology，2008，19:055703.

［3］Antonietta Tomasulo，Mushti V.Ramakrishna.Quantum confinement effects in Smiconductor clusters.II［J］.J.Chem.Phy.，1996，105:3612－3626.

［4］Claudia Troparevsky M，Leeor Kronik，James R.Chelikowsky.Optical properties of CdS quantum dots［J］.Phys.Rev.B，2001，65:033311.

［5］Jan － Ole Joswig，Michael Springborg，Gotthard Sifert.Structural Electronic Properties of Cadmium Sulfide Clusters［J］.J.Phys.Chem.B，2000，104:2617 －2622.

［6］Trave A，Buda F，Slloni A.CdS Microclusters in Sodalite Frameworks of Different Composition A Density Functional Study［J］.J.Phys.Chem.B，1998，102:1522－1527.

［7］Claudia Troparevsky M，James R.Chelikowsky.Structural and electronic properties of CdS and CdSe clusters［J］.J.Chem.Phys.，2001，114:943 －949.

［8］Claudia Troparevsky M，Leeor Kronik，James R.Chelikowsky.Ab initio absorption spectra of CdSe clusters［J］.J.Chem.Phys.，2004，119:2284 －2287.

［9］李春霞，黨隨虎，張可言，等.應用第一性原理對CdSe和HgTe團簇結構和電子性質的研究［J］.原子與分子物理學報，2008，25:542.

［10］李春霞.中小尺寸CdS和CdTe團簇結構與電子性質的第一性原理研究［J］.原子與分子物理學報，2007，24:1060.

［11］Chu H －Y，Liu Z－X，Qiu Guo－Li，et al.Firstprinciples study of structures and electronic properties of cadmium sulfide clusters［J］.Chin.Phys.B，2008，17:2478－2483.

［12］CdnSen(1≤n≤12)團簇結構與電子性質的第一性原理研究，劉朝霞，楚合營，胡蕓莎，等.原子與分子物理學報，2011，28，0048.

［13］Jon M.Matxain，JoSph E.Fowler，and Jesus M.Ugalde.Small clusters of II－VI materials ZniSi(i=1－9)［J］.Phys.Rev.A，2000，61:053201.

［14］Eleonora Spano，Said Hamad，C.Richard A.Catlow.Computational Evidence of Bubble ZnS Clusters J.Phys.Chem.B，2003，107:10337－10340.