關聯運輸調度問題的蟻群算法

廣東工業大學自動化學院 湯雅連 蔡延光 趙學才

1.引言

車輛路徑問題（Vehicle Routing Problem，VRP）最早由Dantzig，Fulkerson和Johnson于1959年提出。VRP問題是一個組合優化問題，而關聯物流運輸調度問題（Related Vehicle Routing Problem，RVRP）也是車輛路徑問題的延伸，所以也屬于NP-hard問題。近年來，遺傳算法、模擬退火算法、粒子群算法、蟻群算法等現代啟發式算法為VRP的求解提供了極大的便利。

蟻群算法[1-3]是解決VRP問題的一種有效的元啟發式方法，其中改進的螞蟻系統[4]有帶精英策略的螞蟻系統（Ant System with elitist strategy，ASelite）、基于優化排序螞蟻系統（Rank-Based Version of Ant System，SArank）、蟻群系統（Ant Colony System，ACS）、最大-最小螞蟻系統（Max-Min Ant System，MMAS）以及最優-最差螞蟻系統（Best-Worst Ant System，BWAS）。蟻群算法[5]的提出，為解決路徑規劃問題提供了新的思路和解決方法，但是傳統蟻群算法與其他進化算法同樣存在易于陷入局部最優、早熟收斂等缺陷，為了提高蟻群算法的全局搜索能力，提高其收斂速度，該文提出了保留每代最優解，并自適應改變信息素揮發因子，從而克服傳統蟻群算法的不足。

2.問題描述及數學模型的建立

2.1 問題描述

關聯物流運輸調度問題也是車輛路徑問題的延伸，所以具有相似性。問題可以簡單描述為，假設給定車場信息以及客戶信息（位置和貨物需求量等），貨物之間的關聯系數，車輛信息（載重約束、里程約束和容量約束等），要求合理安排車輛和運輸路線，在滿足所有客戶需求的前提下，使配送成本最低。

2.2 數學模型

第i個客戶的貨運量為gi（i=1，2，…，l），需要從車場將貨物運到客戶手中，有車場派出載重量為q的貨車若干，已知gi＜q。

預先對需要車輛數進行估計。可以按照式（1）確定車輛數：

式中，[ ]表示不大于括號內數字的最大整數； 0＜α＜ 1，是對裝車（或卸車）的復雜程度及約束多少的估計。

以cij表示為從點i到點 j的運輸成本（距離、費用、時間等），cij=cji。假設客戶i， j之間的距離為：dij。車場編號為0，客戶為：i（i=1，2，…，l）。關聯系數為：r，rij表示點i處的貨物與點j處貨物的關聯系數。目標為使車輛的總運輸距離最短。

定義變量如下：

目標函數式（4）表示總運輸距離最短，以cij表示從點i到點j的運輸成本并用客戶i與 j之間的距離dij作為取值。（5）為車輛行駛距離約束，其中dijk表示車輛k行駛了客戶i到 j的路程，n是車輛k服務的客戶數目，最大為N。（6）和（7）表示兩個變量之間的關系。（8）表示車輛服務客戶i后直接行駛到j為其服務。（9）表示每個客戶只能由1輛車來服務且每個客戶都能得到服務。（10）表示每輛車所運送的貨物重量不能超過車輛載重量的限制。（11）表示保證每輛車的客戶總數小于等于總客戶數目。（12）為關聯系數rij的取值約束，當i與j的貨物不可用同輛車配送時，應選擇其他客戶的貨物。

3.一種自適應蟻群算法

3.1 基本蟻群算法

設m為螞蟻數量，dij(i，j=1，2，...，n)表示i與j之間的距離， τij(t)表示t時刻在ij連線上殘留的信息素強度。初始時刻，各路徑上信息量相等，設τij(0)=C（C為常數）。螞蟻 k(k =1，2，...， m)在運動過程中，根據各條路徑上信息量決定轉移方向，Pijk表示t時刻螞蟻k由位置i轉移到j的概率，如式（13）所示。

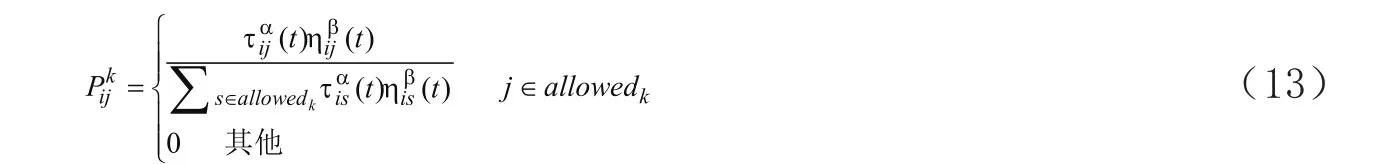
其中 allowedk為螞蟻k下一步可選擇的城市。 ηijβ為能見度因數，常取ηij(t)=1/dij。α和β分別反映了螞蟻在運動過程中所積累的信息和啟發信息在螞蟻選擇路徑中的相對重要性，α為信息啟發式因子，β為期望啟發式因子。

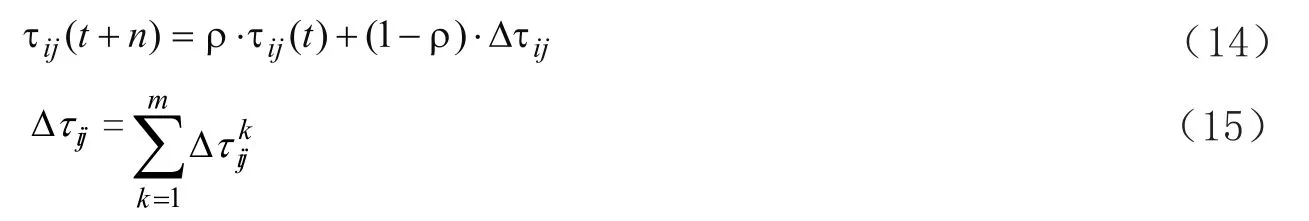
過多殘留信息素會引起殘留信息素覆蓋啟發信息，所以在每只螞蟻走完一步或者完成對所有城市的遍歷之后，要對殘留信息進行更新處理。t+n時刻在路徑(i，j)上的信息量可按式（14）和（15）做調整。

ρ為信息素揮發因子， ρ∈ （0，1）， Δτij(t)表示本次循環中信息素增量。表示第k只螞蟻在本次循環中留下的信息素，計算方法可以根據計算模型而定，本文采用最常用的蟻周模型，如式（16）所示。

式中Q表示信息素強度，會影響算法的收斂速度，過大會導致局部收斂，過小會影響收斂速度。Lk表示在本次循環中所走路徑的長度。

3.2 構造狀態轉移規則

本文采用將確定性選擇組合和隨機性選擇相結合的策略，為了縮短最好和最差路徑上的信息量差距，適當加大隨機選擇概率，對解空間進行更完全搜索，從而克服傳統蟻群算法缺陷。按照下式確定螞蟻k由i轉移到j的狀態轉移概率。

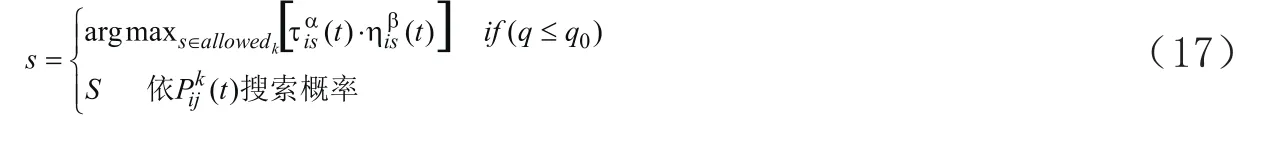
q是[0，1]內的隨機數，q0是一個 參 數 ， q0∈ [0，1]， 一 般 取0.85～0.90。螞蟻在選擇下一客戶時，根據先驗知識，如式（17）所示來選擇最好的邊，否則按式（13）來選擇一條邊，將求得的各個節點的轉移概率進行累加，再與產生的隨機數相比較，直到滿足要求，螞蟻可轉移到下一節點。

3.3 信息素更新

3.3.1 保留最優解

在每次循環結束后，保留最優解。

3.3.2 自適應改變ρ

通過減小ρ雖然可以提高算法的全局搜索能力，但也會使收斂速度降低，因此需要自適應改變ρ。ρ的初始值 ρ( t0)=1；當算法求得最優值在N次循環中無明顯改進時，ρ如式（18）所示。其中ρmin可以防止ρ因過小而降低算法收斂速度。

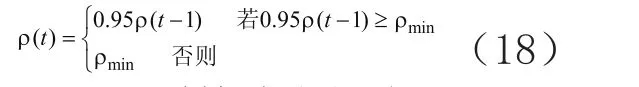
3.4 蟻群算法求解流程

Step1：初始化參數，包括Nc，螞蟻總數m，信息啟發式因子α，期望啟發式因子β，信息素揮發因子 ρ( t0)，信息素強度Q；

Step2：將螞蟻隨機置于節點；

Step3：螞蟻根據轉移概率選擇下一節點，判斷是否超過載重限制，若沒有，加入禁忌表中；否則，選擇另一個節點進行判斷；

Step4：若沒有滿足條件的節點，則將車場編號加入禁忌表中，表示完成子路徑的搜索。重新將載重置0，執行Step3；

Step5：直到所有螞蟻都訪問了所有節點，每條螞蟻將得到若干條以車場為起終點的回路，回路就是一輛車的路徑軌跡；

Step6：計算每條回路的路徑長度，得出局部最優解；

Step7：進行信息素全局更新；

Step8：若滿足終止條件，達到最大迭代次數，則結束，否則，轉Step2。

4.仿真分析

某供應處有1個車場，需給32個客戶送貨，客戶信息表如表1所示。每輛車最大載重為20噸，每輛車最大配送里程為100km。貨物與貨物之間的關聯系數由Matlab7.1隨機生成。

本文中的實驗是在Intel(R)Core?i3 CPU2.53GHz、內存2.0G的PC機上采用Microsoft Visual C++6.0編程以及Matlab7.1輔助編程實現。利用VC++6.0進行編程，蟻群算法中參數設置：蟻群規模m為100，最大迭代次數Nc=200，α =1，β=2， ，q0=0. 88，Q=100。運行程序30次，得到該算法求解本算例的最優結果，最短運輸距離為268.24千米，如表2所示，配送示意圖如圖1所示。

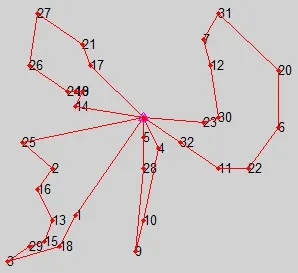
圖1 配送路徑示意圖

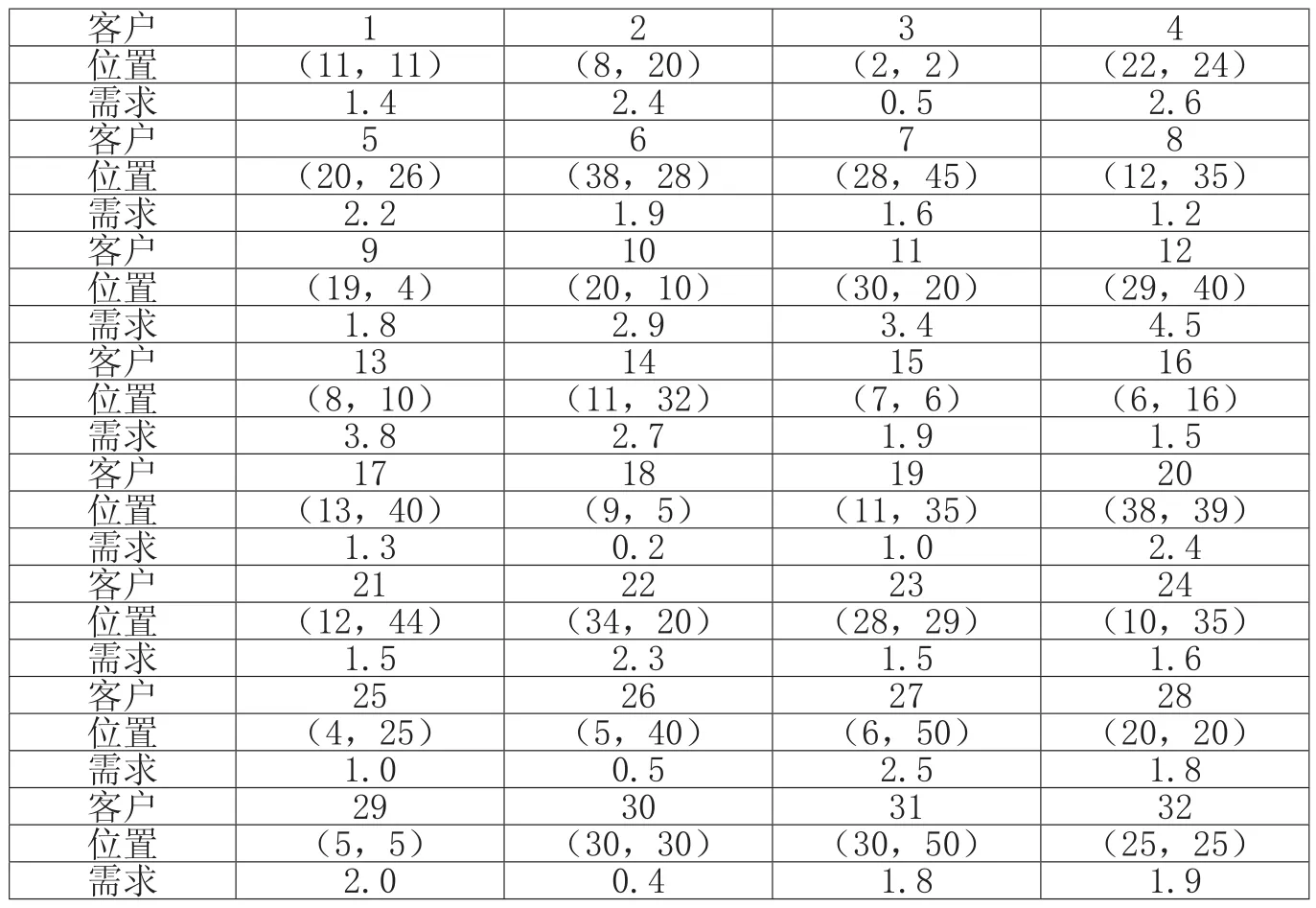
表1 客戶信息表

表2 各配送車輛的配送數據

5.結束語

該文對傳統的蟻群算法進行改進，通過自適應改變信息量的揮發因子，既保證了收斂速度，又提高了算法的全局搜索能力。運用改進的蟻群算法對建立的單車場單車型無時間窗約束的關聯物流運輸調度模型進行求解，實驗結果證明了算法的可行性和有效性。