自主創新績效評價體系與測度方法*——以鄭州市為例

河南農業大學 信息與管理科學學院 溫 建 雷麗娟 汪松玉

衡量自主創新在經濟發展中的績效，對于認清區域自主創新現狀、建設創新型國家具有十分重要的意義。評價區域自主創新的績效，對于動態掌握自主創新的進展和成果、發現創新系統存在的問題和原因，以便采取有針對性的措施、優化創新資源的結構和配置、調整創新的產出目標和方向、進一步提高創新系統的效率，對區域自主創新網絡建設和政策制定具有重要指導意義。作為推動自主創新效率的主要行政層次，城市具有較強的資源集聚優勢，因此，本研究從城市視角研究自主創新效率具有重要的戰略意義。如何科學地評價鄭州市的自主創新效率和自主創新能力，解決自主創新環節中存在的主要問題，是鄭州實施“三化兩型城市”戰略，獲取自主創新優勢，增強核心競爭力所面臨的關鍵任務。

為從自主創新投入產出效率方面來測度城市的自主創新效率，探討鄭州市自主創新效率的水平、特征以及主要影響因素，并據此提出有針對性的策略，以提升鄭州市自主創新效率，促進鄭州市經濟的持續發展。本文，筆者提出鄭州市自主創新績效的理論初始評價指標，采用粗糙集等方法對理論評價指標進行了多重的實證篩選，構建包括自主創新投入能力3個指標和自主創新產出能力4個評價指標的“創新型鄭州”自主創新績效評價體系。采用DEA 方法的非阿基米德無窮小CCR 模型和超效率的DEA 模型，結合自主創新的投入和產出的特點，根據2001—2008年鄭州市的指標數據，進而對鄭州自主創新效率進行較為合理的測評。

一、鄭州市科技自主創新現狀

鄭州市是河南省的省會城市，是國內重要的經濟大市，經濟發展水平和創新能力在中西部地區處于第一方陣。自主創新體系建設初具規模。2008年，鄭州市被列為“中國城市綜合創新實力50強”。2009年，榮獲國家知識產權示范城市稱號，進入國家“十城萬盞”試點城市行列，在連續四次獲得國家科技進步先進城市稱號基礎上，進入國家科技進步示范城市行列。2010年，鄭州市躋身于全國僅有的16個創新城市試點。

二、基于粗糙集的評價指標遴選

本文數據源于《河南科技統計年鑒》（2001—2009年）。參照國家統計局從技術創新能力角度提出的企業自主創新能力評價指標體系，及相關文獻，依據指標選取的系統性、科學性、客觀性、可比性及可操作性等原則，從自主創新投入能力、自主創新產出能力兩個方面，構建鄭州市自主創新績效評價初始指標體系。

1.鄭州市自主創新績效的初始評價體系。在創新績效評價中，我們認為，投入研發的人員和經費投入是主要投入，其產出的主要成果以科技論文和發明專利，高科技產品為代表。初始的創新績效評價體系如表1所示。

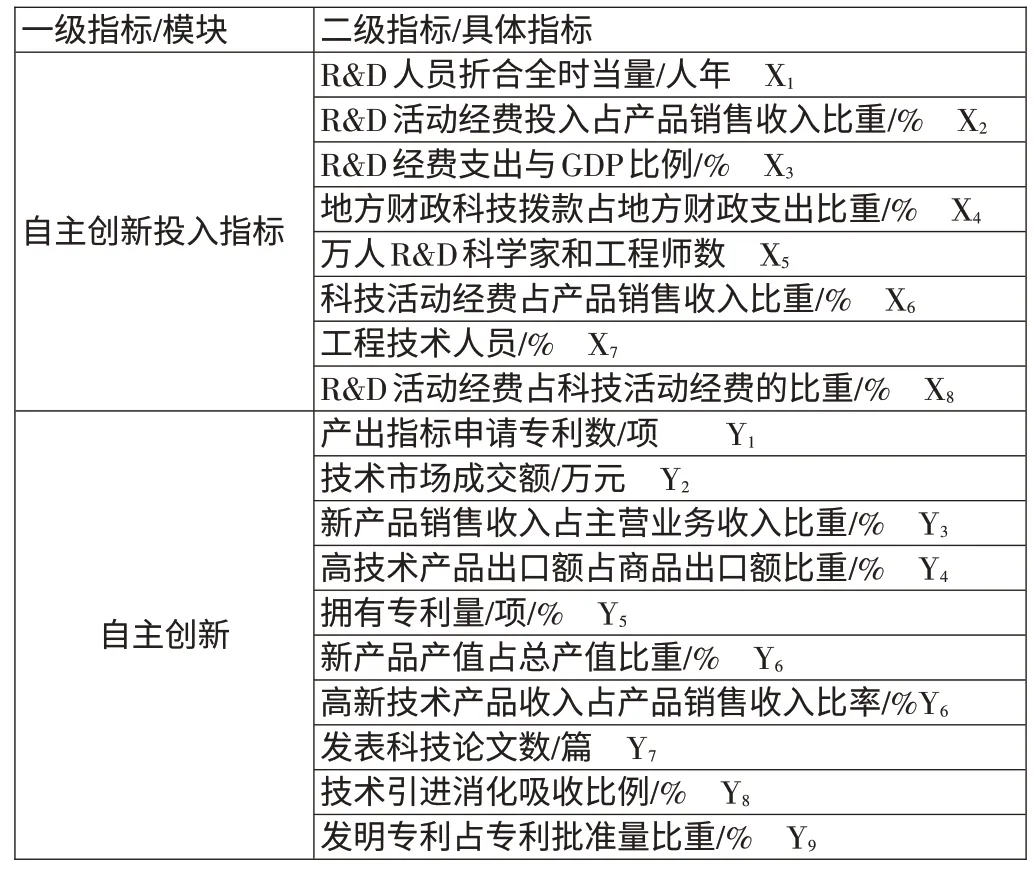
表1 鄭州市自主創新績效評價的初始體系

2.基于粗糙集的自主創新投入產出評價指標篩選。

步驟1，連續屬性離散化。由于粗糙集理論只能對數據庫中的離散屬性進行處理，在運用屬性約簡算法之前，需先將連續屬性離散成有限個語義符號。常用的離散化方法包括等距離法、等頻率法、最小信息熵法、層次聚類法、遺傳算法及SOM 網絡法等。筆者采用等頻率法對指標數據進行離散，中間過程略去。

步驟2，刪除重復對象。以投入指標為例說明約簡方法。由差別矩陣定義可知，矩陣中屬性組合數為1的屬性均為決策表的核屬性（可能為空）。經差別矩陣運算，得核屬性，建立相應的析取表達式，將析取表達式進行合取運算，最終得到析取范式L=（X1∧X2∧X3）∨（X1∧X3∧X7），根據專家意見，選取X1，X2，X3作為自主創新投入指標。

步驟3，其他指標約簡結果。重復上述步驟，同理可得其他指標約簡結果，結果見表2。

表2 優化后的鄭州市自主創新績效評價體系

通過對已有的評價指標的屬性簡約，得到優化后的鄭州市自主創新績效評價體系，該體系消除了以往研究體系中存在的信息重疊量大的問題，使得評價指標更加科學、合理。以下對于鄭州市自主創新績效的實證研究就是在此優化后的指標體系之上進行的，因此，所得出的結論具有更加客觀、科學的特點，從根據面板歷史數據，更能反映鄭州創新績效的實際水平。

三、基于超效率數據包絡的鄭州市自主創新績效評價

1.數據包絡方法的基本原理。DEA（Charnes、Cooper 和Rhodes；Banker、Charnes和Cooper）是一種數據驅使（data-driven）的非參數方法，依靠投入產出的數據挖掘出兩大信息：技術前沿和相對于參照技術的效率評價（非參數方法的最大優點是不需要設定生產者最優行為目標，諸如成本最小化、利潤最大化等，而且也不需要對生產函數的形式作特殊假定）。DEA 模型一般衡量評價對象的“規模有效”與“技術有效”，所謂技術有效是指“生產”處于最理想的狀態，相對于現有的輸入量可以獲得最大的輸出量，而規模有效就是“生產”處于規模效益不變的階段。

2.鄭州市自主創新績效評價的實證分析。從整體來看（圖1），鄭州市自主創新的技術效率呈現先降低后上升再降低的不規則變化，從2000年開始逐年上升，在2005年后又開始有下降的趨勢；規模效率與技術效率類似，但規模效率和技術效率在2001—2003年階段間的變化剛好相反，前者為正U型，后者為倒U型。

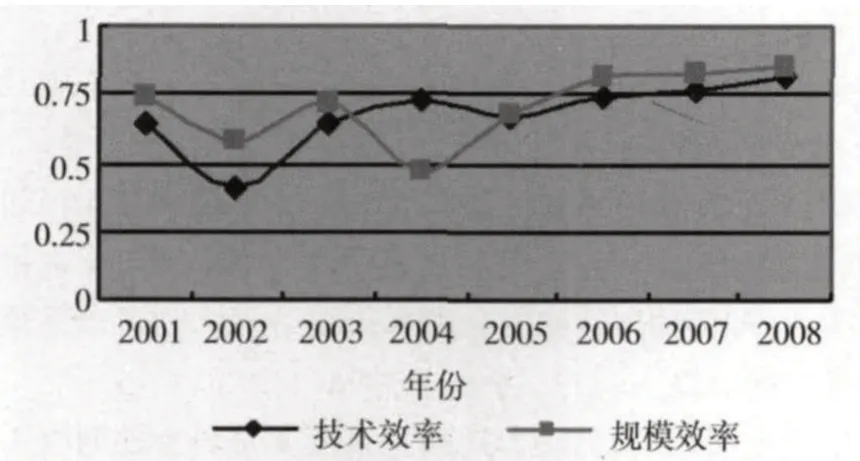
圖1 鄭州市自主創新績效歷年“有效”效率

從結果來看，鄭州市自主創新的技術效率和規模效率的變動整體基本上均是保持了先降低，再提高，然后增勢趨緩的一個發展趨勢，但技術效率和規模效率的變動并不一致，這充分表明鄭州市自主創新效率并非穩步提高。但總體來講，基于超效率的數據包絡分析結果（圖2），鄭州自主創新績效還是有一定程度的提升。定量分析的結果如下：（1）基于數據包絡分析方法的CCR 模型，2001—2004年的自主創新相對弱有效，2001—2004年相對有效?；诔实腄EA模型，鄭州市的得分逐年提升，表明鄭州市的自主創新能力穩步提升。（2）從分析結果看，單純從產出值或投入值來看，某些處于絕對優勢的年份，在將產出與所做的投入進行對比的情況下相對效率可能偏低，例如2005年。（3）用DEA模型評價自主創新效率的絕對值會隨著投入產出指標選取的變動發生相應的變化，而對于處于效率前沿面上的年份，即效率最好的年份的排序基本沒有多大改變：效率最差的年份的排序也基本維持不變；而對處于中間的年份，尤其是效率值比較接近的，自主創新相對效率的排序就可能發生很大改變。

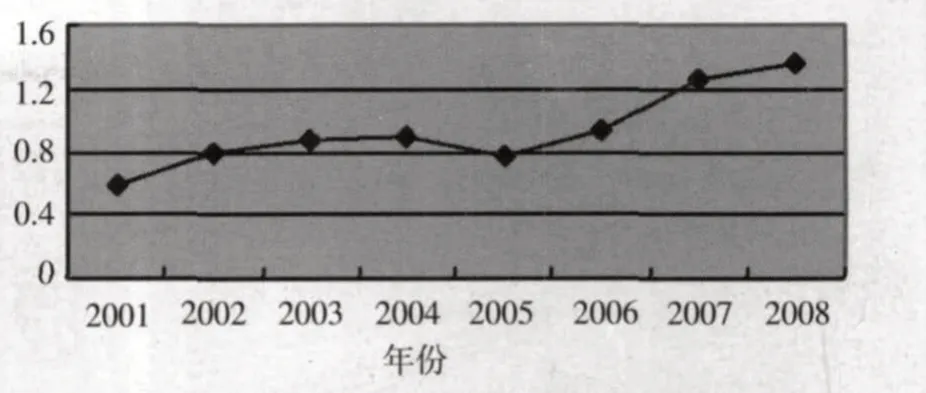
圖2 鄭州自主創新的技術超效率

3.鄭州市自主創新效率結果的分析。為進一步對鄭州市自主創新績效的年度差異進行探討，首先采用熵值來對各年份的R&D經費投入強度的差距進行計算。在物理學中，熵代表物質系統狀態的紊亂程度，系統越紊亂，熵值越大。根據公式：其中，Pi為各年份R&D 經費投入占GDP 的比重。從圖3可知，2001年以來，鄭州市科技投入的熵值呈直線上升趨勢。

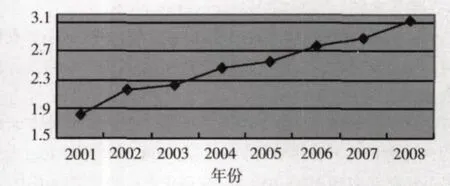
圖3 2001—2008年熵值的變化情況

從結果可以看出，R&D投入效率與各項指標之間均表現出正相關的關系。從超效率（技術效率）的結果來看，高投入強度和高效率并沒有產生有效的必然性，當投入強度從“低”到“中低”時技術效率一般達到第一個峰值，這說明從效率的角度出發，中低強度的投入是比較合適的。當投入強度繼續增加時，技術效率并沒有明顯的提高，而是呈現近似正弦三角函數的形狀，呈現非標準U 型的特征。從趨勢上看，似乎隨著投入強度的增大，表現出效率略有降低的趨勢。而且，最高投入強度和低投入強度的年份對比來看，二者的效率相差并不大。投入規模并沒有顯著影響R&D投入效率的高低。同時也可以發現，規模最大的年份技術效率并沒有同時位居前列，小規模的年份的效率并不低。

四、提升鄭州市科技自主創新效率的建議

鄭州市提升科技自主創新可以在如下幾個方面做好文章：建立宏觀調控管理體系，形成自主創新合力，加大全社會多元化投入，為創新體系建設提供資金保障，深化科技體制改革，建設創新型人才隊伍，為自主創新提供寬松的軟環境；創新管理，優化提升科技資源配置效能，激勵創新，培育創新文化。