中國月度嬰兒出生率預測

河南大學 數學與信息科學學院 王文靜

針對中國現階段老齡化趨勢不斷增加，筆者認為，有必要分析一下中國目前嬰兒出生率的狀況，選擇了《應用時間序列分析》課本上的某城市月度嬰兒出生率數據，經過用軟件對這些數據分析發現，分析結果符合中國現在的情況，即我國從過去的實行計劃生育政策鼓勵一個家庭要一個孩子，到現在的準許部分家庭要兩個孩子，從政策的放寬可以發現我國的月度嬰兒出生率在不斷地增加。根據這些數據對中國月度嬰兒出生率確定一個模型，可以預測未來中國嬰兒的出生情況。運用時間序列知識來解決實際中的問題，從某城市月度嬰兒出生率數據找出其規律，來推測未來月度嬰兒出生率的問題。

一、繪制序列時序

圖1為某城市月度嬰兒出生率序列時序。

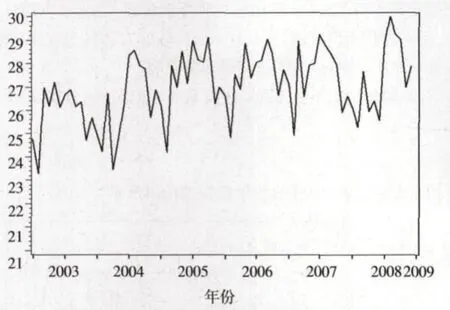
圖1 某城市月度嬰兒出生率序列時序

時序圖顯示該序列具有長期遞增趨勢和一年為周期的季節效應。根據時間序列的處理方法，要對其數據進行平穩性處理，因此下面一步要進行差分平穩化處理。

二、差分平穩化

對原序列作階步差分，希望提取原序列趨勢效應和季節效應，差分后序列時序如圖2所示。

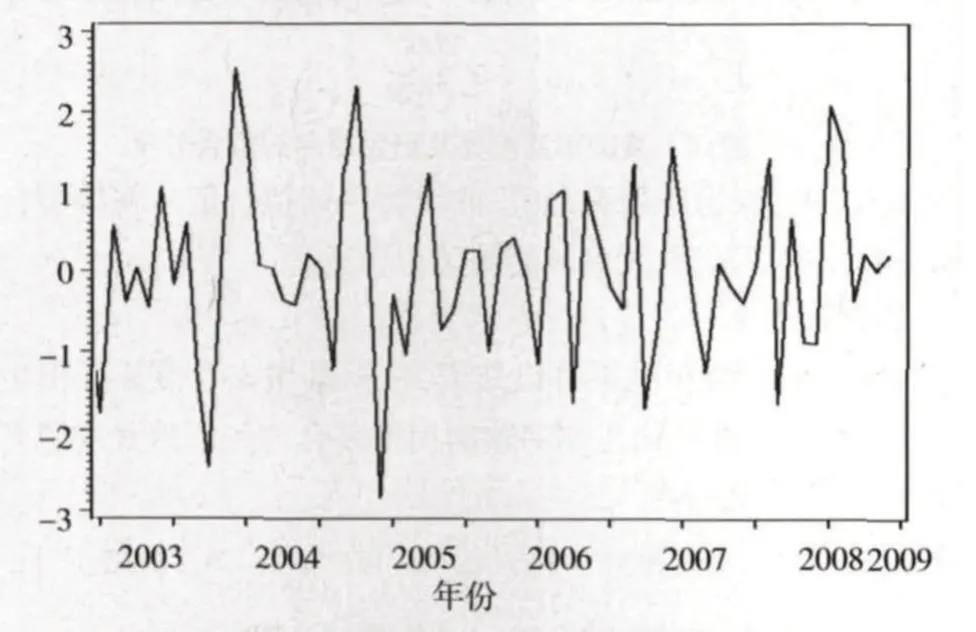
圖2 某城市月度嬰兒出生率階步差分后序列時序

該時序圖顯示差分后序列類似平穩。下面就要根據時間序列的相關知識進行模型定階。

三、模型定階

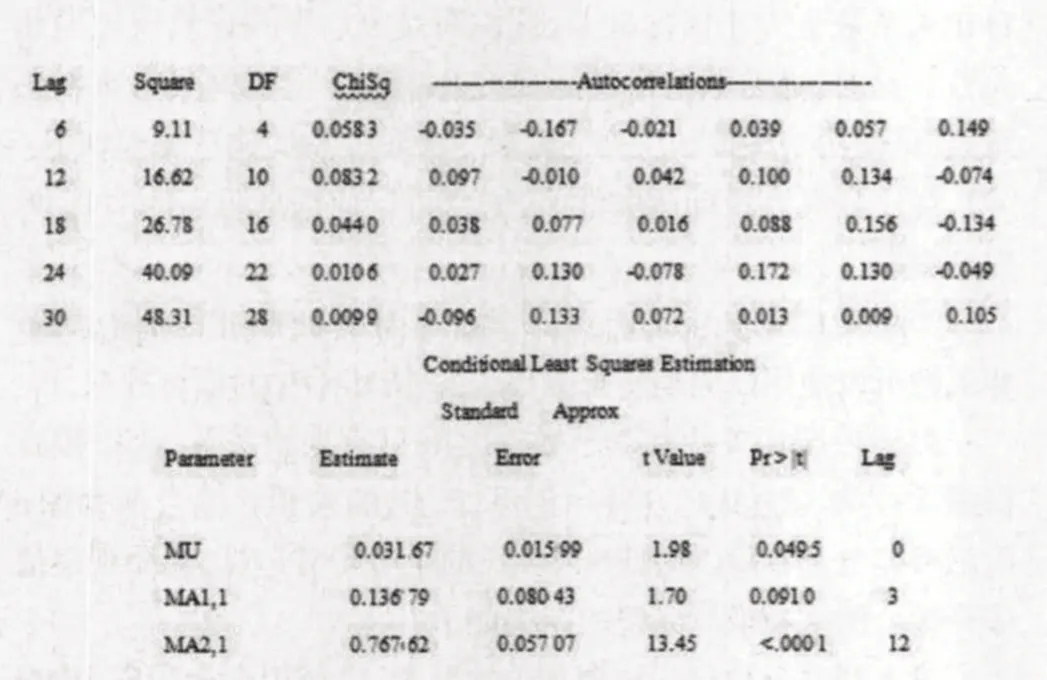
考察差分后序列自相關圖的性質，進一步確定平穩性判斷，并估計擬合模型的階數，如圖3所示。

圖3 某城市月度嬰兒出生率階步差分后序列自相關情況

自相關圖顯示延遲步自相關系數顯著大于倍標準差范圍，這說明差分后序列中仍蘊含著非常顯著的季節效應。延遲步的自相關系數也大于倍標準差，這說明差分后序列還具有短期相關性。這時，通常假定短期相關性和季節效應之間具有乘積關系，嘗試使用乘積擬和序列的發展。乘積模型的構造原理如下：

當序列具有短期相關性時，通常可以使用低階ARMA（P，Q）模型提取。

當序列具有季節效應，季節效應本身還具有相關性時，季節相關性可以使用以周期步長為單位的ARMA（P，Q）模型提取。

由于短期相關性和季節效應之間具有乘積關系，所以擬合模型實質為ARMA（P，Q）和ARMA（P，Q）的乘積。綜合前面的d階趨勢差分和D階以周期S為步長的季節差分運算，對原觀察值序列擬合的乘積模型完整的結構如下：

考慮到差分后序列短期相關性顯著，嘗試擬合乘積模ARMA（0，1，3）×（0，1，1）12，

下面，運用SAS程序進行參數的估計。

四、參數估計

使用條件最小二乘估計方法，確定該擬合模型的口徑為：

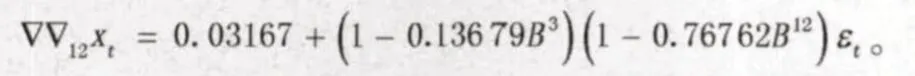
該模型適用顯著性水平大于0.1 的情況。下面對模型的準確性進行檢驗。

五、模型檢驗

對擬和模型進行檢驗，檢驗結果顯示該模型順利通過殘差白噪聲檢驗和參數顯著性檢驗。

將序列擬合值和序列觀察值聯合作圖，可以直觀地看出該乘積模型對原序列的擬合效果良好，如圖4所示。

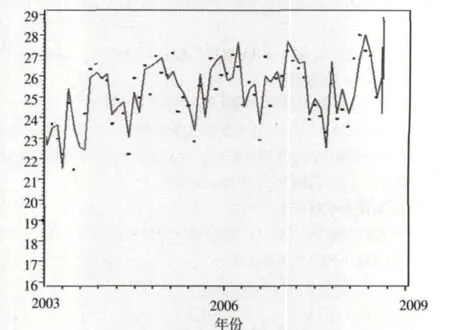
圖4 某城市月度嬰兒出生率序列擬合效果

圖4中，點為序列觀察值；曲線為序列擬合值。在模型合適的情況下進行預測，觀察預測圖是否合適。

六、預測

從上面的分析結果可以知道，根據某城市月度嬰兒出生率的數據的得到嬰兒出生率的預測模型是合理的。故月度嬰兒出生率的預測模型為：

模型適用顯著性水平大于0.1的情況。