大型轉子空間位置測量及自定位加工方法的研究

胡志勇，楊實禹，周文杰

（內蒙古工業大學 機械學院，內蒙古 呼和浩特 010051）

許多大型機電設備，如大型發電設備、重型機械、大型燃氣輪機與航空設備等，其中轉子類或大型回轉類零件占有很大比重。此類設備關系到國防、能源、交通、環保等國計民生，是具有巨大發展前景的高技術領域[1]。

由于多數大型轉子的結構復雜，形式多樣，而且尺寸精度和位置精度要求很高，傳統的加工工藝在前期加工裝夾及找正，比較困難且用時較長，嚴重影響整體加工周期，阻礙了生產效率的提高。

本文提出一種適用于大型轉子加工裝夾精度檢測及自定位加工方法。使用拉桿式直線位移傳感器測量轉子外圓，當轉子實際裝夾位置不與理想位置重合時，傳感器探頭產生位移，輸出位移信號。將位移信號進行處理擬合成位移曲線，再很據曲線建立轉子實際軸線位置數學模型，并計算轉子各加工位置坐標[2]。當轉子結構較為復雜、機床卡盤需多次旋轉對轉子多個面進行加工時，可用變換矩陣法計算轉子旋轉后各實際加工位置坐標[3]。再根據計算結果，修正原有數控程序，加工出符合圖紙要求的工件，實現自動定位加工的目的。

1 大型轉子的傳統加工方法

目前大型轉子數控加工的總工藝流程是：轉子裝夾→找正→基準加工→轉子掉頭找正→基準設置→轉子余量檢查→轉子加工→轉子掉頭找正→剩余部分加工→軸頸加工。

以上列出的是大型轉子數控加工的工藝流程，具體到每根轉子，又因為結構與用途不同，而工藝細節有異。多數大型轉子在數控機床上采用一夾一托方式，采用的找正方式與普通機床有較大差異，且難度較大[4]。

大型轉子在機床上的找正過程為：先找正轉子的中心高，再找轉子外圓跳動，最后找轉子左右偏斜，此過程要反復進行，最終達到找正目的。

2 大型轉子測量及位置坐標計算

2.1 大型轉子測量方法

由于轉子是回轉類零件，所以裝夾時出現的相對于理想位置的偏斜角及偏移量，都屬于空間位置變化，且大型轉子的重量大體積大，一次裝夾后不易對其進行找正調整（如圖1）。現階段采用傳統加工模式加工大型轉子時，用于裝夾及找正的生產準備時間，在總生產時間中所占比例很大。

圖1 大型轉子加工裝夾工位

結合實際條件及加工環境，筆者提出一種應用拉桿式直線位移傳感器測量轉子實際軸線位置的方法。將轉子裝夾在機床上，保持托架與卡盤水平。在轉子兩端選擇距機床坐標系原點距離分別為L1與L2的A、B 兩點為測量點并安裝直線位移傳感器（如圖2）。

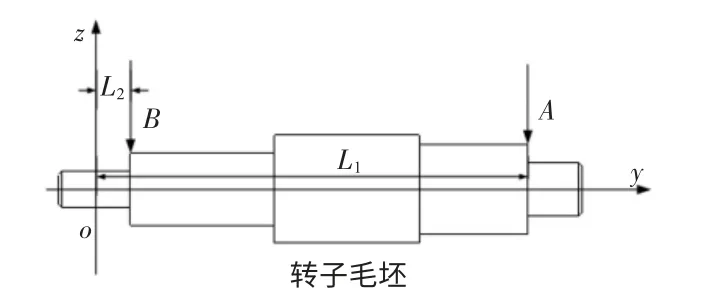
圖2 轉子毛坯測量位置簡圖

傳感器測量頭與轉子外圓直接接觸，控制卡盤帶動轉子緩慢勻速旋轉一周，當轉子實際位置與理想位置存在偏差時，測量頭產生位移，傳感器輸出位移信號，將提取到的位移信息存儲在寄存器中，再進行信號處理擬合成位移曲線（如圖3）。

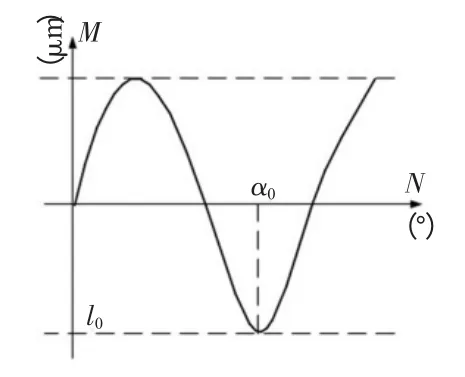
圖3 位移曲線示意圖

圖3坐標系中，M軸表示傳感器的位移距離，N軸表示大型轉子毛坯旋轉角度。由圖可知，位移曲線波谷α0位置處，為轉子毛坯最大偏心位置，所對應M軸上l0處的值，為轉子實際裝夾位置相對于轉子理想裝夾位置最大偏心距離。

2.2 轉子位置坐標算法

轉子是回轉類零件，對轉子進行銑削或車銑加工時，由于裝夾不同心產生的加工誤差，可看作在該位置轉子實際軸線相對于理想軸線的偏心距。通過上述測量結果，可以建立轉子軸線數學模型。

為方便觀察，將A、B 兩測量位置的轉子橫截面圓心a，b 投影至機床坐標系xz平面上。

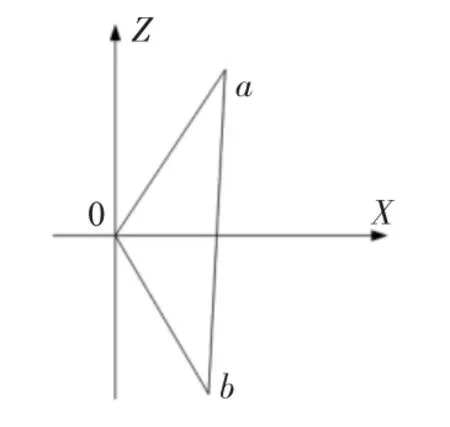
圖4 xz平面轉子軸線位置示意圖

設a，b 在機床坐標系中的坐標為

a：(x1，y1，z1)，

b：(x2，y2，z2)。

計算圓心a坐標，應用之前所述測量方法，可得到轉子最大偏心距l0及偏移角度α0，可得方程組

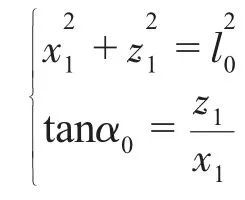
解方程可求出(x1，z1)，并根據之前測量結果可知a點坐標為（x1，L1，z1）

同理，可求出測量點B 處圓心坐標b:（x2，L2，z2）通過a、b 兩點的坐標，建立大型轉子軸線數學模型

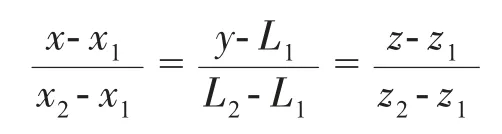
由此轉子軸線數學模型，可求出轉子實際軸線上任意一點坐標，即轉子任意橫截面圓心坐標。當轉子機構比較復雜，需對多個平面進行加工時，機床卡盤需進行多次旋轉。此時可通過初始坐標與變換矩陣相乘的算法，計算旋轉后的各圓心坐標。以A 測量點圓心a為例，以矩陣形式表示a點坐標

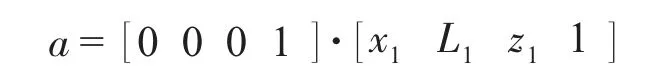
用T 來表示三維變換矩陣

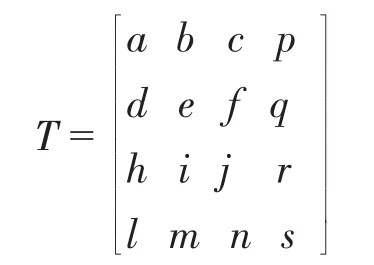
對于大型轉子而言，存在平移與旋轉兩種變換。以A點測量位置為例，設T1表示平移變換矩陣，T2表示旋轉變換矩陣。利用轉子軸線數學模型求出A點位置橫截面圓心坐標，可確定平移變換矩陣。

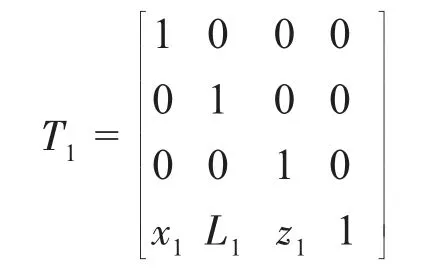
旋轉變換分為繞坐標軸旋轉變換和繞任意軸旋轉變換，可分解成繞x軸旋轉α角度的變換矩陣為T2x，繞y軸旋轉β角度的變換矩陣為T2y，繞z軸旋轉γ角度的變換矩陣為T2z，由于大型轉子軸線較長，角α 與角γ 相對與卡盤繞y軸旋轉角度β 較小，可忽略不計，所以可確定旋轉變換矩陣為

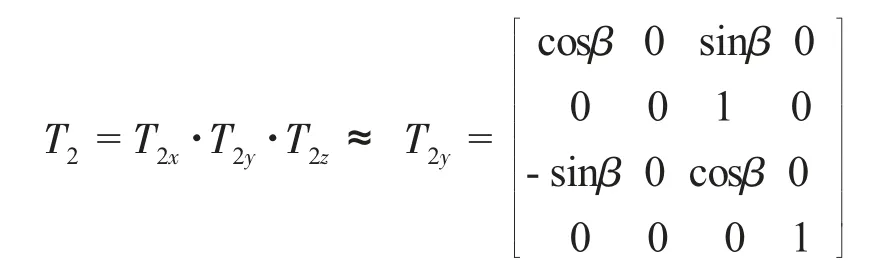
設點a'為經平移旋轉變換后轉子加工平面圓心的坐標，其計算過程為

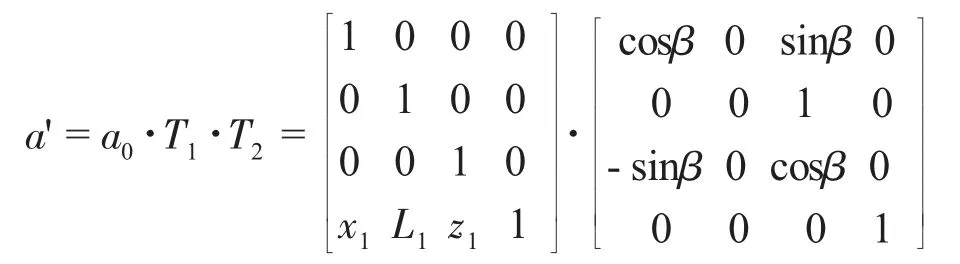
經計算，可求出此測量位置轉子橫截面圓心坐標。同理，可以基于此變換矩陣算法，求出轉子毛坯實際軸線上任意點坐標。

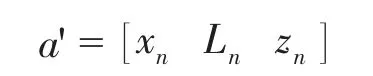
根據計算結果，修正原有數控程序

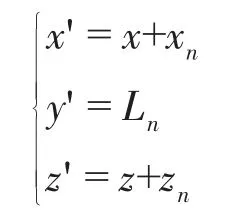
x'，y'，z'為修正后轉子數控加工代碼坐標值。

3 大型轉子自動定位加工流程

圖5為大型轉子裝夾精度測量及自定位加工流程。針對大型轉子加工環境及不易找正的現狀，本文提出采用位移傳感器安裝后不動，控制卡盤旋轉，測量轉子外圓，當轉子不處于理想加工位置時，測量頭產生位移傳感器輸出位移信號。根據輸出的信號擬合位移曲線，確定最大偏移角度及最大偏移量，并建立轉子軸線數學模型。

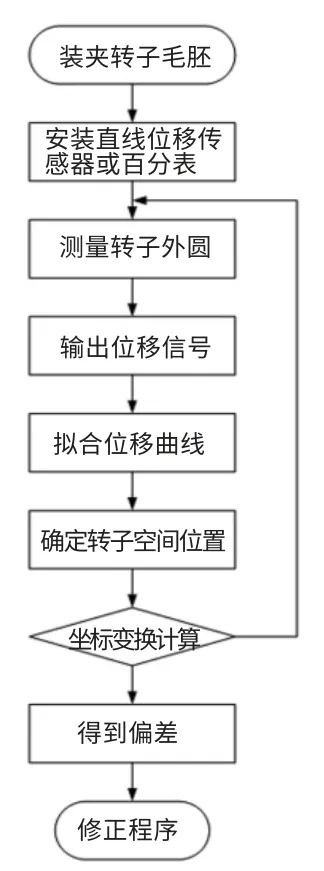
圖5 大型轉子裝夾精度測量及自定位加工流程圖

由軸線數學模型確定平移變換矩陣，由旋轉角度確定旋轉變換矩陣，利用變換矩陣算法，計算轉子軸線上任意點坐標，此坐標即是轉子相對于理想位置的偏移坐標。將此結果直接輸入計算機，修正原數控代碼坐標值，加工出符合要求的工件，實現自定位加工效果[6]。

當轉子結構復雜時，可反復計算多個平面及多個加工位置的偏移坐標。此過程可基于VB 或C++等高級編程語言，編寫轉換器實現計算偏移坐標及修正數控代碼的自動運行。

4 計算實例

現有大型轉子長L=9 742 mm，總質量t =100 t。

在轉子毛坯上選擇A、B 兩測量點，L1=9 800 mm，L2=920 mm。

應用上述方法對其進行測量，得

yA0=82 μm，yB0=61 μm，xA0=56°，xB0=312°。

經過計算，可求出A、B 兩測量點轉子橫截面圓心坐標

由a、b 兩點坐標，建立轉子軸線數學模型

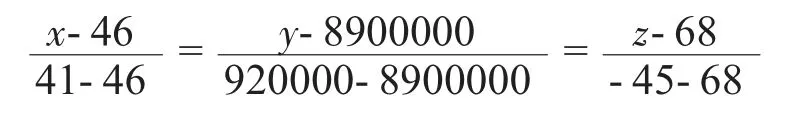
在轉子A 測量點位置需加工52個轉子葉片槽，此加工過程轉子卡盤需旋轉52次，每次旋轉6.9°。利用之前所述變換矩陣算法，可計算出轉子每次旋轉后A 處橫截面圓心坐標，如：經過一次旋轉后轉子圓心坐標為

由于轉子軸線方向偏差忽略，所以y軸坐標不變，根據此計算結果，可知卡盤經過一次旋轉后原有數控坐標應修正為

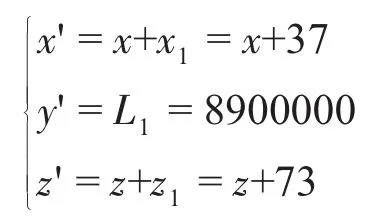
圖6為A點處x軸、z軸坐標與機床卡盤旋轉角度的曲線關系，橫軸為卡盤旋轉角度，縱軸為偏移距離。利用此算法可求出轉子任意位置偏移坐標，最終實現自定位加工。

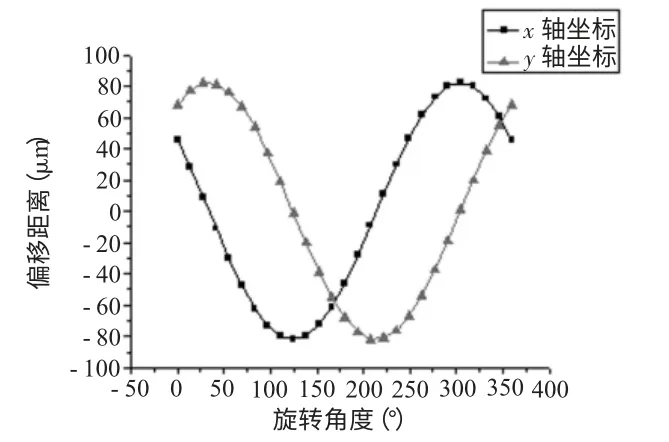
圖6 x軸y軸坐標變換曲線

5 結束語

本文提出了以加工工件為基準，通過測量轉子位置，計算轉子軸線坐標，修正原有數控程序，最終實現自動定位加工的新型數控加工方法，該方法可降低對大型轉子的裝夾要求，無需進行找正，簡便易行，可大大節省加工準備時間，對提高生產效率具有一定實際意義。

[1]韓 雷.重型燃氣輪機轉子切削加工工藝與變形控制[D].上海:上海交通大學,2009.

[2]毛德柱，周 凱，張伯鵬，等.智能尋位加工技術應用研究[J].制造技術與機床，2000，（4）：42-44.

[3]周 凱，毛德柱，張伯鵬.自尋位數控機床的研究[J].機械工程學報，2001，37(5)：48-52.

[4]桂啟志.轉子數控加工方法分析[J].重型機械科技，2003，（4）：22-25.

[5]譚光宇，隋天中，于鳳琴.機械CAD技術基礎[M].哈爾濱：哈爾濱工業大學出版社，2005.

[6]楊 莉，胡占齊.數控加工中工件的自動定位[J].制造技術與機床，2001，（4）：23-25.