直流調速系統穩定邊界法PID校正的設計與仿真

陳貴銀

（武漢船舶職業技術學院電氣與電子工程學院，湖北武漢 430050）

雖然直流電動機存在結構復雜、使用及維護成本較高的缺點，但具有調速范圍廣、靜差率小、穩定性好、過載能力大、能承受頻繁的沖擊負載、可實現頻繁的無級快速起制動和反轉等良好的動態性能，因此得到廣泛的應用。廣大研究工作者一直致力于各種控制方法的研究，以期進一步提高直流調速系統的性能。使用PID 校正是目前廣泛應用于直流調速系統有效的控制方法。一般的P I D 控制算法計算復雜，PID 的三個參數確定一直是難點，使用穩定邊界法確定PID 校正器的三個參數就可以簡化計算，確定起來方便，也很實用［1～2］。

1 穩定邊界法PID 校正原理

系統閉環特征方程的根（即閉環極點）都在其復平面虛軸的左側時，閉環系統穩定；當閉環特征方程有純虛根時，系統的根軌跡與虛軸相交，其響應等幅振蕩，系統臨界穩定；只要有一個閉環特征方程的根（即閉環極點）在其復平面虛軸的右側時，閉環系統不穩定。當置PID 調節器的T1＝∞與Td＝0時，增加kp直至系統開始振蕩，此時系統閉環極點應在復平面的jω軸上，確定系統閉環根軌跡與復平面jω軸交點，求出交點的振蕩角頻率ωn及其對應的系統增益km，則其PID 調節器參數的整定計算公式如表1所示。

表1 穩定邊界法PID 整定公式

為了實現用穩定邊界法整定公式計算系統P、PI、PID 校正器的參數，在MATLAB中編寫函數文件，下面給出函數Zn02（）。其格式為［Gc，Kp，Ti，Td］＝zn02（PID，G，p），其中PID 是校正器的類型，當PID＝1 時，為計算P 調節器的參數；當PID＝2 時，為計算PI調節器的參數；當PID＝3 時，為計算PID 調節器的參數。輸入參量G 是已知被校正系統的開環傳遞函數，輸入參量p為系統開環極點的個數（不計重根數，即多重根只計為1 個根）。輸出參量Gc為校正器傳遞函數，Kp為校正器的比例系數；Ti為校正器的積分時間常數；Td為校正器的微分時間常數。如果要使用該函數，則將其存放在MATLAB7.1＼Work的路徑與子目錄下，以便查找及調用［3～4］。

2 直流調速系統的組成

直流調速系統的組成框圖可參見圖1所示。由圖1 可見，該系統的控制對象是直流電動機M，被調量是電動機的轉速n，晶閘管觸發電路和整流電路為功率放大和執行環節，由運算放大器構成的比例調節器為電壓放大和電壓（綜合）比較環節，電位器RP1為給定元件，測速發電機TG與電位器RP2為轉速檢測元件，此外還有由取樣電阻RC、二極管VD 和電位器RP3構成的電流截止負反饋環節［3］。

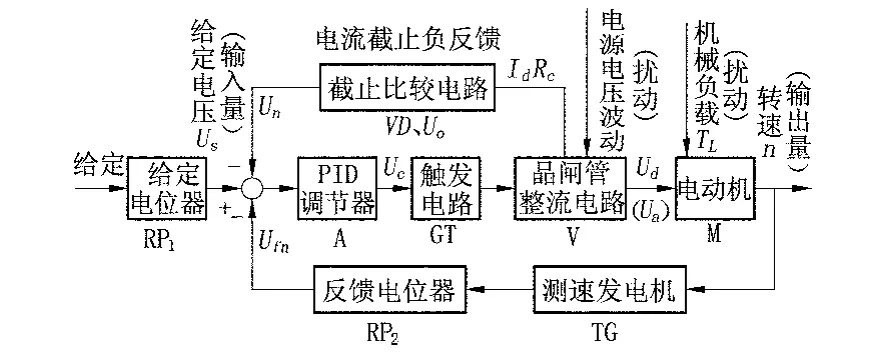
圖1 直流調速系統的組成框圖

3 直流調速系統穩定邊界PID 校正法的仿真設計

現將上述直流調速系統原理框圖進行簡化成如圖2所示結構圖，已知固有的控制系統參數如下。

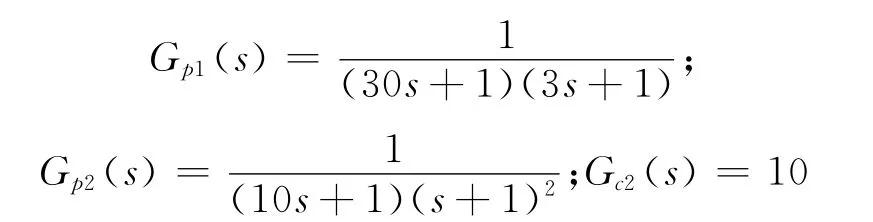
下面用穩定邊界法計算系統主調節器Gc1（s）P、PI、PID 校正時的參數，并進行階躍給定響應的仿真。

圖2 直流調速系統簡化結構圖

根據題意，利用zn02（ ）函數求系統PI校正器參數的程序L621.m 如下。

程序須在MATLAB 命令窗口中運行，程序運行后有根軌跡圖3所示，圖上顯示有十字光標，選擇根軌跡與虛軸的交點用鼠標左鍵點擊。再回到MATLAB 命令窗口中，可以見到有計算出的根軌跡增益與極點值（應該力求準確定在根軌跡與虛軸的交點上，盡量使極點實部為0），還可見到字符“K”。應該在字符“K”后鍵入指令“return”后并按下回車鍵，然后即可在MATLAB命令窗口中看到km＝1.1436，ωm＝0.1646，這就是交點的系統增益km及其對應的振蕩角頻率ωm。在MATLAB命令窗口中還看到用穩定邊界法計算出P、PI、PID 校正的參數。再彈出根軌跡圖，再次鼠標左鍵點擊根軌跡與虛軸的交點，程序三次調用函數zn02.m，即這樣操作三次，最后得到如圖4 所示的PID 三種校正時的階躍給定響應曲線與校正器計算結果。

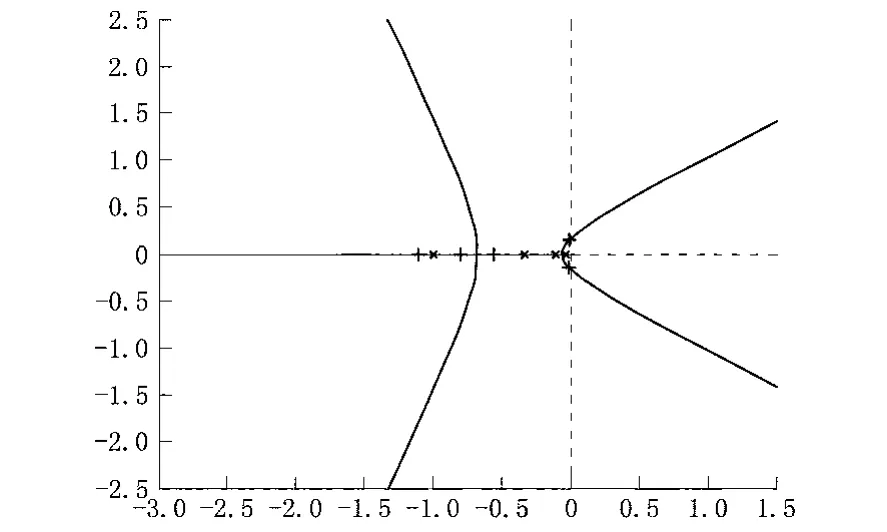
圖3 系統閉環根軌跡圖

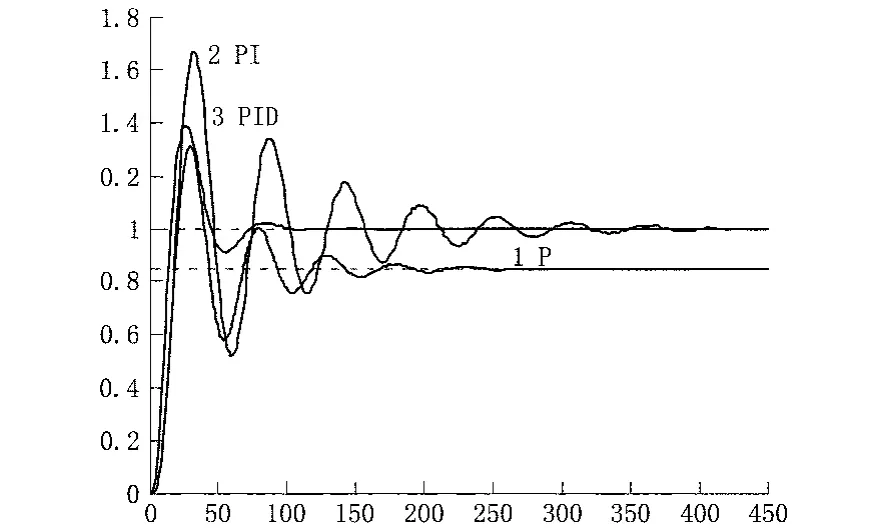
圖4 PID 三種校正階躍給定響應

計算出三種P、PI、PID 校正時校正器的參數分別為：

①P校正器：Gc1＝Kp1＝0.4682

②PI校正器：KP2＝0.5203；Ti2＝32.4395

③PID 校正器：KP3＝0.6861；Ti3＝19.0821；Td3＝4.7705

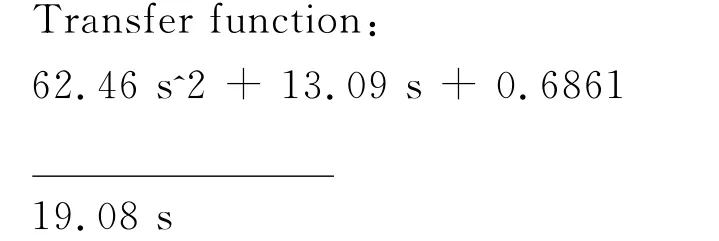
從圖4所示穩定邊界法計算的P、PI、PID 校正階躍給定響應曲線看到，P與PI校正的躍響應曲線上升的速度差不多快，PID 校正得最快；三條曲線有兩個不同的終了值。超調量都較大，以PI校正的為最大［5］。

4 結 語

本文提出了采用穩定邊界法的思想去仿真設計直流調速系統PID 調節器，通過以上具體的仿真實例，說明在控制系統的穩定性、快速性與精度三大性能不能滿足系統需要時，需設置PID 調節器，而PID 調節器的三個參數Kp，Ti與Td的整定一直是個難點，運用穩定邊界法較好地解決這一問題，從以上調試仿真的結果來看，控制系統的動態性能與穩態性能都很理想，控制方法方便實用，值得推廣。

1 楊祖元.雙閉環直流調速系統模糊PID 控制研究［J］.計算機應用研究，2011（3）.

2 王玉德.模糊PID 的設計與仿真［J］.電子技術設計與應用，2010（4）.

3 孔凡才.自動控制原理與系統［M］.北京：機械工業出版社，2008.158

4 黃忠霖.自動控制原理MATLAB 的實現［M］.北京：國防工業出版社.2008.257

5 代忠.基于數字PID電阻熱爐溫度控制系統的設計［J］.高教論述.2011（5）