一種新的子空間更新算法在DOA估計中的應用

胡茂兵，湯煒，蔡燦輝

（華僑大學 信息科學與工程學院，福建 廈門 361021）

一種新的子空間更新算法在DOA估計中的應用

胡茂兵，湯煒，蔡燦輝

（華僑大學 信息科學與工程學院，福建 廈門 361021）

為改進傳統算法對突變信號跟蹤慢的缺點，提出一種有效的可變遺忘因子的子空間更新算法——逼近特征分解方法.該算法采用可變遺忘因子對陣列輸出信號協方差矩陣進行秩－1更新，在該協方差矩陣特征分解的基礎上，結合先驗信息構造新的代價函數，并利用該代價函數的最小二乘解實現對信號子空間的實時更新.仿真結果表明：新算法的波達方向估計誤差僅為原算法的1／5，而對突變信號的跟蹤速度達到原算法的5倍，證實該算法的準確性和有效性.

波達方向；突變信號；可變遺忘因子；子空間更新算法；特征分解

隨著信息時代的到來，國內外學者提出利用智能天線技術解決現階段頻譜資源匱乏的問題［1-2］.近年來，波達方向（DOA）估計作為智能天線應用中的關鍵技術已得到廣泛的關注并提出許多DOA估計算法.但這類算法不能對相干信源進行DOA估計，而在CDMA通信系統中這類相干信源是普遍存在的［3］.Pillai等［4］融合前后向空間平滑技術改進了這一缺陷.此外，這類算法屬“批處理”算法，即在獲得所有快拍數據后一次性處理.顯然，這種“批處理”算法僅適用于非時變系統和平穩信號［5-6］，而在實際環境中存在大量時變系統和非平穩信號，如仍采用上述算法進行DOA估計，則傳統方法就會失效.針對子空間更新的問題，Yang等［7-8］提出了近似投影子空間跟蹤（PAST）算法與緊縮近似投影子空間跟蹤（PASTd）算法，這類方法由于其收斂速度快而得到廣泛應用.然而，該方法得出的子空間正交性不強.Meraim等［9］隨后提出了改進的OPAST算法.這一系列類算法均未考慮信號的相干性和遺忘因子的可變性等問題，致使方法的應用范圍受到限制.本文在傳統算法的基礎上對遺忘因子和代價函數進行了優化和改進，提出了一種新的子空間更新算法——逼近特征分解方法.

1 陣列信號模型

考慮陣元數M的均勻線陣（ULA），陣元間距d＝λ／2，采樣快拍數為pd，接收來自D不同方向θ＝［θ1，θ2，…，θD］的窄帶信號S（t）＝［s1（t），s2（t），…，sD（t）］T.假定 D先驗已知，定義信號到達角θ為信號傳播方向與ULA法向的夾角，陣列天線模型如圖1所示，則第k個快拍時刻陣列接收信號［10］為）

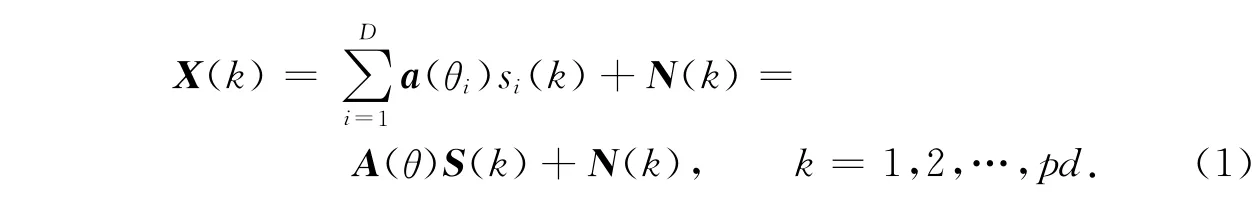
式中：X（k）＝［x1（k），x2（k），…，xM（k）］T為 M 個陣元的接收信號矢量，a（θi）＝［1，exp（－jφi），…，exp（－j（M－1）φi）］T為 ULA與信號si（k）對應的導引向量；N（k）＝［n1（k），n2（k），…，nM（k）］T為 M 個陣元接收的與信源無關且相互獨立的高斯白噪聲；φi＝（2πdsinθi）／λ；A（θ）＝［a（θ1），a（θ2），…，a（θD）］為ULA導引矩陣.

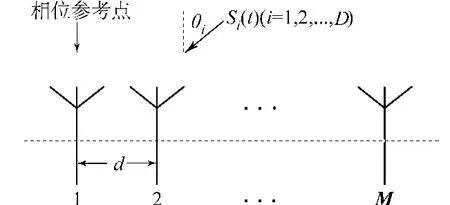
圖1 M元均勻線陣模型Fig.1 Model of the ULA with Msensor elements

2 逼近特征分解的子空間更新算法

考慮子空間類算法中，協方差矩陣“批處理”性質無法實現時變信號的DOA跟蹤，Yang等［7］提出了投影逼近子空間跟蹤（PAST）算法，其陣列輸出信號協方差矩陣R（k）＝E［X（k）XH（k）］的代替式為

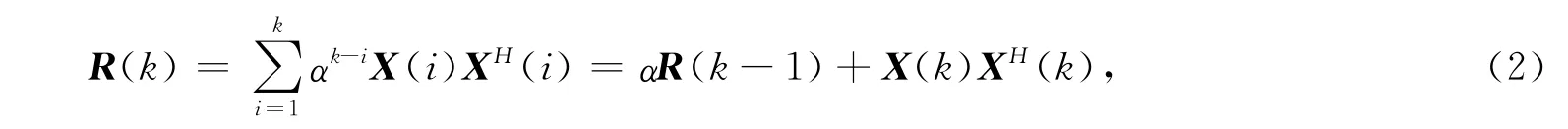
式（2）中：α為遺忘因子，反映的是原有數據在R（k）更新過程中所占的比重.當α較大時，原有數據保留較多，相應的實時數據所占比例下降，協方差矩陣更新速度較慢；而當α較小時，原有數據保留較少，實時數據所占比例增加，雖然協方差矩陣更新速度加快，但數據量不足，使得估計性能易受噪聲影響，估計誤差較大.所以對于具有恒定遺忘因子的算法（如PAST算法），無法同時獲得較快的收斂速度和較小的穩態DOA跟蹤誤差.

針對陣列輸出信號協方差矩陣秩－1更新式（2）中固定遺忘因子α所帶來的性能缺陷，提出一種新的方程，即

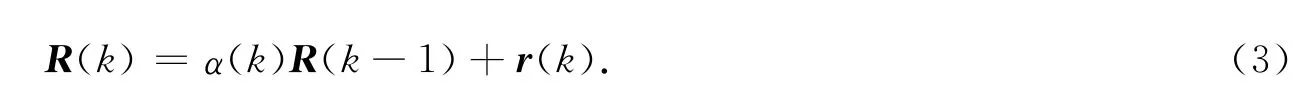
式（3）中：r（k）＝X（k）XH（k）.與傳統子空間更新算法不同，它采用的是可變遺忘因子，即α（k）＝｛α1，α2｝，且α1＜α2.假設在快拍時刻K1時信號DOA發生突變，此時令α（k）＝α1，其余時刻α（k）＝α2.這樣對于突變信號，既可以獲得較快的跟蹤速度，又可以獲得較低的穩態估計誤差.

為了適用于相干信號源的情況，對式（3）中的協方差矩陣R（k）進行前后向平滑處理，即

隨著職業教育的發展，中職學校英語學科成為一門必修學科，英語口語表達成為一項必備的語言技能。然而，英語又是中職學生學習最為吃力的學科之一，大多數學生為此備受打擊，已不再奢望能學好英語，處在進退維谷的尷尬境地。由此，要重點樹立學生學習英語的信心和勇氣，培養學生學習英語的興趣，在教學中注入情感，用發展的眼光看待學生。同時借鑒專業教學的理念，任務引領、驅動，明確學習目標，搭建師生互動學習的平臺和學生展示的舞臺。再者，要尊重學生、愛護學生，建立和諧的師生關系，采用靈活的教學方法，定制學生的學習任務，讓每個學生學有所獲。

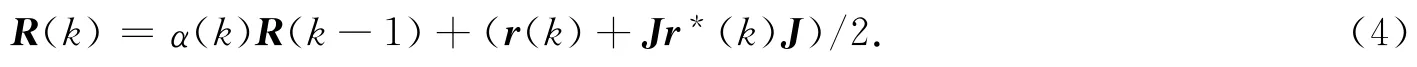
式（4）中：J為M 維交換矩陣，其反對角線上的元素為1，其余元素為0.對平滑處理后的R（k）進行特征分解，有

式（5）中：ΛS（k），ΛN（k）分別為由較大的D個特征值和較小的M－D個特征值構成的對角矩陣，對應的特征向量組成的矩陣US（k），UN（k）分別構成信號子空間和噪聲子空間，且存在如下關系，即

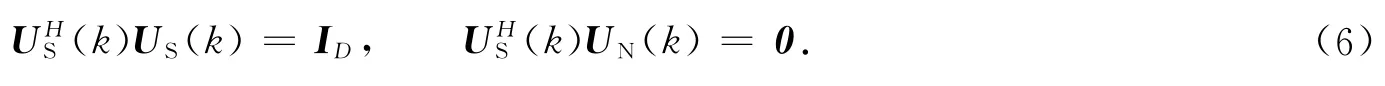
式（6）中：ID為D 維單位矩陣.對式（5）等號兩邊分別右乘US（k），UN（k），并利用性質（6），可得

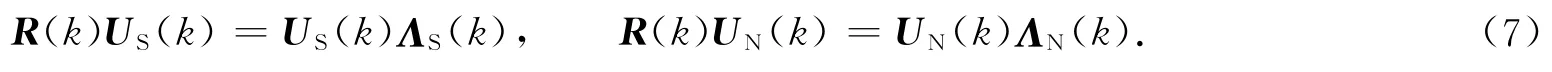
將方程組（7）可等效為

式（8）中：U（k）為M×r矩陣 .當r＝D時，U（k）代表信號子空間；而當r＝M－D時，U（k）代表噪聲子空間.利用先驗信息可得估計誤差為

式（9）中：h（k）＝UH（k－1）X（k）為X（k）在U（k－1）所張空間上的投影.由遞歸最小二乘法可得子空間更新模型為

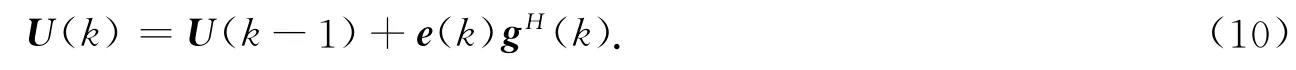
在式（8）中，利用先驗信息U（k－1）逼近U（k），可構造新的代價函數為

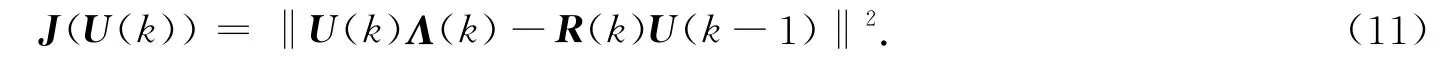
其中：約束條件U（k）HU（k）＝Ir.由于式（11）中的Λ（k）是由陣列輸出信號協方差矩陣的特征值構成的對角矩陣，為了避免特征分解，減少算法運算量，Λ（k）可以通過迭代來實時更新，即

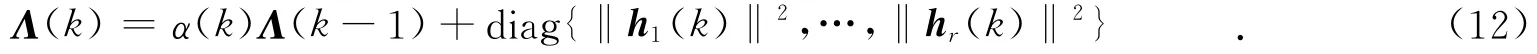
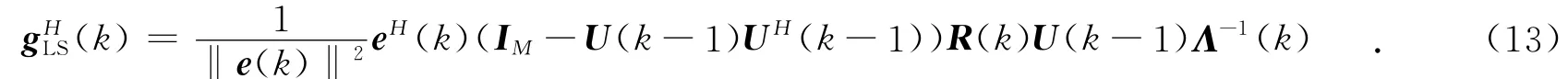
利用式（9）和式（13），可將gHLS（k）化簡為

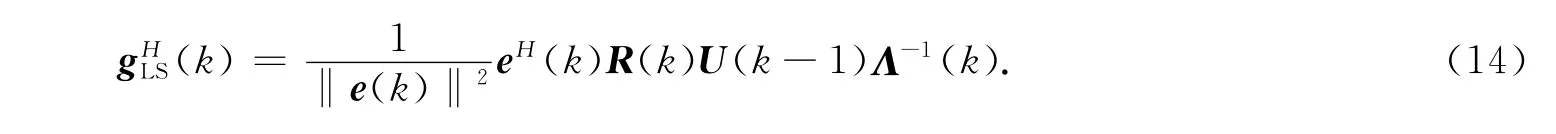
將式（14）代人式（10），結合式（9）可以實現對子空間U（k）的更新.然而，按式（10）得到的更新子空間并非完全正交的，需采用Gram－Schmidt方法對其正交化處理.

鑒于LS－ESPRIT算法具有不需譜峰搜索的優點［11］，故將更新后的子空間U（k）運用于LS－ESPRIT算法，就可以對時變信號進行DOA跟蹤.

式（3）中的信號突變時刻k1可以通過式（9）中的估計誤差e（k）確定，共有4個步驟：1）假定算法在k0時刻收斂，取1≤k≤k0時刻對應‖e（k）‖的最大值emax，即令emax＝max（‖e（1∶k0）‖）；2）用emax對k0＜k＜pd時刻所對應的‖e（k）‖進行歸一化處理，可得到，即有＝‖e（k）‖／emax；3）令c（k）＝；4）若c（k2）／c（k2－1）＞δ（δ為常數），則認為k2是k1的估計值.

在子空間更新類算法中，初始值R（0），U（0），Λ－1（0）的選取必須適當 .根據各矩陣的性質，最方便的選取即令R（0），Λ－1（0），U（0）分別為M×M和r×r的單位矩陣，以及M×M的單位矩陣的前r列.

3 仿真結果及分析

3.1 遺忘因子的選擇

仿真參數：ULA陣元數M＝8，陣元間距d＝λ／2，采樣快拍數pd＝400，信號源數D＝3，子空間維數參量r＝D.考慮3個非相關正弦信號源，頻率分別為1，3，2GHz，初始相位均為0，采樣頻率fs為10GHz.其中：信號1為非時變信號，DOA＝0°，信噪比為0dB；信號2為慢變信號，每次快怕間信號角度變化0.025°，信噪比為5dB，起始角度為30°；信號3為每次快怕間信號角度變化0.1°的快變信號，信噪比為5dB，起始角度為40°.

不同遺忘因子對應的穩態快拍數（pd）和最大DOA估計誤差（emax）仿真結果，如表1所示.從表1可以看出：穩態快拍數和最大DOA估計誤差與前文分析吻合，即α較大時，算法趨于穩態速度較慢，估計誤差較小；而α較小時算法趨于穩態速度較快，估計誤差增加.綜合考慮這兩方面因素，分別選擇α1和α2為0.60和0.85.

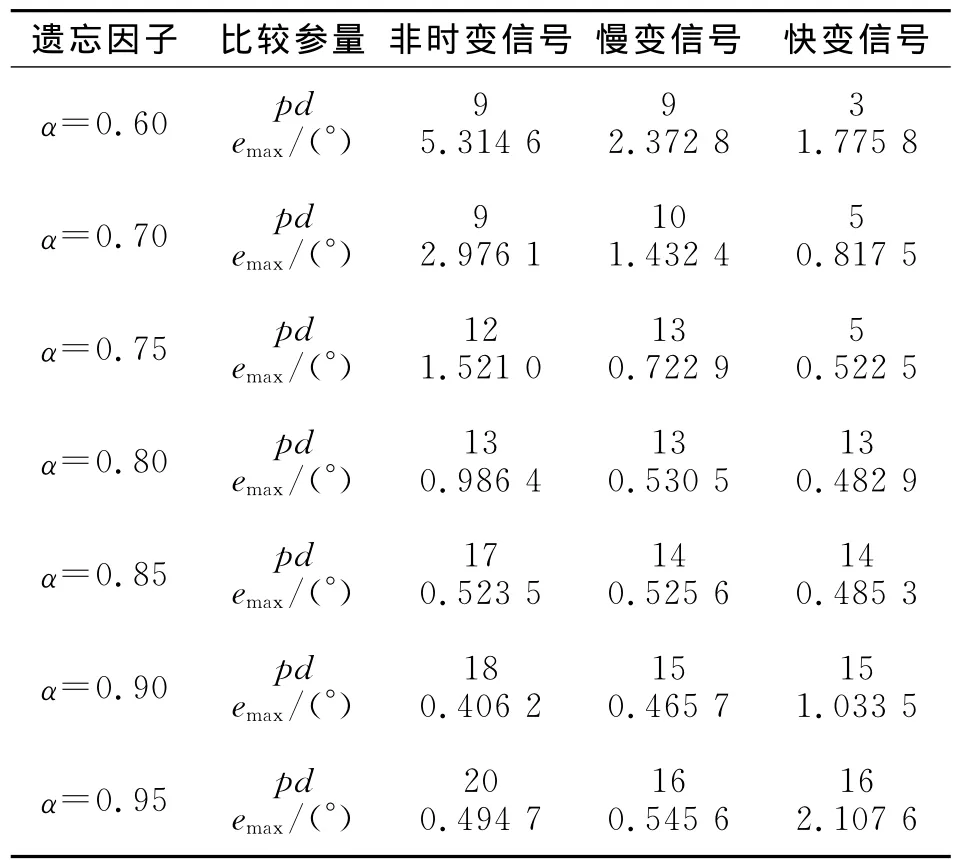
表1 不同遺忘因子的仿真實驗結果Tab.1 Simulation results for different forgetting factors

3.2 對非相關信號的DOA跟蹤

仿真信號模型與算例3.1相同，結果如圖2所示.圖2中：α＝｛0.60，0.85｝.由圖2可以看出：新算法不僅能對非時變信號和慢變信號進行精確DOA估計，對快變信號也能得到良好估計.

將該算法與PAST和特征值分解（ED）算法進行比較，得到的快變信號跟蹤誤差（e）曲線，如圖3所示.其中：ED算法中的信號子空間是直接對式（4）中的協方差矩陣進行特征分解得到的.

從圖3中可以看出：對快變信號而言，提出的算法與ED算法具有相似的跟蹤特性，對應的DOA誤差均約為PAST算法的1／5.這說明由該算法得到的信號子空間更接近于理想信號子空間，即ED算法中的信號子空間.

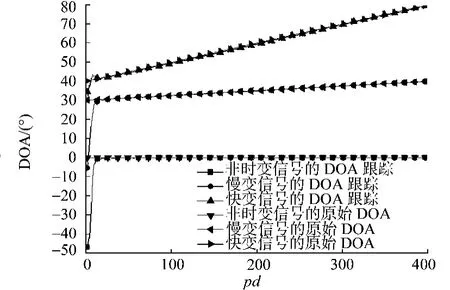
圖2 算法的跟蹤特性曲線Fig.2 Tracking characteristic curve of this algorithm

3.3 對突變信號的跟蹤性能分析

考慮單一正弦信號源，其頻率為f1＝1GHz，初始相位為0，采樣頻率fs＝10GHz.起始角度0°，采樣時刻為200時，信號源角度突變成10°，即k1＝200，k0＝20，常數δ＝17.按照提供的對突變時刻k1估計的方法，測得k1的估計成功概率（P）與信噪比（SNR）的關系，如圖4所示.由圖4可知：隨著信噪比的增加，對突變時刻k1的估計成功概率逐漸接近100%，說明提供的對突變時刻k1估計方法的有效性.

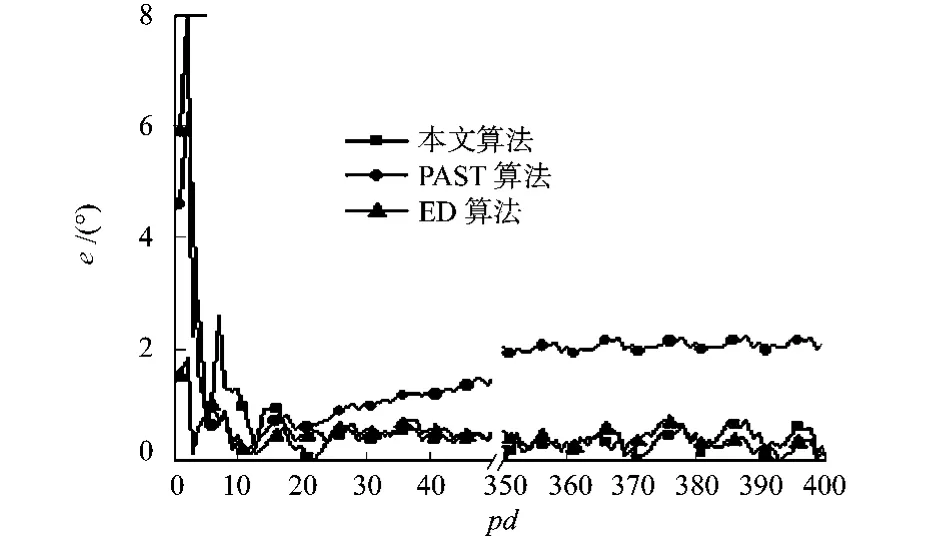
圖3 幾種算法對快變信號跟蹤誤差特性比較Fig.3 Tracking error eurve about rapidly varying time signal compare with algorithms

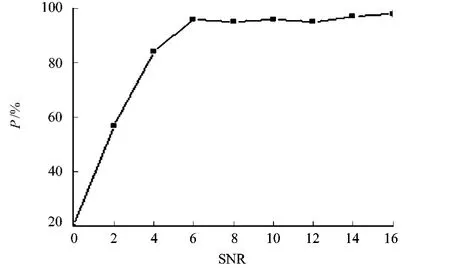
圖4 估計成功概率與信噪比的關系曲線 Fig.4 Successful probability estimation versus the SNR

選取單一正弦信號源，其信噪比為5dB，將所提出的算法與PAST算法對突變信號DOA跟蹤特性進行比較，如圖5所示.為了驗證可變遺忘因子對突變信號DOA跟蹤的有效性，將PAST算法分為PAST恒定α算法和PAST可變α算法，即PAST算法步驟中的α是可變的.

從圖5可以看出：所提出的可變遺忘因子算法對突變信號的DOA跟蹤速度最快，為PAST算法跟蹤速度的5倍；并且，由PAST兩類算法的跟蹤速度可以進一步驗證可變遺忘因子類算法在子空間更新算法中的優勢.

3.4 對相干信號的DOA跟蹤

設有3個正弦信號源，頻率分別為f1＝1GHz，f2＝1GHz，f3＝2GHz，其他仿真條件與算例3.1完全相同.由這3個信號源的頻率關系可知：信號2（慢變信號）是信號1（非時變信號）的相干信號，均為信號3（快變信號）的非相關信號.此時所得到的DOA跟蹤曲線，如圖6所示.從圖6可以看出：由于所提算法對陣列輸出信號的協方差矩陣進行了前后向平滑處理，而PAST算法未考慮信號相干性的影響，所以算法能實現對相干信號的DOA跟蹤.

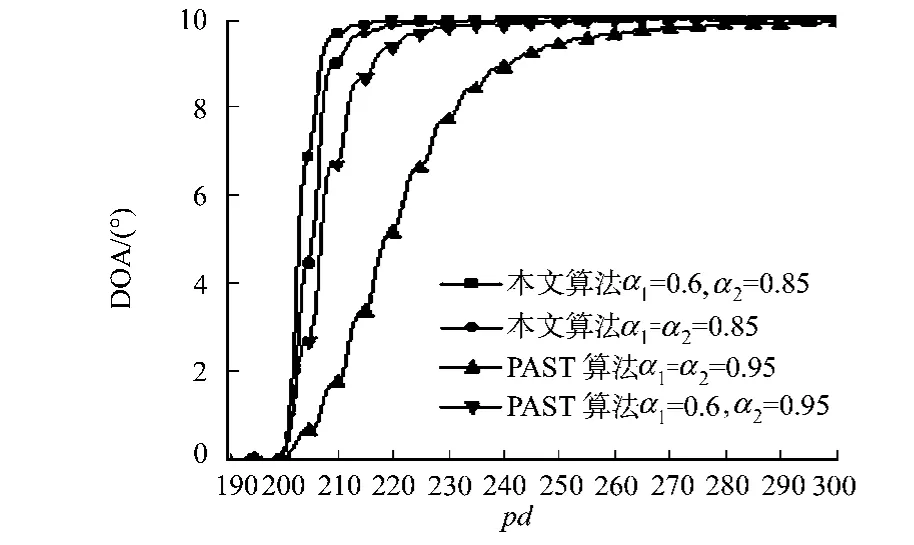
圖5 兩種算法對突變信號的跟蹤特性曲線Fig.5 Tracking the sudden parameter changing signals compared with the two algorithms

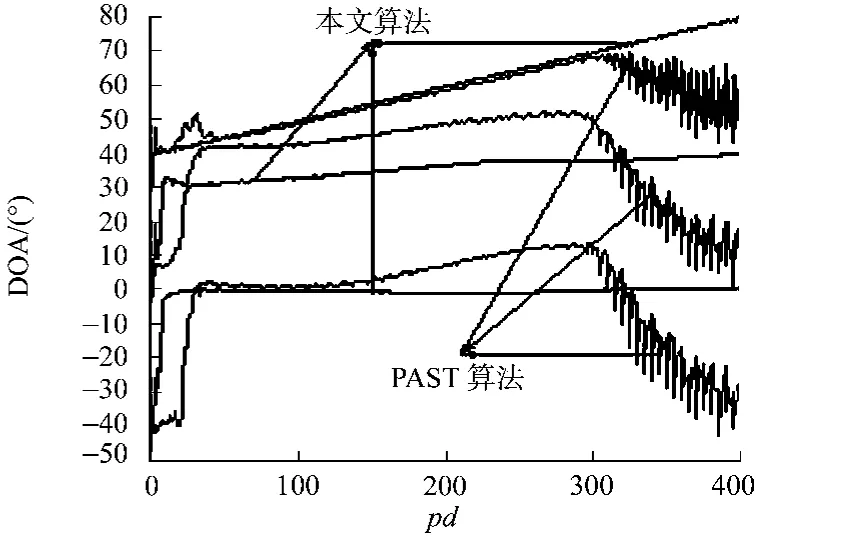
圖6 對相干信號源DOA估計比較曲線圖 Fig.6 Tracking the coherent signals compared with PAST algorithm

4 結束語

通過對遺忘因子在子空間更新算法中物理意義進行分析，得出可變遺忘因子可以加快算法對突變信號的DOA跟蹤速度的結論 .結合前后向空間平滑技術及新的代價函數，提出了一種適用性更為廣泛、快速高效的新算法——逼近特征分解算法.對連續時變信號而言，新算法的DOA跟蹤誤差僅為PAST算法的1／5；另一方面，對突變信號而言，該算法的跟蹤速度達到傳統算法的5倍，同時還克服了PAST算法無法對相干信號進行DOA跟蹤的缺陷.

［1］JIAN Huan，LIU Jian－fei.Application study of dual－polarization smart antenna in TD－SCDMA system［C］∥IEEE Trans on International Conference on Measuring Technology and Mechatronics Automation.Changsha：IEEE Press，2010：679－682.

［2］WINTERS J H.Smart antenna techniques and their application to wireless ad hoc networks［J］.IEEE Wireless Communications，2006，13（4）：77－83.

［3］WANG Li－xin.The DOA tracking method based gaussian particle filter in smart antennas［C］∥IET International Conference on Wireless，Mobile and Multimedia Networks.Hangzhou：IEEE Press，2006：1－4.

［4］PILLAI S U，KWON B H.Forward／backward spatial smoothing techniques for coherent singal identification［J］.IEEE Transactions on Acoustics，Speech and Signal Processing，1989，37（1）：8－15.

［5］TAO Guo－zheng.Recursive subspace model identification based on orthogonal projection and principal component analysis［C］∥IEEE International Conference on Computer Application and System Modeling.Taiyuan：IEEE Press，2010：422－429.

［6］TU Chao－cheng，CHAMPAGNE B.Subspace tracking of fast time－varying channels in precoded MIMO－OFDM systems［C］∥IEEE International Conference on Acoustics，Speech and Signal Processing.Taipei：IEEE Press，2009：2565－2568.

［7］SARKAR T K，YANG X.Application of the conjugate gradient and steepest descent for computing the eigenvalues of an operator［J］.IEEE Transactions on Signal Processing，1989，17（1）：31－38.

［8］YANG B.Projection approximation sbspace tracking［J］.IEEE Transactions on Signal Processing，1995，43（1）：95－107.

［9］ABED－MERAIM K，CHKEIF A，HUA Y.Fast orthonormal PAST algorithm［J］.IEEE Transactions on Signal Processing，2000，7（3）：60－62.

［10］王永良，陳輝，彭應寧，等.空間譜估計理論與算法［M］.北京：清華大學出版社，2004.

［11］LAVATE T B，KOKATE V K，SAPKAL A M.Performance analysis of MUSIC and ESPRIT DOA estimation algorithms for adaptive array smart antenna in mobile communication［J］.IEEE International Conference on Computer and Network Technology.Bangkok：IEEE Press，2010：308－311.

Application of a New Subspace Updating Algorithm in DOA Estimation

HU Mao－bing，TANG Wei，CAI Can－hui

（College of Information Science and Engineering，Huaqiao University，Xiamen 361021，China）

In order to improve the weakness of the traditional methods on tracking sudden parameter changing signals slowly，the approximation eigenvalue decompositionan method，an efficient subspace updating algorithm with variable forgetting factor，is presented.The novel algorithm adopts a new rank＿1updating equation with variable forgetting factors to update the covariance matrix of the array output signals.At the same time it proposes a new cost function which is based on the prior information and the eigenvalue decomposition（ED）of the updated covariance matrix.And then the signal subspace is updated real time by the least square solution of the new cost function.Finally，some examples are simulated and the results exhibit that the algorithm provides not only one fifth of the direction of arrival estimation error，but also five times of the tracking speed of sudden parameter changing signals to the original algorithm，which confirms the accuracy and effectiveness of this new algorithm.

arrival direction；sudden parameter changing signals；variable forgetting factor；subspace updating algorithm；eigenvalue decomposition

黃曉楠 英文審校：吳逢鐵）

TN 911.7

A

1000－5013（2012）04－0375－05

2011－08－29

湯煒（1974－），男，副教授，主要從事電磁場數值算法的研究.E－mail：tangwei74＠hqu.edu.cn.

福建省高校服務海西建設重點項目（2009HZ0008）