習(xí)題教學(xué)

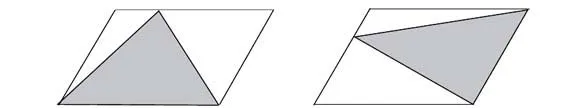
　　小學(xué)數(shù)學(xué)教材中的習(xí)題是學(xué)生進(jìn)行有效學(xué)習(xí)的重要載體，但大部分卻是“界定良好”的問題，即目標(biāo)明確、解決問題所需要的所有信息已得到呈現(xiàn)、只有一個(gè)正確答案的常規(guī)問題。如何讓習(xí)題變?yōu)椤昂玫摹⒂袃r(jià)值的”問題，凸顯教材意圖，使習(xí)題中隱含著的一些有價(jià)值的因素能夠被充分開發(fā)與利用，有效引領(lǐng)數(shù)學(xué)思維，本文做了一些嘗試與探索。
　　一、適當(dāng)放大問題思考空間，從“唯一”走向“多向”
　　在教學(xué)活動(dòng)中，學(xué)生是活動(dòng)的主體，在提供鞏固應(yīng)用知識(shí)的練習(xí)材料時(shí)，要對(duì)習(xí)題進(jìn)行充實(shí)、重組和處理，給學(xué)生創(chuàng)設(shè)較廣闊的利用知識(shí)進(jìn)行推理、判斷的思維空間。
　　【案例1】 蘇教版五（上）第18頁(yè)
　　10.下圖中每個(gè)平行四邊形的面積都是50平方厘米，
　　涂色的三角形面積各是多少？為什么？
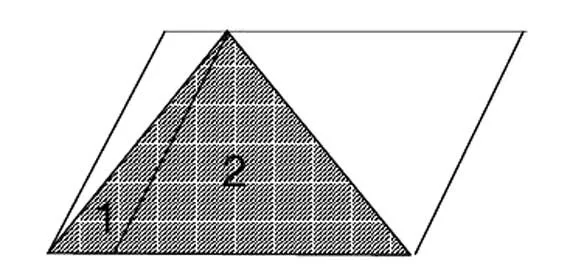
　　師：（直接出示圖1）猜猜陰影三角形的面積與平行四邊形的面積有什么關(guān)系。你能證明嗎？
　　經(jīng)過幾分鐘的自主探索和小組交流后，學(xué)生發(fā)言。
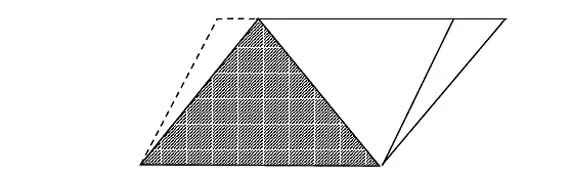
　　生1：可以將左邊的小三角形剪下拼在右邊。
　　生1上黑板演示：
　　生1：這樣陰影三角形的面積就是新平行四邊形面積的一半，也就是原來平行四邊形面積的一半。
　　師：將原來的平行四邊形等積變形成另一個(gè)平行四邊形來解決問題的想法非常好。
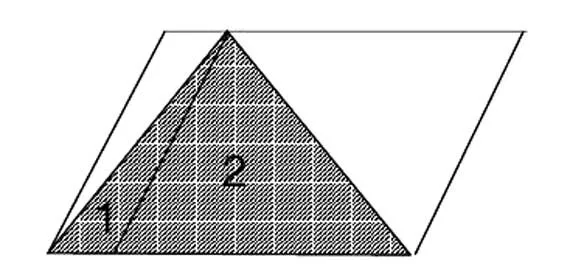
　　生2：我可以將這個(gè)大平行四邊形分割成兩個(gè)小平行四邊形。演示如下：
　　生2：1號(hào)陰影三角形的面積是左平行四邊形面積的一半，2號(hào)陰影三角形的面積是右平行四邊形面積的一半，所以陰影大三角形面積是平行四邊形面積的一半。
　　師：你能運(yùn)用前面所學(xué)的分割再求和的方法來解決面積問題，說明你很會(huì)學(xué)以致用。
　　生3：陰影三角形和平行四邊形的底相等，高也相等，三角形的面積=底×高÷2，所以陰影三角形的面積是平行四邊形面積的一半。
　　師：你的方法很有價(jià)值。
　　生4：我還可以畫很多與這個(gè)平行四邊形等底等高的三角形。
　　生4上黑板示范：
　　師：這些不同的三角形有什么相同之處？
　　生5：這些三角形等底等高，面積都相等。
　　生6：這些三角形與平行四邊形也是等底等高，面積都是平行四邊形面積的一半。
　　師：像這樣等底等高的三角形在這個(gè)平行四邊形中能畫多少個(gè)？
　　生（齊）：無數(shù)個(gè)。
　　接著出示書上的問題，學(xué)生解答。
　　在這個(gè)教學(xué)片段中，教師沒有直接讓學(xué)生解決書上的習(xí)題，而是拋出“三角形的面積和平行四邊形的面積有什么關(guān)系”這個(gè)問題，學(xué)生從更廣闊的空間中搜索已有經(jīng)驗(yàn)，思考的方法各不相同，使學(xué)生解決問題的能力得到提升，思維更開放、更自由、更廣闊。
　　二、合理選擇問題延伸方向，從“聚合”走向“發(fā)散”
　　培養(yǎng)學(xué)生的思維能力是數(shù)學(xué)教學(xué)追求的目標(biāo)之一。教材中的習(xí)題，通常關(guān)注的是一個(gè)狹窄的目標(biāo)，容易讓學(xué)生的思維集中在一個(gè)主題上，不利于數(shù)學(xué)思維的培養(yǎng)。這就需要在教學(xué)中，積極引導(dǎo)學(xué)生對(duì)問題進(jìn)行深入討論，把學(xué)生的思維“發(fā)散”，不斷提升學(xué)生的思維能力。
　　【案例2】 蘇教版四（下）《認(rèn)識(shí)三角形》
　　下面的三根小棒能圍成一個(gè)三角形嗎？為什么？
　　第一組：3厘米，4厘米，5厘米；
　　第二組：3厘米，3厘米，3厘米；
　　第三組：3厘米，3厘米，7厘米；
　　第四組：3厘米，3厘米，5厘米。
　　師：仔細(xì)觀察每組中的三個(gè)數(shù)據(jù)，同學(xué)們有沒有發(fā)現(xiàn)什么？先來看看第一小題。
　　生：這三根小棒的長(zhǎng)度是三個(gè)連續(xù)的自然數(shù)。
　　師：是不是三根小棒的長(zhǎng)度是三個(gè)連續(xù)的自然數(shù)，就一定能圍成一個(gè)三角形呢？
　　生：是的，比如4厘米、5厘米和6厘米。
　　生：不對(duì)，如果是1厘米、2厘米和3厘米，就不行了。
　　師：那么怎樣說才對(duì)呢？
　　……
　　師：再來看第二組三根小棒的長(zhǎng)度，你又發(fā)現(xiàn)了什么？由此，你又有什么新猜想？
　　生：我發(fā)現(xiàn)這三根小棒的長(zhǎng)度完全相等。我猜想是不是三根長(zhǎng)度完全相等的小棒都能圍成一個(gè)三角形？
　　師：他的猜想對(duì)嗎？誰來說說你的看法。
　　……
　　師：再來看第三組，同學(xué)們能不能變換其中的一個(gè)數(shù)據(jù)，使它能圍成一個(gè)三角形？
　　……
　　上述教學(xué)片段，教師沒有止步于書上的問題，而是對(duì)問題進(jìn)行了延伸拓展，引領(lǐng)學(xué)生嘗試著透過數(shù)字這一表面現(xiàn)象，找尋和發(fā)現(xiàn)其背后的規(guī)律，對(duì)能圍成三角形的三根小棒的長(zhǎng)度問題有了更深層次的理解與把握。
　　三、適時(shí)抓住生成性資源，從“意外”走向“精彩”
　　“課堂應(yīng)是向未知方向挺進(jìn)的旅行，隨時(shí)都有可能發(fā)現(xiàn)意外的通道和美麗的圖景，而不是一切都必須遵循固定路線而沒有激情的行程。”（葉瀾語）學(xué)生在解題時(shí)思維旁逸斜出，經(jīng)常會(huì)有一些意外生成的資源，教師要抓住學(xué)生思維的細(xì)節(jié)，引導(dǎo)學(xué)生正確地理解數(shù)學(xué)與生活的關(guān)系。
　　【案例3】 蘇教版五（上）第62頁(yè)
　　1.我國(guó)民間通常用下面12種動(dòng)物（十二生肖）來表示不同的出生年份。
　　師：從今年起再過多少年又是豬年呢？（那一年正好是豬年）
　　生1：再過12年。
　　生2：再過24年好像也是豬年。
　　生3：只要是12的倍數(shù)都可以的。
　　師：思考逐步深入，真棒，那是為什么呢？
　　生：十二個(gè)動(dòng)物分別代表十二年一組一直重復(fù)下去的。
　　師：很好，那你們是屬牛的，比你們大多少歲的人和你的屬相一樣呢？
　　生1：12歲，24歲……
　　生2：這里只要是12倍數(shù)的歲數(shù)也都可以的。
　　（將錯(cuò)就錯(cuò)，繼續(xù)追問）
　　師：那240歲也是12的倍數(shù)，可以嗎？
　　生：不行的，人的歲數(shù)是有限的。
　　師：老師今年是30歲，屬蛇，我的兒子也是屬蛇，他今年可能是多少歲呢？
　　生1：18歲。
　　生2：6歲。
　　師：是嗎？有不同意見嗎？
　　生：我不同意，如果是18歲的話，劉老師12歲就結(jié)婚了，那不可能！
　　（這時(shí)，許多學(xué)生恍然大悟。）
　　師：說得好極了，看來，咱們解決數(shù)學(xué)問題還要從實(shí)際情況出發(fā)！
　　……
　　“動(dòng)態(tài)生成”追求的是教學(xué)的真實(shí)自然，敢于“暴露”意料之外的情況。在數(shù)學(xué)習(xí)題教學(xué)中我們要及時(shí)捕捉學(xué)生出現(xiàn)的生成資源，巧妙地挖掘數(shù)學(xué)思考的問題所在，把習(xí)題解決的過程化為一次新的學(xué)習(xí)，讓習(xí)題變?yōu)椤昂玫摹⒂袃r(jià)值的問題”，使每一位學(xué)生“像野花一樣自然成長(zhǎng)”！
　　（責(zé)編　金