一道思考題引出的精彩

　　在一節數學活動課上，我出示了下面的思考題：圖1是用邊長為1厘米的小正方形圍成的圖形，你能算出這個圖形的周長是多少厘米嗎？
　　全班學生冥思苦想，一時得不到答案。我本想引導學生一起分析這個圖形的周長是指圖中哪一部分，怎樣才能算出這個圖形的周長。后來轉念一想，不如把探索問題的過程交給學生。
　　師：你能用學具盒里面1厘米的小棒在小組里擺一擺嗎？
　　學生分小組活動。不一會兒有幾個學生舉起了手。
　　生1：根據周長的意義，把圍成圖形的所有邊長加起來，得2+1+1+2+1+1+2+4=14厘米。
　　師：同意嗎？
　　大多數同學點頭同意。
　　生2：我們可以數圍成圖形的周長里面有幾條1厘米的線段。一共有14條1厘米的線段，就用1×14=14厘米。
　　師：你能在小組里數一數嗎？
　　學生在小組里互相數一數。
　　生3：如果小正方形的數目多，數起來就很麻煩。
　　師：看起來你還有更好的方法！
　　生3：我們也可以這樣計算，這個圖形是由6個小正方形組成的，每個正方形有4條邊，一共有24條邊，就是1×24=24厘米，在圖形里面共有5組邊重復，每組邊是由相鄰的兩個正方形的兩條邊組成的，要減去10條邊的長，就是要減去1×10=10厘米，然后得24-10=14厘米。
　　師：你的意思是先計算出6個正方形的總邊長，然后減去圖形里所有重復邊的長度，就是這個圖形的周長。
　　生3：對。
　　師：你們還能用其他方法來求這個圖形的周長嗎？
　　生4：用前面學過的平移方法計算這個圖形的周長。
　　看到學生這么活躍，我索性順水推舟，讓學生動手用小棒移一移。
　　師：你能在小組里用小棒移一移嗎？
　　生5：不好平移，把凹進去的一條較長的線段移上去的話，得到了一個長方形c48Ryec1+n/BsEsF4G1gVfOfApU9AmCB3xNLwQJYckw=，但這個長方形的周長不等于這個圖形的周長（如圖2）。
　　師：怎么辦呢？用上面平移的方法能不能計算出這個圖形的周長呢？小組里面討論一下！
　　生6：把凹進去較長的的線段平移上去以后，就少算了兩條較短的邊，計算圖形的周長，如果用長方形的周長那還要加上少算了的兩條邊的長，得4+2=6厘米，6×2=12厘米，12+2=14厘米。
　　至此，學生一共得出了四種方法，教學目標基本達成，我本想小結一下，進入下一個環節的教學，突然有一個學生舉起了小手。
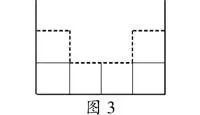
　　生7：我還可以把凹進去的兩條較短的線段移到寬上，里面的3條線段移到長上（如圖3）。這樣，就把這個圖形轉化成規則的長方形，這個長方形的長是4厘米，寬是2+1=3厘米，得4+3=7厘米，7×2=14厘米。
　　全班同學響起了熱烈的掌聲！
　　【反思】我們平時的課堂，大都按照預定的設計進行教學，一節課的教學活動非常緊湊，課堂容量非常大。但本節課中我改變了原先的設計，先讓學生利用學具盒里面的1厘米的小棒在小組里擺一擺，竟收到意想不到的效果，學生很快發現了三種解法，此時我并沒有就此收場，而是繼續提問學生：“你還能用其他方法來求這個圖形的周長嗎？”當有學生想到可以用前面學過的平移方法時，我順水推舟讓學生在小組里移一移，使得學生的思維步步深入，后面的精彩才如期而至。
　　可以設想一下，這一節課如果按原先的設計，循規蹈矩，學生就會被老師牽著鼻子走，他們的積極性就會受到影響，思維就會被禁錮起來，就不能用原來的知識去順應新的知識。在教學中，我們面對是不同的學生，他們的真實水平往往無法準確估計。在實施具體教學的過程中，教師要根據教學的具體情況冷靜思考，靈活地調整教學方法，機智生成新的教學方案。數學課堂的動態生成離不開教師的預設，教師的設計不能過于精細，教師的預設要著眼于整體、著眼于開放，同時教師的預設要富有彈性，要給學生留足空間，為學生搭建個性張揚的舞臺，激活學生心中那小小的“漣漪”，激起學生在課堂上的“千層浪”，引發思維碰撞的“共鳴”，真正煥發出生態課堂的活力。
　　其次，這節課我讓學生動手擺一擺、移一移，這不僅符合學生好奇、好動的心理特點和幾何初步知識直觀、操作性強的知識特點，更重要的是充分體現了以活動促發展的教學思想。整個教學過程是以學習者為中心，以學生的自主活動為基礎，使學生在活動中學習，在活動中探索，在活動中發展，學生真正動了起來，課堂真正活了起來。因此在教學中我們要向學生充分提供從事數學活動的機會，幫助他們在自主探索、合作交流的過程中真正理解和掌握基本的數學知識與技能、數學思想和方法，獲得廣泛的數學活動經驗，使學生真正成為學習的主人。
　　（責編　金