基于Lingo后勤運輸優化模型研究
2012-12-31 00:00:00祁波鄭磊武愷航
群文天地 2012年16期
摘要:本文結合數學建模和軟件求解的方法,建立了平時情況下的后勤運輸優化模型,并給出了模型的通用解法。通過對實例的分析和求解,說明了該模型的有效性和通用性。
關鍵字:后勤運輸;優化;LINGO
后勤運輸問題是伴隨后勤保障問題而產生的,是資源在特定約束條件下的分配問題。本文擬通過數學建模的方法對平時后勤運輸問題建立優化模型,以假設的一后勤運輸問題為背景,通過建立數學模型和編寫LINGO程序對這類問題進行求解。
一、問題背景
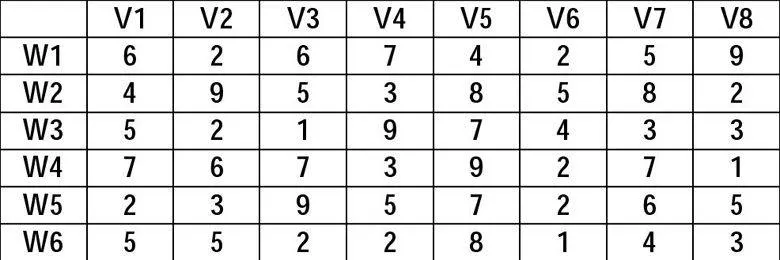
某后勤部門下屬有6個物資倉庫存儲有某種通用物資,各倉庫庫存某物資數量分別為60,55,51,43,41,52箱,現有8個單位請領這一物資,數量分別為35,37,22,32,41,32,43,38。現聯勤部門準備給8個缺少這批物資的單位發送所請領的物資,將其運至各場站附近車站等地,由請領單位派人領取運回。由于天氣原因,需要在規定時間內完成對所有請領物資的發放。各倉庫到各請領單位附近車站的單位物資運輸耗費見下表:
倉庫至車站單位物資耗費表
由上表,制定計劃的參謀通過拼湊可找出一可行解,以下即為一可行解:即:W1、W2分別向V1運送19、16個單位的物資;W2向V2運送37個單位的物資;W3向V3運送22個單位的物資;W4向V4運送32個單位的物資;W1向V5運送41個單位的物資;W3、W6分別向V7運送23、20個單位的物資;W2、W4、W5分別向V8運送18、9、11個單位的物資。基于這一可行解的總費用為:
Z=6×19+4×16+37×9+22×1+32×3+41×4+32×1+23×3+20×4+9×1+18×2+11×5=1154
現在的問題在于這一可行解是不是最優解,怎樣才能找到最優解,即花費最小完成任務。為此需要通過建立數學模型來進行求解。
二、問題假設
1、每個保障單位對物資的時間較充裕。2、單位里程的消耗是均勻的。
三、符號約定
xij:從第i個倉庫到第j個車站的物資運量。cij:從第i個倉庫到第j個車站的單位物資運輸費用。
ai:從第i個倉庫的物資儲量。dj:從第j個場站的請領量。
四、模型建立
引入決策變量xij,代表從第i個倉庫到第j個車站的物資運量,用cij表示從第i個倉庫到第j個車站的單位物資運價,aij表示從第i個倉庫的物資儲量,dij表示從第j個場站的請領量。
五、模型求解
對于線性規劃問題,一般使用LINGO軟件求解,LINGO是專門用來求解各種規劃問題軟件包,其功能十分強大。是求解優化模型的最佳選擇。以下為LINGO求解的過程。
1.集合定義部分。先定義倉庫集合: CK/K1...K6/:ZL;其中CK是集合的名稱,K1...K6是集合內的成員,“..”是特定的省略號,表明該集合有6個元素,對應六個倉庫,ZL是集合的屬性,表示倉庫的物資總量。
同理,定義車站集合, CZ/Z1..Z2/:QL;為了表示數學模型中的運輸關系以及與此相關的運輸單價和運量,在定義一個表示運輸關系的集合 LINKS(CK,CZ):C,X;該集合是以CK和CZ為基礎產生的衍生集合(或稱派生集合)。C,X為衍生集合的兩個屬性,分別表示到相應車站的單位貨運價和從某倉庫的到某車站的貨運總量。
2.數據初始化。定義的集合中,X(有48個元素)是決策變量,是待求系數,屬性ZL、QL和C的元素已知。數據初始化只需在程序中按語法輸入即可。
3.目標函數和約束條件。目標函數表達式的LINGO程序為:MIN=@SUM(LINKS(I,J):C(I,J)*X(I,J));式中, @SUM是求和函數,第一個參數LINKS(I,J),表示求和函數是對衍生集合進行;第二個參數為表達式C(I,J)*X(I,J)。
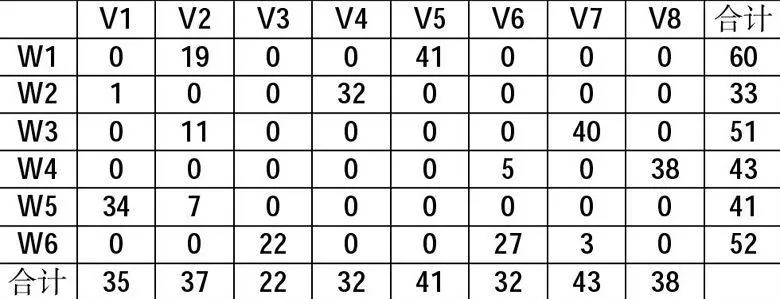
4.運算結果。通過編程計算,結果表明:目標函數值為664,即最省的方案下總費用為664.最優運輸方案如下,該方案下完成任務花費的費用最省。
六、 結束語
后勤運輸優化是一個大規模的線性規劃問題,本文考慮到篇幅限制假設背景只是少數倉庫對少數保障單位的情況,實際情況往往比這復雜的多。本文建立的數學模型和求解方法適用于后勤運輸的大部分情況,在求解的過程中,只需改變初始的矩陣即可,具有較強的通用性,Lingo是解決規劃問題專業軟件,與其他大型的數學軟件相比較,LINGO在線性規劃,整數規劃,0-1規劃以及圖論和網絡模型的求解方面多具有很多的優勢,可以考慮基于Lingo開發相關的后勤運輸優化軟件。將對后勤運輸效能的提高具有一定的促進作用。
(作者單位:空軍勤務學

