發(fā)電廠不同機(jī)組間各班組小指標(biāo)排名方法探討
閆海行
(大唐魯北發(fā)電有限責(zé)任公司 發(fā)電部,山東 濱州 251909)
發(fā)電廠不同機(jī)組間各班組小指標(biāo)排名方法探討
閆海行
(大唐魯北發(fā)電有限責(zé)任公司 發(fā)電部,山東 濱州 251909)
指標(biāo)競(jìng)賽是發(fā)電廠集控運(yùn)作工作中的一項(xiàng)重點(diǎn)工作,小指標(biāo)是一臺(tái)機(jī)組整體性能的體現(xiàn),也是運(yùn)行人員操作水平的體現(xiàn),同樣是績(jī)效考核管理系統(tǒng)的重要組成部分。由于發(fā)電廠不同機(jī)組間設(shè)備性能的差異,小指標(biāo)得分不盡相同,甚至有很大差異,由于操作水平的不同,同臺(tái)組不同班組間小指標(biāo)得分也有較大差異。原則上講,不同機(jī)組間的小指標(biāo)得分是沒(méi)有可比性的,但是有些時(shí)候需要把所有班組放到一起綜合比較,這就給每個(gè)班組的指標(biāo)得分排名帶來(lái)了困難。本文在指標(biāo)修正上提出了幾種算法,試圖尋找一種更為合理的辦法,使不同機(jī)組間的小指標(biāo)得分排名更為公平。
發(fā)電廠;集控運(yùn)行;指標(biāo)競(jìng)賽;績(jī)效得分;指標(biāo)修正;平均數(shù);方差
0 前言
大唐魯北發(fā)電有限責(zé)任公司成立于2009年3月25日,建設(shè)有兩臺(tái)330MW燃煤熱電聯(lián)產(chǎn)機(jī)組,分別于2009年9月21日和12月20日投產(chǎn)發(fā)電。指標(biāo)競(jìng)賽是發(fā)電廠集控運(yùn)行工作中的一項(xiàng)重點(diǎn)工作,由于兩臺(tái)機(jī)組設(shè)備性能的差異,造成績(jī)效得分有所不同,1、2號(hào)機(jī)在整體上有很大差異,而且每個(gè)班組由于運(yùn)行人員操作水平或設(shè)備運(yùn)行狀況的不同,績(jī)效得分也有較大差異。因?yàn)榭?jī)效得分與個(gè)人獎(jiǎng)金分配和崗位晉升有很大關(guān)系,這就給兩臺(tái)機(jī)5個(gè)值相當(dāng)于10個(gè)班組的綜合評(píng)價(jià)帶來(lái)了困難。所以我們希望這個(gè)綜合評(píng)價(jià)越合理、越公平越好,下文將就這個(gè)問(wèn)題展開(kāi)論述,尋找一種計(jì)算方法,使每個(gè)班組的排名更加科學(xué)合理。
1 平均數(shù)與方差的性質(zhì)
(1)如果一組數(shù)據(jù)x1,x2,……,xn的平均數(shù)為x,方差為s2,那么一組新數(shù)據(jù)ax1,ax2……,axn的平均數(shù)為ax,方差是a2s2.
(2)如果數(shù)據(jù)x1,x2,……,xn的平均數(shù)為x,方差為s2,那么一組新數(shù)據(jù)x1+b,x2+b,……xn+b的平均數(shù)為x+b,方差是s2.
(3)如果數(shù)據(jù)x1,x2,……,xn的平均數(shù)為 x,方差為s2,那么一組新數(shù)據(jù)ax1+b,ax2+b,……,axn+b的平均數(shù)為ax+b,方差是a2s2.
2 指標(biāo)修正
不同機(jī)組間的小指標(biāo)得分差距很大,顯然把每個(gè)班組實(shí)際的得分放到一起排名是不合理的,我們一般采取的辦法是將一臺(tái)機(jī)組的小指標(biāo)得分修正一下再和另一臺(tái)機(jī)組做比較,修正的原則是使兩臺(tái)機(jī)的平均得分相同,也就是每臺(tái)機(jī)的總分相同。
以2013年4月份大唐魯北發(fā)電廠兩臺(tái)機(jī)組的小指標(biāo)得分為例:
1號(hào)機(jī)指標(biāo)得分:一值16.18,二值14.14,三值14.25,四值16.82,五值15.83,平均得分15.45,方差1.14。
2號(hào)機(jī)指標(biāo)得分:一值23.09,二值21.93,三值21.74,四值21.08,五值22.72,平均得分22.11,方差0.51。
兩臺(tái)機(jī)組的得分相差很大,顯然直接給這10個(gè)數(shù)據(jù)排名是不合理的,一般情況下,我們把分?jǐn)?shù)較少的1號(hào)機(jī)平均得分提高,使兩臺(tái)機(jī)組平均得分相同。我們將1號(hào)機(jī)和2號(hào)機(jī)指標(biāo)得分命名為數(shù)組1和數(shù)組2。
2.1 算法一
計(jì)算兩組數(shù)據(jù)平均數(shù)的倍數(shù)為1.432。即將1號(hào)機(jī)的指標(biāo)得分乘以1.432,假設(shè)1號(hào)機(jī)原指標(biāo)為x,修正指標(biāo)為y,那么y=1.432x,可獲得1號(hào)機(jī)五個(gè)值的修正指標(biāo):一值23.17,二值20.24,三值20.40,四值24.08,五值22.66。這五組數(shù)的方差是2.34。
2.2 算法二
計(jì)算兩組數(shù)據(jù)平均數(shù)的差為6.67。即將1號(hào)機(jī)的指標(biāo)得分加上6.67。假設(shè)1號(hào)機(jī)原指標(biāo)為x,修正指標(biāo)為y,那么y=x+6.67,可獲得1號(hào)機(jī)五個(gè)值的修正指標(biāo):一值22.85,二值20.81,三值20.92,四值23.48,五值22.5。這五組數(shù)的方差是1.14。
2.3 算法三
按照上面的性質(zhì) 3,已知1號(hào)機(jī)原數(shù)據(jù)平均數(shù)x=15.45,方差s2=1.14,求一組新數(shù)據(jù)y使y=ax+b,滿足下列方程式:
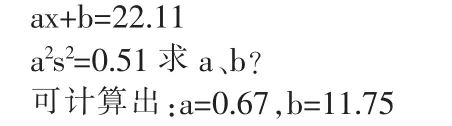
于是可獲得1號(hào)機(jī)五個(gè)值的修正指標(biāo):一值22.61,二值21.24,三值21.31,四值23.03,五值22.37。這五組數(shù)的方差是0.51。
3 算法分析
第一種算法獲得的數(shù)據(jù)方差為2.34,比原始數(shù)據(jù)的方差大了1.2,第二種算法獲得的數(shù)據(jù)方差是1.14,與原始數(shù)據(jù)方差相同。這就是說(shuō)第一種算法把1號(hào)機(jī)五個(gè)值之間的相對(duì)得分差距拉大了,使得分高的班組修正得分相對(duì)更高,得分低的班組修正得分相對(duì)更低。第二種算法縮小了第一名與第五名的得分差但卻保持了原來(lái)的相對(duì)得分差距。因此算法二要優(yōu)于算法一,它的波動(dòng)性更小,數(shù)據(jù)更向平均數(shù)靠攏,在1號(hào)機(jī)五個(gè)班組間是相對(duì)公平的。
2號(hào)機(jī)各班組的得分?jǐn)?shù)據(jù)方差是0.51,說(shuō)明2號(hào)機(jī)運(yùn)行人員水平更加平均,或者設(shè)備運(yùn)行情況更加穩(wěn)定。1號(hào)機(jī)經(jīng)過(guò)修正后的數(shù)據(jù)方差后依然是1.14,遠(yuǎn)大于0.51,這說(shuō)明1號(hào)機(jī)運(yùn)行人員調(diào)整水平差距過(guò)大或者設(shè)備運(yùn)行情況不穩(wěn)定,過(guò)高的平均分差加在1號(hào)機(jī)數(shù)據(jù)上后,使1號(hào)機(jī)得分高的班組遠(yuǎn)大于2號(hào)機(jī)各班組,得分低的班組遠(yuǎn)低于2號(hào)機(jī)各班組,采取第一種算法甚至?xí)惯@個(gè)差距更大,這對(duì)2號(hào)機(jī)的各班組是不公平的。因此某臺(tái)機(jī)組過(guò)高的得分差距會(huì)使前兩種算法獲得的修正數(shù)據(jù)對(duì)某些班組產(chǎn)生不公平。
產(chǎn)生這種現(xiàn)象的原因是修正后的1、2號(hào)機(jī)數(shù)據(jù)雖然有著相同的平均數(shù),但方差不同。算法三就是使修正后的1號(hào)機(jī)數(shù)據(jù)與2號(hào)機(jī)數(shù)據(jù)既有著相同的平均數(shù)又有著相等的方差。將1號(hào)機(jī)修正后的三組數(shù)據(jù)和2號(hào)機(jī)的數(shù)據(jù)放到一組曲線中如下圖所示:
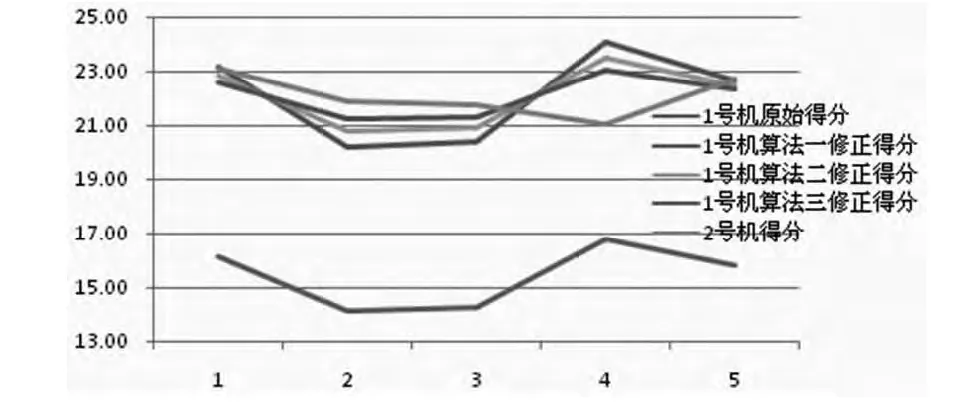
可以看出,算法三獲得的修正數(shù)據(jù)相對(duì)算法一、二更為集中穩(wěn)定,這種算法相對(duì)更加合理。
4 結(jié)論
沒(méi)有絕對(duì)的公平,只有相對(duì)的合理。上述三種算法所得的得分差距很小,實(shí)際上,由于機(jī)組不同,根本沒(méi)有一種完全公平的算法來(lái)解決這個(gè)問(wèn)題。以上三種算法是以得分較高的2號(hào)機(jī)為基準(zhǔn)的,如果取全年12個(gè)月的指標(biāo)得分做比較,未必每個(gè)月都是2號(hào)機(jī)得分高或者方差小,如果1號(hào)機(jī)的得分方差小,也可以1號(hào)機(jī)為標(biāo)準(zhǔn)來(lái)修正2號(hào)機(jī)指標(biāo),而且這也是一種更為合理的做法。本文認(rèn)為只要是兩臺(tái)機(jī)的得分?jǐn)?shù)據(jù)平均數(shù)相同,方差相等,就是一種相對(duì)合理的比較。本文的算法同樣適合多臺(tái)發(fā)電機(jī)組間各個(gè)班組間的指標(biāo)排名比較。
[1]宗序平.概率論與數(shù)理統(tǒng)計(jì)[M].2011-5-1.
湯靜]

