預(yù)應(yīng)力超高強(qiáng)混凝土梁抗彎性能試驗研究＊

孟 剛 賈金青 劉春梅

（大連理工大學(xué)港口和近海工程國家重點實驗室1） 大連 116024） （大連科諾科技發(fā)展有限公司2） 大連 116023）

0 引 言

超高強(qiáng)混凝土具有比強(qiáng)度高、負(fù)荷能力大、資源和能源消耗少、耐久性優(yōu)異、可有效控制構(gòu)件截面尺寸等特點［1］，特別適用于大跨、重載、高層和超高層結(jié)構(gòu)中，隨著超高強(qiáng)混凝土配置技術(shù)和施工泵送技術(shù)日益成熟，C100級超高強(qiáng)混凝土已逐漸應(yīng)用于工程中［2］．但我國新修訂的規(guī)范《混凝土結(jié)構(gòu)設(shè)計規(guī)范》（GB50010－2010）［3］以及《公路鋼筋混凝土及預(yù)應(yīng)力混凝土橋涵設(shè)計規(guī)范》（JTG D62－20040）［4］僅適用的混凝土強(qiáng)度等級為C15～C80，明顯滯后于超高混凝土結(jié)構(gòu)在實際工程中的應(yīng)用，因此對超高強(qiáng)混凝土結(jié)構(gòu)體系進(jìn)行系統(tǒng)的研究是十分必要的．目前國內(nèi)外對超高強(qiáng)混凝土柱、節(jié)點的受力性能研究較多［5－6］，但對超高強(qiáng)混凝土受彎構(gòu)件的受力性能研究較少．本文以預(yù)應(yīng)力筋位置和預(yù)應(yīng)力筋配筋率為主要研究因素對預(yù)應(yīng)力超高強(qiáng)混凝土簡支梁進(jìn)行了靜力荷載下的抗彎性能試驗，并通過有限元程序ANSYS對其進(jìn)行了承載力數(shù)值模擬計算，并與試驗結(jié)果進(jìn)行比較．

1 試件設(shè)計和試驗方案

1．1 試件設(shè)計

試驗共對4根后張法預(yù)應(yīng)力超高強(qiáng)混凝土簡支梁進(jìn)行張拉階段的受力監(jiān)測，梁長為4．0m，跨度為3．7m，截面尺寸為200mm×300mm，普通縱向受力鋼筋采用HRB335級鋼筋，箍筋為HPB235級鋼筋，預(yù)應(yīng)力筋采用1 860級高效低松弛鋼絞線，張拉控制應(yīng)力均為0．70fpfk（fptk為預(yù)應(yīng)力筋抗拉強(qiáng)度標(biāo)準(zhǔn)值），預(yù)應(yīng)力錨具采用低回縮錨具．試件梁的縱筋配筋均為AS＝3B18，A′S＝3B14，箍筋的配筋滿足構(gòu)造配筋，保證試件梁的彎曲破壞，支座處φ8＠50，剪跨段φ8＠150，純彎段φ8＠200．試驗梁配筋見圖1～2，預(yù)應(yīng)力筋配筋情況見表1．

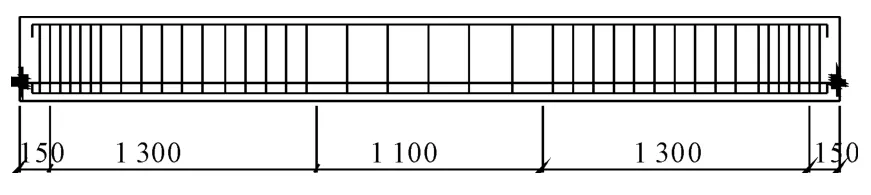
圖1 試驗梁配筋示意圖（單位：mm）

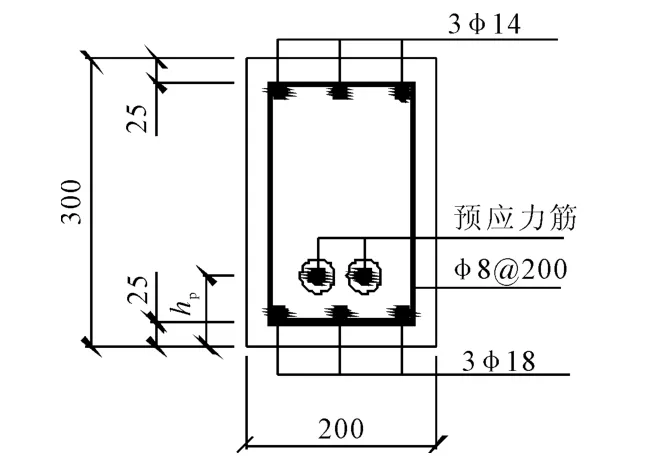
圖2 試驗梁的截面示意圖（單位：mm）

表1 試驗梁預(yù)應(yīng)力筋的設(shè)計參數(shù)

1．2 材料性能

試驗梁超高強(qiáng)混凝土標(biāo)準(zhǔn)立方體抗壓強(qiáng)度平均值fcu＝102．5MPa，標(biāo)準(zhǔn)棱柱體抗壓強(qiáng)度平均值fc＝86．18MPa，彈性模量Ec＝38．7MPa，鋼筋及鋼絞線的屈服強(qiáng)度fy、極限強(qiáng)度fu及彈性模量實測值見表2．

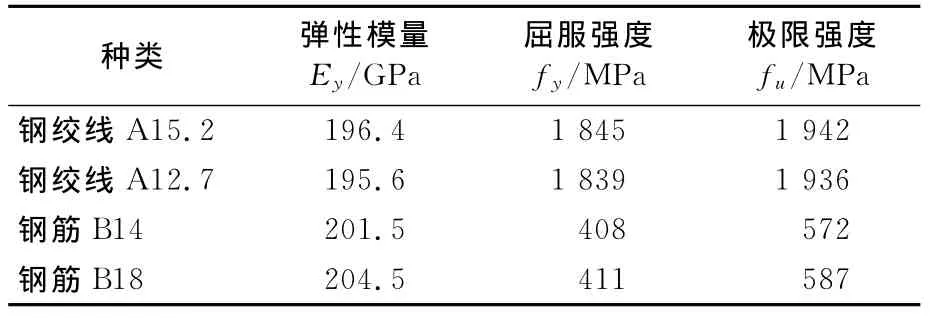
表2 鋼絞線及鋼筋實測力學(xué)性能指標(biāo)

1．3 試驗方案

試驗均采用2點集中對稱的同步分級加載方式．首先對試件進(jìn)行預(yù)加載，調(diào)試儀器，然后卸載，將傳感器、應(yīng)變片和位移計調(diào)零；在試件開裂前，每級所加荷載約為0．05 Mu（Mu為跨中極限彎矩），持載10min；試件開裂后每級所加荷載約為0．1 Mu，持載10min；試件達(dá)到屈服荷載后加載幅度恢復(fù)至0．05 Mu，直至試件達(dá)到極限荷載破壞．荷載由10 000kN試驗機(jī)在分配梁上施加，并通過荷載傳感器測量施加荷載的大小；跨中梁底設(shè)置位移傳感器測量試件的撓度；沿試件跨中截面高度方向布置混凝土應(yīng)變片以及純彎段縱筋、鋼絞線表面布置應(yīng)變片；荷載、位移傳感器和應(yīng)變片數(shù)據(jù)通過IMC系統(tǒng)自動采集，跨中純彎段長度為1 100mm，試驗加載方式見圖3．

2 試驗現(xiàn)象與試驗結(jié)果分析

2．1 試驗現(xiàn)象

圖3 試驗梁加載圖

在加載初期，試驗梁的荷載撓度曲線基本呈線性變化，當(dāng)荷載達(dá)到0．3 Mu（彎矩為50kN·m）左右時，首先在試驗梁純彎段下邊緣出現(xiàn)豎向彎曲微裂縫；隨著荷載的增加，由于鋼筋和混凝土的粘結(jié)與應(yīng)力傳遞，裂縫數(shù)量增加，裂縫間距均勻，一般9～11mm之間；當(dāng)荷載達(dá)到0．6 Mu（彎矩為105kN·m）左右時，純彎段新裂縫基本不出現(xiàn)，原有裂縫寬度擴(kuò)展并向上延伸；當(dāng)荷載達(dá)到0．75 Mu（彎矩為130kN·m）左右時，剪跨段出現(xiàn)多條裂縫，間距均勻，并由梁下邊緣向加載點傾斜延伸，純彎段裂縫繼續(xù)向上延伸擴(kuò)展，跨中最大裂縫寬度0．2mm；荷載繼續(xù)增加，達(dá)到0．85 Mu（即彎矩為148kN·m）左右時，試驗梁屈服，受壓區(qū)混凝土壓裂，并伴隨有混凝土崩裂聲音，新裂縫不再出現(xiàn)，純彎段裂縫繼續(xù)向上擴(kuò)展，剪跨段裂縫繼續(xù)向加載點傾斜擴(kuò)展，最大裂縫寬度0．68mm．當(dāng)荷載臨近極限彎矩Mu時，裂縫發(fā)展加快，跨中撓度增加迅速，純彎段受壓區(qū)混凝土在受壓筋位置附近出現(xiàn)水平裂縫，最終受壓區(qū)混凝土壓碎，梁達(dá)到極限狀態(tài)，試驗梁均呈現(xiàn)彎曲破壞形態(tài)．由于超高強(qiáng)混凝土脆性大，試驗梁達(dá)到極限承載力后，承載力迅速降低．試件梁破壞形態(tài)見圖4．

圖4 試驗梁彎曲破壞形式及裂縫分布情況

2．2 試驗結(jié)果分析

2．2．1 荷載－撓度曲線

圖5為各試驗梁跨中截面荷載－撓度曲線．由圖5可見，荷載達(dá)到極限荷載的30%之前，跨中截面的撓度基本呈線性增長趨勢，試驗梁處于彈性階段；隨后曲線出現(xiàn)第一個拐點，在極限荷載的30%～85%之間，撓度增長速度加快，試驗梁進(jìn)入彈塑性階段；達(dá)到極限荷載的85%以后，荷載增加變緩，撓度迅速增張，受拉縱筋屈服，試驗梁進(jìn)入屈服階段，屈服點較為明顯；達(dá)到極限荷載后，承載力迅速降低，撓度增長較緩．試驗梁中均配置了一定數(shù)量的受壓縱筋，在一定程度上改善超高強(qiáng)混凝土材料脆性破壞特點，使得荷載－撓度曲線達(dá)到極限荷載之后位移略有增加，由此得出增大受壓縱筋的配筋率有利于改善超高強(qiáng)混凝土梁的脆性破壞情況．

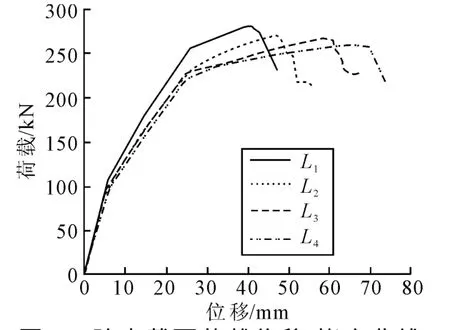
圖5 跨中截面荷載位移－撓度曲線

2．2．2 設(shè)計參數(shù)的影響

1）預(yù)應(yīng)力的施加能夠有效的控制構(gòu)件的開裂和撓度，試驗梁L1～L4屈服時最大裂縫寬度依次為0．48，0．6，0．68，0．52mm．由此得出，預(yù)應(yīng)力筋高度hp以及預(yù)應(yīng)力筋配筋率對裂縫開展有一定影響，hp越小，試件屈服時最大裂縫寬度越小，試件L1比試件L3減小29．4%；預(yù)應(yīng)力筋的配筋率越大，試件屈服時最大裂縫寬度越小，但對試件抗裂性影響不明顯．

2）對于超高強(qiáng)混凝土梁，預(yù)應(yīng)力筋高度hp越大，梁的屈服段越長，梁的延性越好；預(yù)應(yīng)力筋配筋率越大，梁的屈服段較短，梁的延性越差．

3）表3為試驗梁的開裂荷載、屈服荷載和極限荷載．由此可見，在相同的預(yù)應(yīng)力張拉應(yīng)力的情況下，試件L1～L3的預(yù)應(yīng)力筋高度hp越小，預(yù)應(yīng)力筋提供的反彎矩越大，試件的開裂荷載越大，試件進(jìn)入消壓狀態(tài)以后，計算正截面彎矩平衡時，預(yù)應(yīng)力筋提供的彎矩越大，屈服荷載和極限荷載就越大；相同預(yù)應(yīng)力筋高度條件下，預(yù)應(yīng)力筋配筋越大，試件中和軸高度越小，混凝土受壓區(qū)越小，試件的開裂荷載、屈服荷載和極限荷載越大．

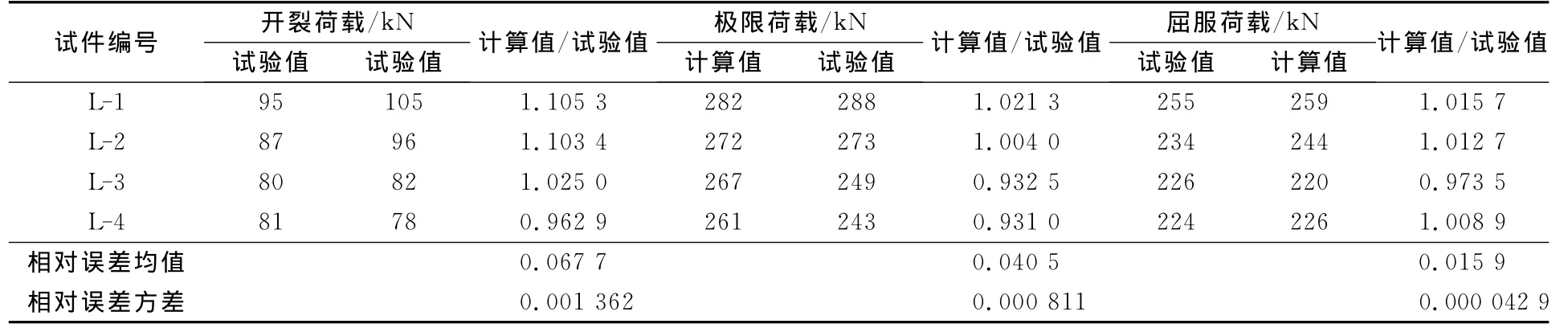
表3 試驗結(jié)果與計算結(jié)果對比

3 預(yù)應(yīng)力超高強(qiáng)混凝土梁承載力有限元計算分析

本文采用ANSYS有限元程序?qū)︻A(yù)應(yīng)力超高強(qiáng)混凝土梁在靜力荷載作用下的抗彎受力過程進(jìn)行數(shù)值模擬分析，采用蒲心誠［7］提出的超高強(qiáng)混凝土本構(gòu)模型，其單軸受壓情況下，不同強(qiáng)度等級的混凝土的應(yīng)力應(yīng)變上升段關(guān)系式為

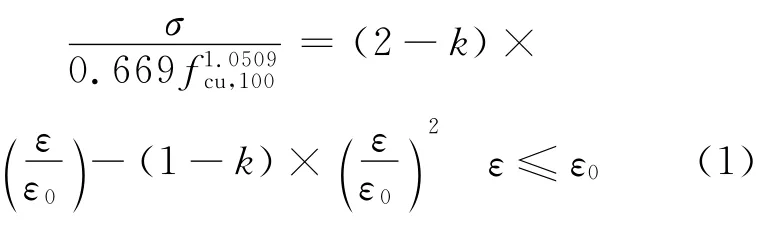
式中：fcu，100為試件尺寸為100mm×100mm×100mm的立方體抗壓強(qiáng)度；k為修正系數(shù)；ε0為峰值應(yīng)變．

修正系數(shù)k按k＝0．494 7infcu，100－1．577 1

峰值應(yīng) 變ε0＝ （8．505 5fcu，100＋123 0）×10－6

fcu，100和標(biāo)準(zhǔn)立方體試塊抗壓強(qiáng)度fcu之間的換算關(guān)系以及標(biāo)準(zhǔn)棱柱體試件軸心抗壓強(qiáng)度fc與標(biāo)準(zhǔn)立方體試塊抗壓強(qiáng)度fcu的換算關(guān)系為［7］

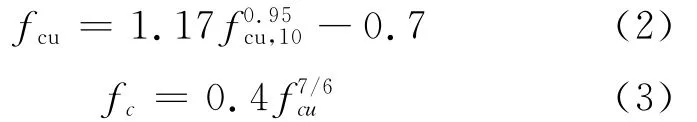
在ANSYS分析中，混凝土采用SOLID65單元進(jìn)行模擬，在計算中不考慮形函數(shù)的附加項，便于收斂．縱筋、箍筋以及預(yù)應(yīng)力筋采用空間二節(jié)點桿單元LINK8進(jìn)行模擬［8］．混凝土采用多線性隨動強(qiáng)化模型（KINH），破壞準(zhǔn)則采用默認(rèn)的 William－Warnker五參數(shù)破壞準(zhǔn)則［9］．鋼材（工字鋼、縱筋、箍筋以及預(yù)應(yīng)力筋）單軸應(yīng)力－應(yīng)變關(guān)系采用二折線理想彈塑性模型．支座鋼墊塊和錨具墊塊采用彈性模型，彈性模量取鋼材的10倍．ANSYS中鋼材強(qiáng)化模型采用雙線性隨動強(qiáng)化模型（KBIN）．

對4根試驗梁進(jìn)行ANSYS數(shù)值模擬，采用2點對稱位移加載，控制子布，控制計算精度，4根試驗梁均收斂良好．

4 結(jié) 論

1）超高強(qiáng)混凝土梁具有較高的承載力，由于超高強(qiáng)混凝土材料的脆性問題，導(dǎo)致極限荷載后持載能力較差．

2）在超高強(qiáng)混凝土梁中施加預(yù)應(yīng)力，較好的抑制了裂縫的開展，控制了裂縫的寬度，改善了超高強(qiáng)混凝土梁正常使用階段的使用性能．

3）預(yù)應(yīng)力筋高度hp和預(yù)應(yīng)力筋配筋率對超高強(qiáng)混凝土梁受力性能有較為顯著的影響，當(dāng)hp較大或者相同預(yù)應(yīng)力筋位置配筋率較小時，能夠使超高強(qiáng)混凝土梁保持較高的承載力的同時，延長超高強(qiáng)混凝土梁屈服階段，提高梁的延性性能，改善其受力性能．

4）本文采用ANSYS有限元程序?qū)︻A(yù)應(yīng)力超高強(qiáng)混凝土梁承載力進(jìn)行數(shù)值模擬計算，計算結(jié)果與試驗結(jié)果吻合較好，為預(yù)應(yīng)力超高強(qiáng)混凝土梁受力性能分析提供了一種較為準(zhǔn)確的數(shù)值計算方法．

［1］蒲心誠．超高強(qiáng)高性能混凝土［M］．重慶：重慶大學(xué)出版社，2004．

［2］JOSEF H，CLAUS G．Structural behavior of partially concrete encased composite sections with high strength concrete［J］．ASCE Conf．Proc，2006，186（33）：346－355．

［3］中交公路規(guī)劃設(shè)計院．JTG D62—2004公路鋼筋混凝土及預(yù)應(yīng)力混凝土橋涵設(shè)計規(guī)范［S］．北京：人民交通出版社，2004．

［4］中交公路規(guī)劃設(shè)計院．GB50010—2010混凝土結(jié)構(gòu)設(shè)計規(guī)范［S］．北京：人民交通出版社，2010．

［5］賈金青．鋼骨高強(qiáng)混凝土柱的力學(xué)性能［M］．大連：大連理工大學(xué)出版社，2006．

［6］YAN Changwang，WANG Haitao，MENG Gang．Seism ic performance of steel reinforced ultra highstrength concrete columns［J］．Journal of SinChuan University：Engineering Science Edition，2009，41（3）：216－222．

［7］張謝東，王勇威，蒲心誠，等．單軸壓力56．3～164．9 MPa混凝土的應(yīng)力－應(yīng)變關(guān)系［J］．建筑結(jié)構(gòu)學(xué)報，2005，26（1）：97－102．

［8］王文煒，李 果，韓武欽．FRP加固鋼筋混凝土梁非線性有限元分析［J］．武漢理工大學(xué)學(xué)報：交通科學(xué)與工程版，2007，31（2）：235－238．

［9］毛 偉，賈金青，余 芳．分離模型預(yù)應(yīng)力混凝土梁數(shù)值模擬［J］．鐵道建筑，2011（7）：17－19．