考慮多間隙的齒輪柔性轉子耦合系統非線性動力學分析

崔 立，宋曉光，鄭建榮

(華東理工大學 機械與動力工程學院，上海 200237)

齒輪軸承轉子系統是在各種機械設備中都有廣泛的應用，由于現代機械傳動設備的要求越來越高，工作環境也開始向高速、高溫、重載方向發展，對于齒輪轉子系統的研究也就變得越來越重要。

目前對于齒輪非線性動力學進行了大量的研究，但是在齒輪軸承轉子耦合系統方面的研究還不夠成熟［1］。傳統的研究方法往往忽略了整個系統的耦合作用，考慮自由度較少，將軸和軸承當做剛性體處理，未考慮柔性轉子造成的響應或是將支承軸承簡化成線性力，未考慮非線性軸承力的影響。如Kahraman等［2］考慮時變嚙合剛度和齒側間隙，建立了齒輪系統的動力學模型，但僅考慮3個自由度。李潤方等［3］建立了彎扭耦合的齒輪系統力學數學模型，采用集中質量法，將支撐剛度設為定值，但未考慮軸、軸承對整個系統的影響。張鎖懷等［4］建立了具有齒側間隙的齒輪系統動力學模型，但轉軸為剛性軸，系統僅考慮4個自由度。也有研究考慮系統多個自由度，考慮齒輪嚙合產生的彎曲和扭轉耦合振動，但往往忽略系統中的多種非線性因素及柔性轉軸的影響［5-6］。

最近的研究開始考慮多種非線性因素耦合效應建模，比如Cai等［7-8］在建立齒輪軸承系統數學模型時，考慮了系統的強非線性因素，引入了非線性油膜力、非線性嚙合力，這種模型得到了軸承、主動輪、被動輪中心點的振動響應時異步的。Byrtus［9］使用模態綜合法建立了齒輪系統動力學模型，將時變嚙合剛度、齒側間隙、非線性軸承力等因素引入系統模型中，但未研究柔性轉軸的影響。崔亞輝等［10-11］在建立齒輪模型過程中，考慮齒側間隙、時變嚙合剛度、靜態傳動誤差、不平衡質量的影響。陳思雨等［12］建立了考慮齒側間隙、時變嚙合剛度齒輪模型，研究了齒輪非線性沖擊響應，對脫齒現象進行了研究。李明等［13］研究了齒輪轉子軸承系統的彎扭耦合振動和非線性動力學進展情況，提出應考慮多種激勵同時作用下系統的動力學分析、同時考慮多種非線性因素的齒輪轉子軸承系統動力學分析。蔣慶磊等［14］研究了齒輪傳動多轉子耦合系統振動特性，得到了齒輪副耦合作用對機組振動特性的影響。竇唯等［15］建立了高速齒輪轉子系統彎扭耦合振動模型，研究了偏心距、齒輪嚙合剛度等參數對系統振動響應的影響規律。但以上研究均未考慮滾動軸承的非線性振動影響。滾動軸承徑向間隙引起的非線性現象也可導致轉子系統失穩或進入混沌運動［16-17］。齒輪軸承轉子系統是一個多自由度、多耦合、多間隙的非線性振動問題，需要考慮齒側間隙、軸承徑向間隙等多間隙的非線性因素。

本文考慮齒側間隙、軸承徑向間隙，考慮齒輪時變嚙合剛度、軸承時變剛度，建立適用于復雜載荷的齒輪軸承柔性轉子耦合的動力學模型，研究轉速變化對齒輪系統動力學響應的影響、轉軸剛度變化對系統動態特性的影響規律、齒側間隙和軸承徑向間隙變化對系統混沌運動的影響，提高齒輪轉子系統的可靠性。

1 計算模型

首先建立齒輪副嚙合模型和動力學模型;然后推導滾動軸承接觸力的非線性模型;接著采用有限單元法將轉子系統劃分為彈性軸段、圓盤及支承，建立各節點的動力學模型;將各節點參數疊加，得到整個系統的動力學模型。

1.1 齒輪嚙合模型

1.1.1 時變剛度激勵

齒輪嚙合傳動過程中，齒根處嚙合時彈性變形較小，齒頂處時彈性變形較大，因此嚙合剛度隨時間發生周期性變化。計算嚙合剛度研究比較成熟的方法有石川公式、保角映射法、傅里葉級數展開法等。本文采用修正的梅澤清彥公式計算嚙合線上每點的時變剛度［18］，齒輪副的嚙合綜合剛度計算如下:

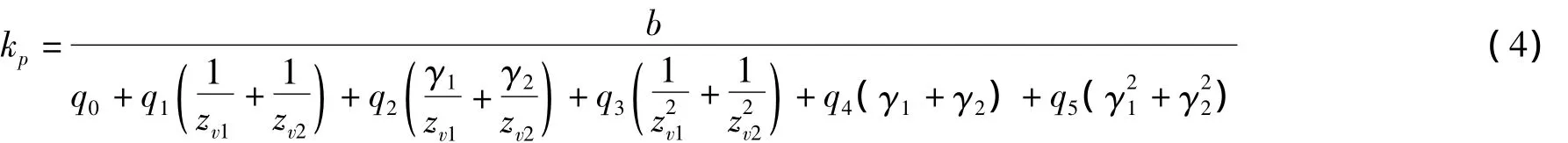
式中:km(t)為齒輪副嚙合綜合剛度;kp為節點處單對齒的嚙合剛度;t為嚙合時間;tz為端平面內轉過一個基節的嚙合時間;ε、εα分別為總重合度系數和端平面內重合度系數;b為有效齒寬;H為齒輪全齒高;q1～q5是由最小二乘法得到的常數，q1=-0.008 54，q2=-0.116 54，q3=2.978 4，q4=-0.006 35，q5=0.005 29;zv1、zv2為當量齒數;γ1、γ2為齒高修正系數。計算得到齒輪嚙合時變剛度如圖1所示，綜合嚙合剛度是一條連續的周期性曲線，這將造成齒輪在嚙合過程中周期性振動。

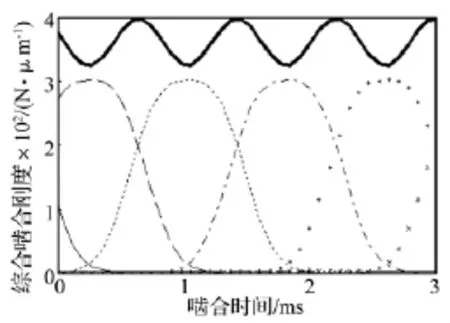
圖1 齒輪嚙合剛度Fig.1 Meshing stiffness for gear pairs

1.1.2 齒側間隙激勵

齒輪系統的受力分析如圖2所示，沿y、z軸方向的齒輪動態嚙合力分別通過Fy、Fz表示。

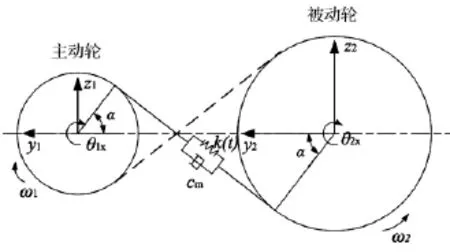
圖2 齒輪嚙合模型Fig.2 Model of gear mesh

輪齒的嚙合傳動會使其產生彎曲和扭轉振動，考慮齒輪彎扭耦合的3自由度模型，齒輪中心處位移可表示為:

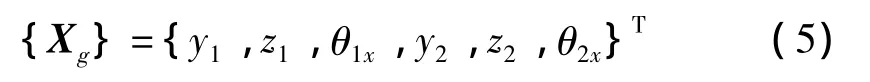
兩齒輪在嚙合線上的相對位移:

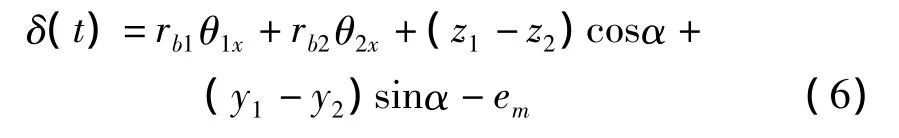
式中:em表示由于實際齒廓偏離理論位置引起的齒輪靜態傳動誤差，α為齒輪壓力角。

當δ(t)＞bn時，齒輪處于正常嚙合狀態;當-bn＜δ(t)＜bn時，齒輪嚙合會出現瞬時脫齒現象;當δ(t)＜-bn時，出現齒背接觸現象。

設齒側間隙為2bn，采用分段函數表示齒側間隙。輪齒間嚙合力包括彈性力和阻尼力，可將時變嚙合力表示為［19］:

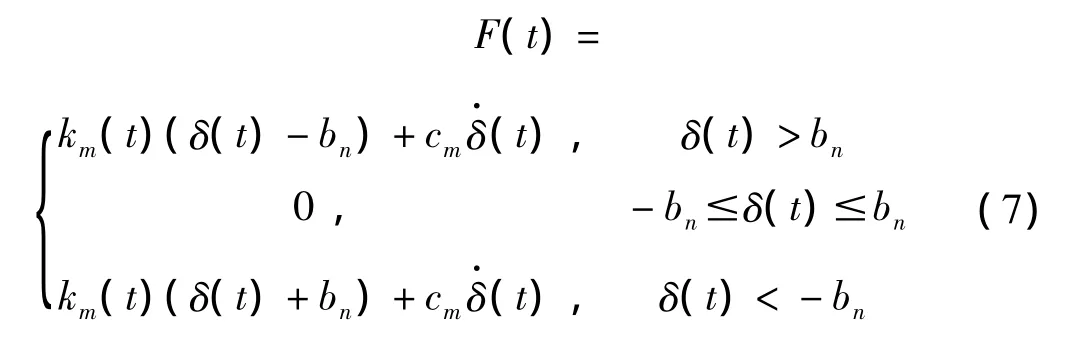
式中:cm是嚙合阻尼。

此外，當沿y方向振動過大時，可能導致齒面、齒背同時接觸，即產生所謂的擠齒現象，發生擠齒條件為:

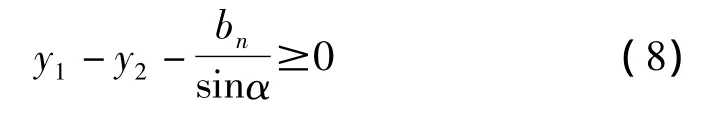
1.1.3 齒輪受力模型

對主動、從動輪進行受力分析，得到受力公式如下:

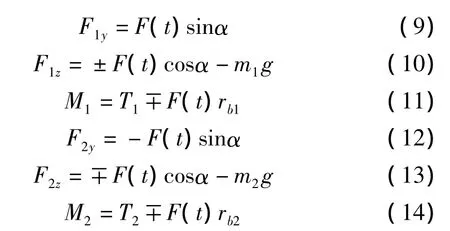
式中:F1y、F1z為主動輪在y，z方向受到的嚙合力;F2y、F2z為從動輪在y，z方向受到的嚙合力;M1、M2表示主、從動輪受到的力矩。rb1、rb2表示主、從動齒輪基圓半徑;m1、m2表示兩齒輪的質量;T1、T2是主、從動輪所受的轉矩。

在正常嚙合狀態下，各公式取上面的符號;當發生齒背接觸時，嚙合力方向改變，各公式取下面的符號。

1.2 滾動軸承非線性接觸力

圖3(a)所示為球軸承，Dw為球徑，D1為軸承外徑，D2為內徑，ur為軸承徑向間隙。圖3(b)為球軸承受力變形后球與套圈之間的位移-變形關系。假設外圈滾道溝曲率中心是固定的，內圈滾道溝曲率中心相對此中心而移動，滾動體質心也產生位移，內外圈接觸角將不同。圖中O1點為固定的外圈曲率中心，內圈溝曲率中心從O2點移動到了O'2點，球中心從Ob點移動到了O'b點。

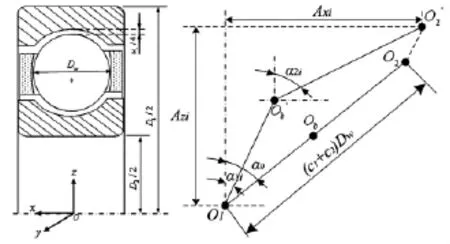
圖3 滾動軸承幾何關系Fig.3 Geometry relation of rolling bearing

圖3中，c1、c2分別為外圈、內圈的溝曲率系數，α0為滾動體與套圈原始接觸角，α1i、α2i分別為受載后第i個滾動體與外圈、內圈的接觸角，Axi、Azi為內外圈溝曲率中心的軸向距離和徑向距離，φi為第i個滾動體的方位角。由圖中幾何關系可求出滾動體與外圈、內圈的接觸變形δ1i、δ2i，以及接觸角，再由赫茲接觸理論可得滾動體和套圈的接觸力Q1i、Q2i。

考慮滾動軸承的離心力、陀螺力矩、慣性力、摩擦力，建立任意受載的滾動體擬動力學分析模型［20-21］。

內圈位移已知時，使用Newton-Raphson方法可求出各滾動體的接觸力。可得滾動軸承的非線性接觸力和力矩為:

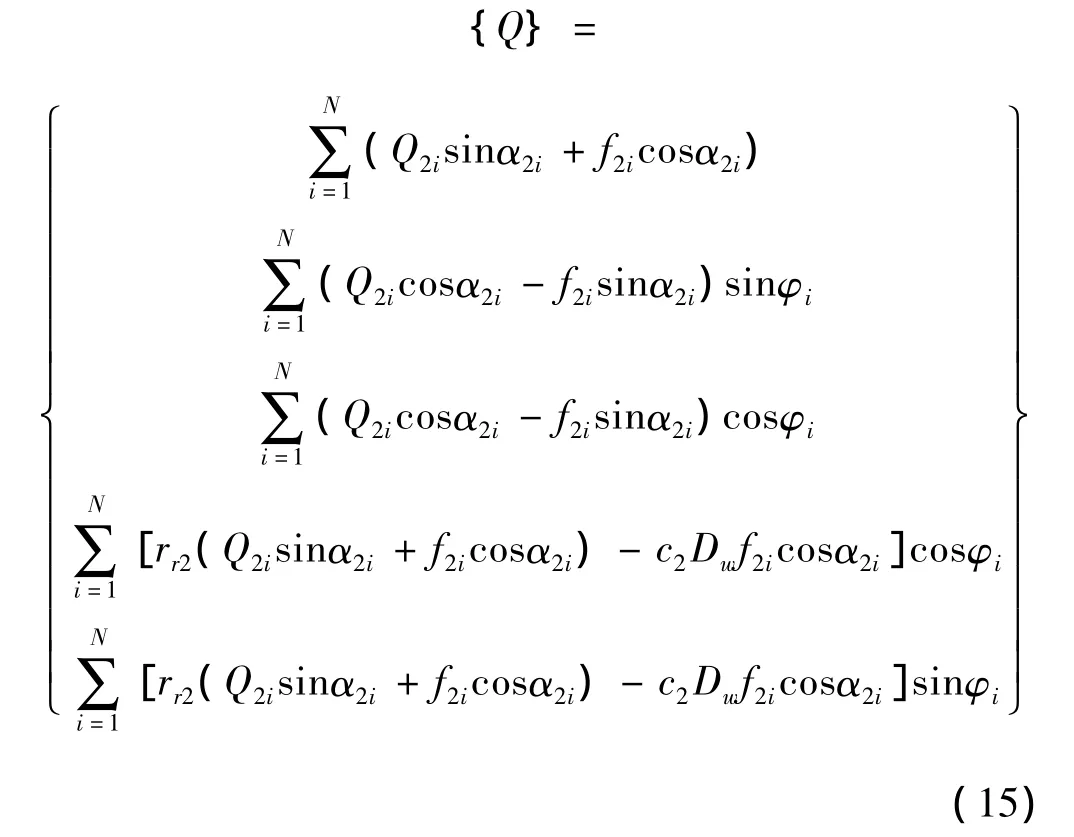
式中:f1i、f2i為滾動體的摩擦力。rr2為內圈滾道溝曲率中心圓半徑。

1.3 彈性轉軸模型

使用有限元理論將彈性軸劃分為若干個軸段，每個軸段單元采用兩節點Euler梁單元模型，每個節點考慮6個自由度，包括橫向彎曲振動(沿y、z軸)、軸向振動(沿x軸)、扭轉振動(繞x軸)、扭擺振動(繞y、z軸)。如圖4所示，兩根彈性軸分別包括n1和n2個節點，i、j表示嚙合齒輪在軸段上的節點位置。

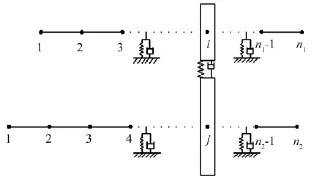
圖4 齒輪軸承轉子系統節點示意圖Fig.4 Nodes of gear bearing rotor system

通過Euler梁單元模型，根據有限元理論，可得到軸段節點的質量、剛度、阻尼、陀螺和載荷矩陣。

1.4 整體法建模

采用整體法對齒輪、滾動軸承和彈性軸的質量、剛度、阻尼、陀螺和載荷矩陣進行組裝。方法如下:

整體法是取各轉子節點狀態向量的集合X=［X1，X2，X3，…，Xn］作為系統的狀態向量，Xi={xi，yi，zi，θxi，θyi，θzi}，每個節點考慮 6 個自由度。組裝維數為6(n1+n2)×6(n1+n2)的質量、剛度、阻尼、陀螺和載荷矩陣。其中，由于齒輪嚙合力考慮3個自由度、軸承力考慮5個自由度，通過對應自由度補零的方法使其添加為6自由度矩陣。

整體法建模組裝各矩陣的流程如圖5所示。首先，輸入初始條件，以齒輪副在轉軸上的節點號ni和nj為基準，將兩根軸的節點號排列為2行的矩陣;然后從轉軸最左端節點開始組裝，將節點的參數矩陣添加到相應的整體矩陣中，若一根轉軸在另一轉軸的對應節點處不存在節點，則將其在整體矩陣中對應的節點設為零矩陣;如該節點處有軸承支承，將滾動軸承質量、阻尼、軸承力矩陣組裝到對應的節點上;對于齒輪耦合節點，考慮到齒輪間的耦合作用，在對應的節點位置上添加齒輪的質量矩陣、嚙合力矩陣;直至所有節點全部組裝，得到齒輪軸承轉子系統的質量矩陣、阻尼矩陣、陀螺矩陣、剛度矩陣、載荷矩陣。

得到各矩陣后，可建立齒輪軸承轉子系統的動力學模型如下:

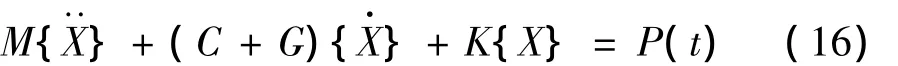
式中:質量矩陣M由轉軸、軸承、齒輪質量組裝得到;阻尼矩陣C由轉軸、軸承阻尼組裝得到;陀螺矩陣G、剛度矩陣K僅包含轉軸項;載荷矩陣P(t)由外力、齒輪嚙合力、非線性軸承力和重力組裝得到。

2 計算方法

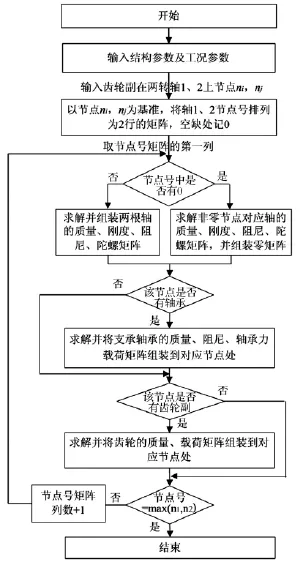
圖5 整體法組裝矩陣Fig.5 Matrix assemble using integration method

根據FPA修正法確定求解周期，采用Runge-Kutta法、Newton-Raphson法對非線性動力學方程組求解，通過時域圖、頻譜圖、相圖以及龐加萊截面圖進行分析。然后求解最大Lyapunov指數，判斷系統的動力學行為。

2.1 求解周期的確定

齒輪軸承轉子系統中，存在齒輪嚙合激勵、軸承非線性變剛度激勵，其中齒輪嚙合力產生的激勵其周期為軸轉動周期的整數倍，但軸承的變剛度激勵周期往往不是軸轉動周期的整數倍，所以在判斷和求解周期運動時，采用修正的FPA法建立統一的求解周期［22］，定義求解周期如下:

式中:T為求解周期，Tg為齒輪嚙合激勵周期，TVC為軸承變剛度激勵周期，ε為常數，取ε=0.01，k=1，2，3，…。

根據上式循環計算，直至找到滿足式(18)的k值，代入式(17)即得求解周期。

2.2 Lyapunov 指數計算

利用Lyapunov指數來判定是否存在混沌響應是目前最有效的方法之一。Lyapunov指數表示在相平面中2條相鄰軌線間的距離隨時間的平均指數發散率，它明確地區分了確定性運動和混沌運動。采用Wolf算法計算最大Lyapunov指數［23-24］，對于連續系統:

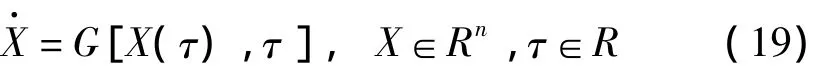
設(τ)為一基準軌線，X(τ)為其相鄰軌線。定義向量X=(x1，x2，…，xn)T的范數為:

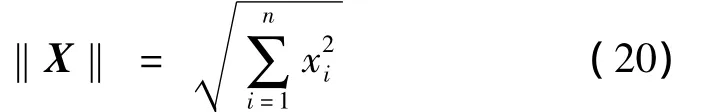
考察X(τ)與(τ)之間的距離隨時間延續的發散程度。記:

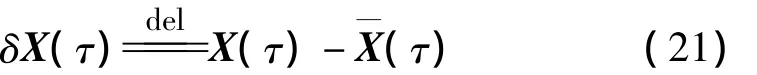
設在τ0時刻‖δX(τ0)‖充分小，于是1維的Lyapunov指數定義為:

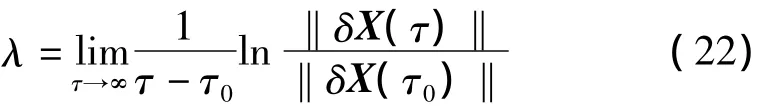
在n維連續系統中，δX(τ)在每個基底上有分量，每一個分量均可求出一個λ，因此共存在n個Lyapunov指數λi，稱為 Lyapunov指數譜。當任意選取向量δX(τ)時，Lyapunov指數以概率1可能取得最大值，如果其中最大的Lyapunov指數λmax＞0，則一定存在混沌運動。因此，只要計算出系統的最大Lyapunov指數，就可以判斷系統是否處于混沌狀態。

3 結果分析

對某齒輪軸承轉子系統進行數值計算，兩齒輪軸長度各400 mm，彈性模量為2×1011Pa，泊松比0.3，各由兩個7306球軸承支承，軸承受預緊載荷200 N，齒輪傳遞扭矩100 N·m。主動、被動齒輪和支承軸承的結構參數如表1、表2所示。

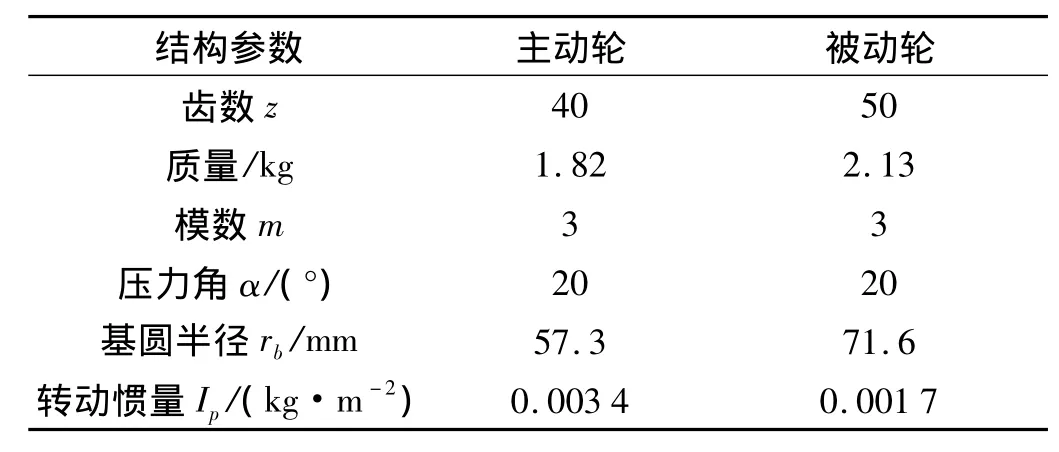
表1 齒輪結構參數Tab.1 Structure parameters of gears

表2 滾動軸承結構參數Tab.2 Structure parameters of rolling bearings

將兩根齒輪軸各劃分為5個節點，分析轉速、齒側間隙、轉軸剛度、軸承徑向間隙對系統非線性響應的影響，本文取從動輪節點處的彎曲振動響應分析。

3.1 齒側間隙的影響

齒側間隙會導致整個系統在運行過程中出現擠齒、脫齒、齒背接觸等現象，造成齒輪單邊沖擊或雙邊沖擊。其他參數不變的情況下，分析齒側間隙對整個齒輪轉子軸承系統的動力學特性的影響。

不同齒側間隙時最大Lyapunov指數隨轉速變化如圖6所示。可以看出，齒側間隙為10 μm時，在2 900～3150r/min，最大Lyapunov指數大于零，系統出現混沌行為;當齒側間隙為20 μm時，系統在2 750～3 300 r/min、4 300～5 400 r/min，系統出現了混沌行為，而當齒側間隙為40 μm時，系統在2 700～ 3 350 r/min、4 150～5 500 r/min，出現混沌行為。隨著齒側間隙的不斷增大，混沌區間逐漸變大。

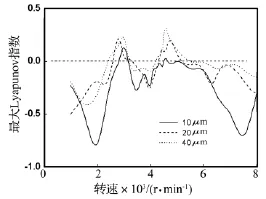
圖6 不同齒側間隙時最大Lyapunov指數隨轉速變化Fig.6 Variation of Maximal Lyapunov exponent with speed at different backlash

計算齒側間隙為20 μm時z方向的振幅，如圖7所示。在2 700 r/min處，振幅出現了跳躍現象。在轉子轉速為4 750 r/min時，出現了共振峰值。這是由于轉速接近齒輪轉子系統一階彎扭耦合振動臨界轉速引起共振。

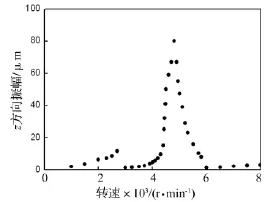
圖7 齒側間隙20 μm時的振幅Fig.7 Amplitude corresponding to 20 μm backlash

齒側間隙為10 μm、轉速為4 400 r/min，沿嚙合線方向相對位移、沿y方向的相對位移、頻譜圖和Poincaré映射圖如圖8所示。可以看出，圖8(a)所示沿著嚙合線的相對位移大于齒側間隙一半，說明齒輪正常嚙合。圖8(b)表示的嚙合產生的y方向的相對位移小于零，根據式(8)中擠齒條件判斷，系統未產生擠齒現象。圖8(c)中頻譜中僅有軸承變剛度振動頻率fb、齒輪嚙合頻率fg，結合圖8(d)Poincaré映射圖為表明系統為周期運動。

齒側間隙為20 μm、4 400 r/min時，相對位移、頻譜圖和Poincaré映射圖如圖9所示。圖9(a)表明沿著嚙合線的相對位移既存在大于齒側間隙一半又存在小于齒側間隙一半的現象，說明系統處于正常嚙合與瞬時脫齒之間，即系統呈現單邊沖擊狀態。圖b)表明嚙合產生y方向的相對位移偶爾會出現大于零的現象，表明系統出現輕微的擠齒。圖9(c)頻譜出現連續譜線，結合圖9(d)Poincaré映射可知系統呈現混沌運動。

圖8 轉速4 400 r/min、間隙10 μm的響應Fig.8 Responses at 4 400 r/min and backlash of 10 μm

圖9 轉速4 400 r/min、間隙20 μm的響應Fig.9 Responses at 4 400 r/min and backlash of 20 μm

齒側間隙分別為 10 μm、20 μm，系統一階彎扭耦合臨界轉速附近4 750 r/min的Poincaré映射圖如圖10所示。圖10(a)表明齒側間隙為10 μm時系統為擬周期振動，圖10(b)表明齒側間隙為20 μm時系統為混沌運動。說明當齒側間隙增大時，系統在一階彎扭耦合臨界轉速附近由擬周期運動進入混沌運動。

以上分析可知，齒輪軸承轉子系統中齒側間隙對非線性動力學行為有重要的影響，隨著齒側間隙增大，齒輪系統會出現脫齒和擠齒現象，進入混沌運動且出現沖擊。

3.2 轉軸剛度的影響

齒側間隙取20 μm，對轉軸剛度的影響進行分析。在其他參數不變的情況下，分別取轉軸長度為300 mm、400 mm、500 mm，轉軸徑向剛度分別為 2.61 ×107N/m、1.14×107N/m、0.59 ×107N/m，分析對齒輪轉子軸承系統的動力學特性的影響。不同轉軸剛度時對應的最大Lyapunov指數隨轉速的變化如圖11所示。

轉軸長度為300 mm時，在2 600～3 700 r/min、4 150～5 900 r/min，出現混沌行為。轉軸長度為400 mm 時，在2 750～3 300 r/min、4 300 ～5 400 r/min，出現混沌行為。轉軸長度為500 mm時，系統在2 800～3 200 r/min，出現混沌行為。可見，隨著轉軸長度增加即轉軸剛度降低，系統混沌區間減小;共振轉速附近產生混沌運動對應的轉速降低，這是由于轉軸剛度降低導致彎扭耦合振動臨界轉速減小，因此混沌運動的區間也發生改變。

轉速為4 400 r/min、轉軸長度為300 mm的響應如圖12所示。圖12(a)表明脫齒現象嚴重，系統出現單邊沖擊。圖12(b)表明，有間歇性的擠齒現象。圖12(c)證明系統為混沌運動。

轉速4 400 r/min、轉軸長度為500 mm的響應如圖13所示，由圖13(a)可知，無脫齒。圖13(b)表明，無擠齒。13(c)證明系統為2周期運動。

對比圖9、圖12與圖13可知，隨著轉軸剛度降低，系統由混沌運動逐漸轉變為2周期運動;由嚴重脫齒逐漸減輕并變為不脫齒，由間歇性擠齒、輕微擠齒變為無擠齒;沖擊現象也逐漸減輕并消失。

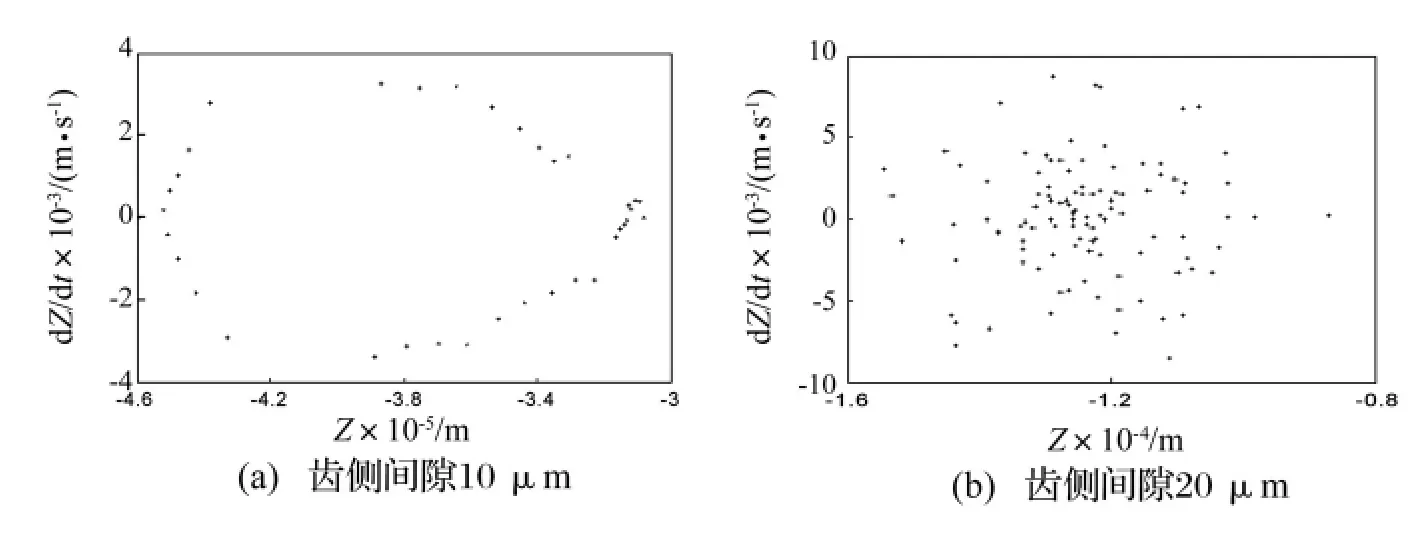
圖10 不同齒側間隙的Poincaré映射Fig.10 Poincaré figuresat different backlash

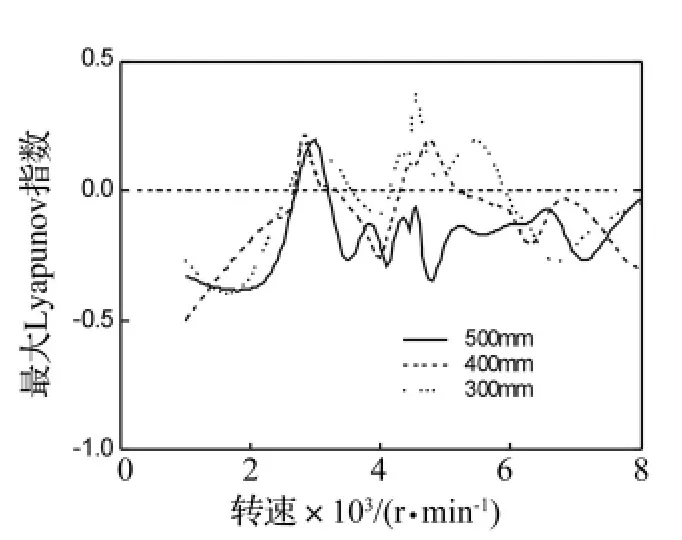
圖11 不同轉軸剛度時最大Lyapunov指數Fig.11 Maximal Lyapunov exponent at different stiffness

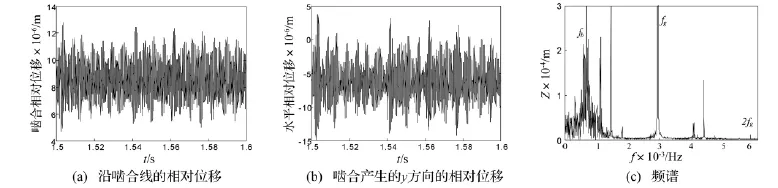
圖12 轉速4 400 r/min、轉軸長度300 mm響應Fig.12 Responses at 4 400 r/min and shaft length is 300 mm

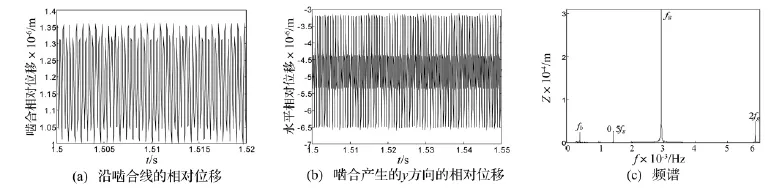
圖13 轉速4 400 r/min、轉軸長度500 mm響應Fig.13 Responses at 4 400 r/min and shaft length is 500 mm

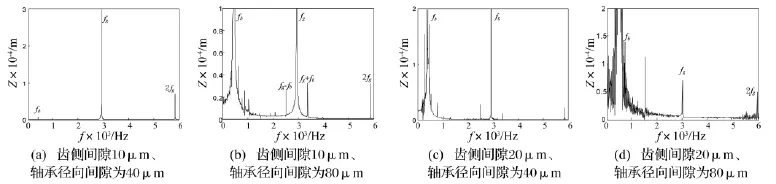
圖14 不同間隙時的頻譜Fig.14 Frequency spectrμm at different backlash and clearance

3.3 軸承徑向間隙的影響

軸承徑向間隙會導致軸承系統出現非線性行為。之前的研究因為軸承的振動幅值與齒輪相比較小而往往忽略，但隨著結構參數與工況參數改變支承軸承的振幅可能很大［13-14］，本文考慮軸承齒輪轉子系統耦合影響，研究軸承的非線性對齒輪的影響。

圖14(a)、(b)給出了轉速4 400 r/min，齒側間隙為10 μm、軸承徑向間隙分別為40 μm、80 μm 時的頻譜圖，與圖8(c)軸承徑向間隙為60 μm時得到的頻譜圖對比，發現徑向間隙為40 μm、60 μm時系統均為周期振動，但間隙為60 μm時軸承激勵的幅值比間隙為40 μm時大;間隙為80 μm時發現嚙合頻率兩側出現軸承振動幅值調制產生的邊頻帶，軸承振動頻率附近出現了連續譜線，軸承變剛度激勵的幅值增大，軸承非線性振動對系統的影響增大，系統由周期運動變為非周期運動。

圖14(c)、(d)給出了轉速4 400 r/min，齒側間隙20 μm、軸承徑向間隙分別為 40 μm、80 μm 時的頻譜圖。與圖9(c)軸承徑向間隙為60 μm得到的頻譜圖對比，發現三種參數下系統均為混沌運動，但隨著徑向間隙的增大，軸承激勵的幅值明顯增大，軸承振動對系統的影響增大，系統的混沌運動行為也變得更加明顯。

4 結論

(1)齒側間隙增大，系統混沌運動的轉速區間變大，振幅出現跳躍現象;齒輪系統會出現脫齒和擠齒現象，由周期運動逐漸進入混沌運動且出現沖擊;臨界轉速附近由擬周期運動進入混沌運動。

(2)隨著轉軸剛度降低，系統混沌運動的轉速區間減少，柔性轉軸對減少系統混沌運動有利;彎扭耦合振動臨界轉速減小;使系統脫齒、擠齒和沖擊現象逐漸減輕。

(3)隨著軸承徑向間隙增大，軸承的非線性振動對系統的影響逐漸增大，軸承變剛度激勵的幅值增大。

［1］王建軍，李其漢，李潤方.齒輪系統非線性振動研究進展［J］.力學進展.2005，35(1):37-51.

WANG Jian-jun， LIQi-han， LIRun-fang. Research advances for nonlinear vibration of gear transmission systems［J］.Advances in Mechanics，2005，35(1):37-51.

［2］Kahraman A，Singh R.Interactions between time-varying mesh stiffness and clearance non-linearities in a geared system［J］.Journal of Sound and Vibration，1991，146(1):135-156.

［3］王立華，李潤方，林騰蛟，等.齒輪系統時變剛度和間隙非線性振動特性研究［J］.中國機械工程，2003，14(13):1143-1146.

WANG Li-hua，LI Run-fang，LIN Teng-jiao，et al.Research on nonlinear vibration characteristics due to time-varying mesh stiffness and gear backlash in gear system［J］.China Mechanical Engineering，2003，14(13):1143-1146.

［4］張鎖懷，沈允文，丘大謀.齒輪耦合的轉子軸承系統的不平衡響應［J］.機械工程學報，2002，38(6):51-55.

ZHANG Suo-huai， SHEN Yun-wen， QIU Da-mou. On response of mass unbalance in a geared rotor bearing system［J］.Chinese Journal of Mechanical Engineering，2002，38(6):51-55.

［5］Kubur M，Kahramang，Zini D M，et a1.Dynamic analysis of a multi-shaft helical gear transmission by finite elements:model and experiment［J］.Journal of Vibration and Acoustics，2004，126:398-406.

［6］ Maliha R，Dogruer C U，Ozguven H N.Nonlinear dynamic modelingofgear-shaft-disk-bearing systems using finite elements and describing functiom［J］.Joumal of Mechanical Design，2004，126:534-541.

［7］ Cai W，Chang J.Strong nonlinearity analysis for gear-bearing system under nonlinear suspension bifurcation and chaos［J］.Nonlinear Analysis:Real World Applications，2010，11:1760-1774.

［8］Cai W，Chang J.Nonlinear analysis for gear pair system supported by long journal bearings under nonlinear suspension［J］.Mechanism and Machine Theory，2010，45:569-583.

［9］ Byrtus M，Zeman V.On modeling and vibration of gear drives influenced by nonlinear couplings［J］.Mechanism and Machine Theory，2011，46:375-397.

［10］崔亞輝，劉占生，葉建槐.間隙非線性齒輪-轉子系統的不平衡響應研究［J］.振動與沖擊，2008，27(S):29-31.

CUI Ya-hui，LIU Zhan-sheng，YE Jian-huai.Research on unbalance response of gear rotor system consider backlash［J］.Journal of Vibration and Shock，2008，27(S):29-31.

［11］崔亞輝，劉占生，葉建槐.齒輪-轉子耦合系統的動態響應及齒側間隙對振幅跳躍特性的影響［J］.機械工程學報，2009，45(7):7-15.

CUI Ya-hui， LIU Zhan-sheng， YE Jian-huai. Dynamic response of geared rotor system and the effect of clearance on jump characteristics of amplitude［J］.Chinese Journal of Mechanical Engineering，2009，45(7):7-15.

［12］陳思雨，唐進元，謝耀東.齒輪傳動系統的非線性沖擊動力學行為分析［J］.振動與沖擊，2009，28(4):70-75.

CHEN Si-yu，TANG Jin-yuan，XIE Yao-dong.Analysis of nonlinear impact dynamic behavior for a gear pair system with time-varying stiffness and friction［J］.Journal of Vibration and Shock，2009，28(4):70-75.

［13］李 明，孫 濤，胡海巖.齒輪傳動轉子-軸承系統動力學的研究進展［J］.振動工程學報，2002，15(3):249-256.

LI Ming，SUN Tao，HU Hai-yan.Review on dynamics of geared rotor-bearingsystems［J］. JournalofVibration Engineering，2002，15(3):249-256.

［14］蔣慶磊，吳大轉，譚善光，等.齒輪傳動多轉子耦合系統振動特性研究［J］.振動工程學報，2010，23(3):254-259.

JIANG Qing-lei，WU Da-zhuan，TAN Shan-guang，et al.Development and application of a model for coupling geared rotors system［J］.Journal of Vibration Engineering，2010，23(3):254-259.

［15］竇 唯，張 楠，劉占生.高速齒輪轉子系統彎扭耦合振動研究［J］.振動工程學報，2011，24(4):385-393.

DOU Wei，ZHANG Nan，LIU Zhan-sheng.The coupled bending and torsional vibrations of the high-speed geared rotor bearing system［J］.Journal of Vibration Engineering，2011，24(4):385-393.

［16］Gupta T C，Gupta K，Sehgal D K.Instability and chaos of a flexible rotor ball bearing system:an investigation on the influence of rotating imbalance and bearing clearance［J］.Journal of Engineering for Gas Turbines and Power，2011，133:1-11.

［17］張偉剛，高尚晗，龍新華，等.機床主軸-滾動軸承系統非線性動力學分析［J］.振動與沖擊，2008，27(9):72-75.ZHANG Wei-gang，GAO Shang-han，LONG Xin-hua，et al.Nonlinear analysis for a machine-tool spindle system supported with ball bearing［J］.Journal of Vibration and Shock，2008，27(9):72-75.

［18］Cai Y.Simulation on the rotational vibration of helical gear in consideration of the tooth separation phenomenon［J］.Journal of Mechanical Design，1995，117:460-468.

［19］李潤方，王建軍.齒輪系統動力學［M］.北京:科學出版社，1997.

［20］Wang L Q，Cui L，Zheng D Z.Study on dynamic property of ball bearing system with nonlinear vibration of rotor［J］.Journal of Mechanical Engineering Science，2008，222(C9):1811-1819.

［21］Harris T A.Rolling bearing analysis(4th Edition)［M］.New York:John Wiley＆Sons，Inc，2001.

［22］ Choi S K，Noah S T.Response and stability analysis of piecewise linear oscillations under multi-forcing frequencies［J］.Nonlinear Dynamics，1992，3:105-121.

［23］ Wolf A，Swift J B，Swinney H L.Determining lyapunov exponents from a time series［J］.Physica D，1985，16:285-317.

［24］ Sundararajan P，Noah S T.An algorithm for response and stability of large order non-linear systems application to rotor systems［J］. JournalofSound and Vibration， 1998，214(4):695-723.