基于電磁超材料的兩種等效參數提取算法的比較分析*

丁敏 薛暉 吳博 孫兵兵 劉政 黃志祥? 吳先良2)?

1)(安徽大學,計算智能與信號處理教育部重點實驗室,合肥 230039)

2)(合肥師范學院物理與電子工程系,合肥 230061)

(2012年6月29日收到;2012年9月17日收到修改稿)

1 引言

電磁超材料(metamaterials)是一種異于天然的人工復合結構或復合材料[1],具有諸如負折 射 效 應[2]、 反 常 Doppler效 應[3]、 反 常Cherenkov效應[4]、完美透鏡[5]等超常物理特性.近年來,對超材料結構實驗方面的研究,已經從最初微波頻段的開口諧振環(SRR)[6,7]和電導線結構逐步深入到光波頻段的漁網結構[8-10].很多學者選用傳統的反演算法[11,12]或基于Kramers-Kronig(K-K)關系[13-15]的改進算法,提取微波頻段超材料結構的等效參數進行研究分析.本文主要利用這兩種算法提取光波頻段超材料結構的等效參數,分析比較兩種算法的準確度與適用性.

為了確定兩種算法的準確度和適用性,我們考慮了兩類具有不同特性的漁網結構.將若干個超材料漁網結構小單元以固定的間隔d沿傳播方向疊加,根據d的取值不同,將結構塊分為弱耦合和強耦合的情況,分別利用兩種算法對不同結構提取等效參數.計算表明,傳統的反演算法適用性很強,對兩類結構的超材料都可以準確地提取等效參數,但計算過程比較復雜;而基于K-K關系的改進算法巧妙地避免了復雜的計算,并能簡單準確地提取材料的等效參數,但其使用范圍具有一定的局限性.

2 算法理論

2.1 傳統反演算法的基本理論

在研究超材料時,一般將其描述為等效媒質.在波長遠大于結構單元的尺寸時,電磁波將不能識別出其內部結構,從而使得超材料可以用有效介電常數和有效磁導率來描述.計算中將超材料結構描述為一種有一定厚度的平板均勻結構,如果得到其傳輸、反射系數的強度大小和相位[8-10],則通過反演計算可以求得復數折射率n和波阻抗z,進一步可以得到媒質的等效介電常數和磁導率[16,17].

本文利用上述原理,對復數折射率n的實部進行研究分析.當平面波垂直入射到一定厚度的超材料結構上時,通過計算或測量得到其傳輸系數T,反射系數R,再利用(1),(2a)和(2b)式,可以得到其波阻抗z和折射率n：

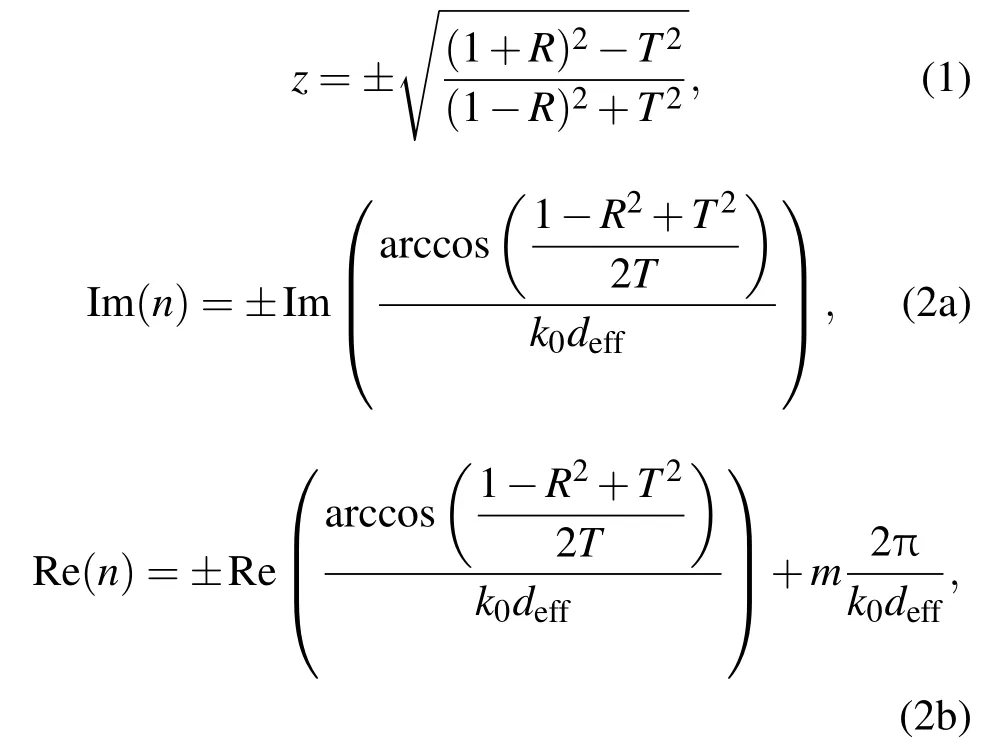
其中,k0是自由空間的波數,deff是超材料結構的有效厚度,m是整數,代表不同分支.

利用超材料自身的特性條件可以確定波阻抗z和折射率n的正負符號.一般非增益超材料要求Re(z)＞0,因此可以得出(1)式的符號.同樣地,Im(n)＞0,就惟一地確定了(2a)及(2b)式的符號,至于分支m的確定需要結合具體的物理概念,比如可依據一般超材料折射率具有連續性等限制條件決定m的具體取值.若是有效厚度deff取值較大,這些分支將十分靠近,很難準確地選擇正確的分支數.傳統反演算法的計算復雜度也就體現在分支數的選擇上.尤其是多層漁網結構[18]的模型,分支選擇的計算量就更大更復雜.

2.2 基于K-K關系的改進算法的基本理論

K-K關系的原理與傳統反演算法基本一致.這種算法的新穎之處在于根據折射率的虛部利用KK關系得到折射率的實部,確保了等效參數的惟一性,避免了分支選擇的復雜性,從而降低了計算的復雜度.K-K關系的本質是利用解析函數的實部和虛部的內在聯系,其物理本質則在于物理系統因果率的體現.

基于K-K關系的算法步驟如下：波阻抗z可由T及R惟一地確定.折射率n的計算涉及一個復對數計算(5)式,這個復對數函數是一個多值函數,但多值性只針對n的實部.這時可用K-K關系由n的虛部來聯系其實部,那么n的實部值就是取最接近K-K關系預測的對數函數對應的分支.但是,此算法要求折射率和頻率是連續的.

該算法需要兩個輸入數據,一是有效厚度deff,即電磁波的傳播方向上所包含的單元格的長度的總和;二是參數T及R.平面波垂直入射到均勻介質板上,波阻抗和折射率與T及R的關系如下：

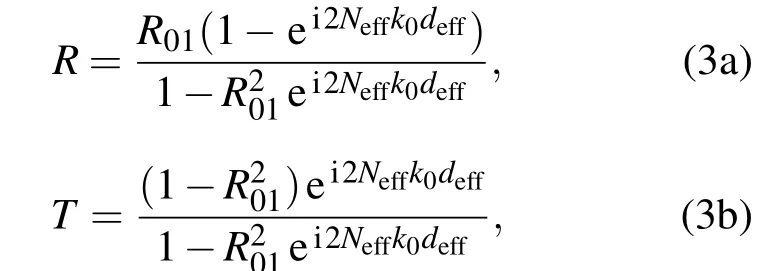
其中,R01=(Zeff-1)/(Zeff+1),Zeff(ω)是復波阻抗,Neff(ω)=neff(ω)+ikeff(ω),是復折射率,neff(ω)是折射率,keff(ω)是消耗系數,k0是自由空間波數,ω是角頻率.

其中,P.V.是柯西主值.

對(9)式可以利用梯形積分規則進行數值計算.但為了避免不當的K-K積分的奇異性,我們可以將積分分成兩個部分,從而可以得到近似的K-K積分：

這里的Round()函數是取最接近的整數.因此,折射率的計算也就是選擇最接近K-K關系預測值的那個分支.

3 數值算例

3.1 開口諧振環組成的超材料模型

首先,選用開口諧振環[6,7]組成的負磁導率超材料模型,分別用傳統的反演算法和基于K-K關系的改進算法提取其等效參數,用來驗證改進算法的適用性.如圖1所示,邊長為2.5 mm的空氣立方體單元模型,中間嵌入厚度為0.25 mm的FR4基板,在基板的一側是厚度為0.017 mm的銅材質開口諧振環.開口環外側邊長2.2 mm,開口間隙0.3 mm,內外環間距0.15 mm,環寬0.2 mm.圖2是開口諧振環模型計算得到的傳輸系數、反射系數和吸收系數的結果.

圖1 開口諧振環模型

如圖3所示,傳統的反演算法和基于K-K關系的改進算法結果基本符合,從而驗證了改進算法的有效性.圖3中曲線neff是用傳統的反演算法計算出的折射率的實部,而曲線nK-K是用基于K-K關系的改進算法計算出的結果,曲線keff是折射率的虛部,根據結算結果可以看出針對此結構傳統方法與基于K-K方法的結果符合得較好,這樣從側面證實了K-K方法的有效性.圖4也給出了基于K-K關系反演得到的磁導率實部隨頻率變化曲線.

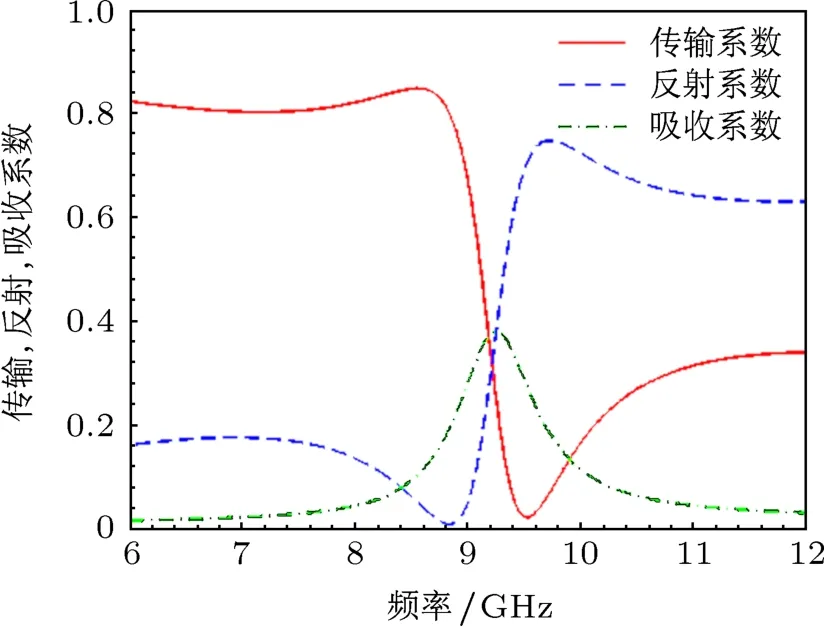
圖2 開口諧振環模型的傳輸、反射和吸收系數

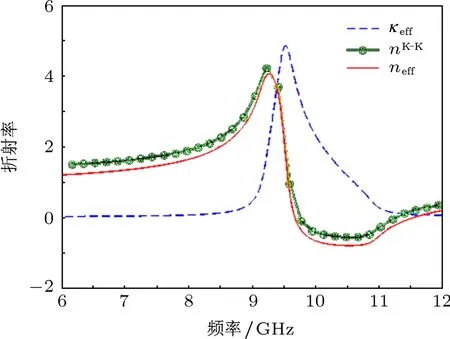
圖3 開口諧振環模型的折射率

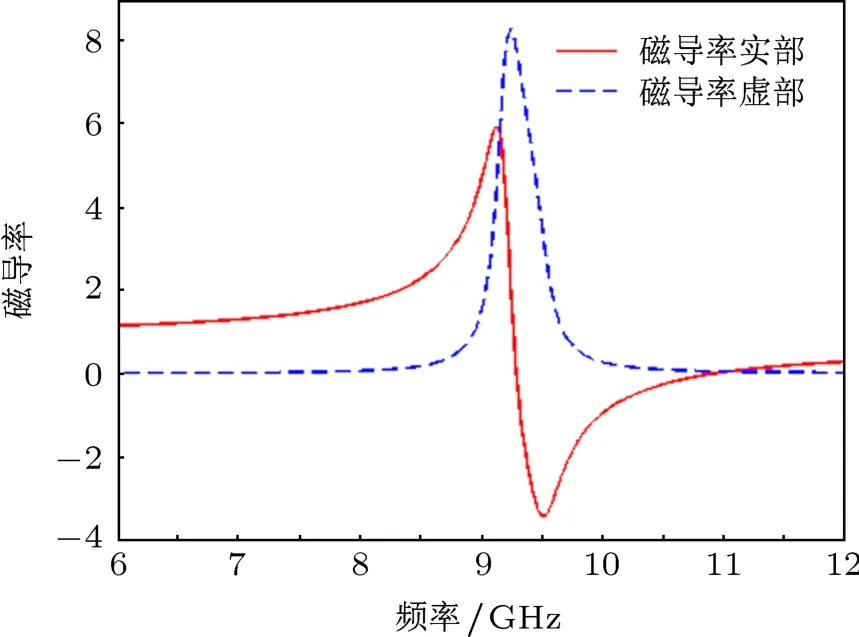
圖4 開口諧振環模型的磁導率

3.2 漁網結構模型

3.2.1 強、弱耦合模型的確定

圖5(a)是超材料漁網結構的一個單元模型[8,18],結構由金屬銀和電介質氟化鎂(MgF2)組成,金屬銀分布在氟化鎂(其介電常數為1.9)兩側.金屬銀是用Drude模型來模擬的,其等離子頻率為1.37×1016rad/s,電碰撞系數為8.19×1013rad/s.傳播方向是沿正z軸方向,結構在傳播方向上是幾何對稱的.其電場方向(E)、磁場方向(H)和波矢方向(k),如圖5(a)所示.其中,ax=ay=860 nm,wx=565 nm,wy=265 nm,s=50 nm,t=30 nm.

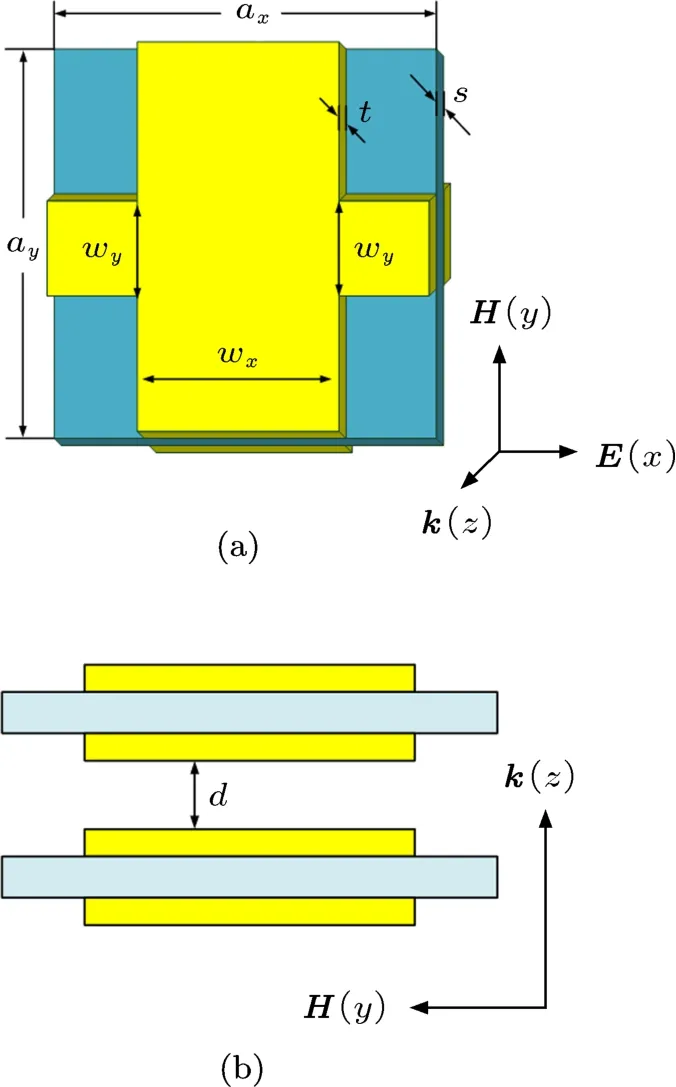
圖5 (a)一個單元模型;(b)7層單元模型疊加的側視圖

圖5(b)是兩個單元模型的疊加,中間由空氣層隔開,間距為d.根據d的取值不同,將疊加的模型分為弱耦合模型和強耦合模型.當d取某個閾值時,每個單元模型之間的相互影響很小,以這個特定的d而疊加的多個單元模型,結構的等效參數將保持穩定,不會隨著結構的疊加而改變,這樣的情況看作是弱耦合模型;當d取值超過閾值時,每個單元模型之間的相互影響很大,近似于光子晶體,這樣的情況看作是強耦合模型.

圖6是該漁網結構的諧振頻率隨d變化的曲線圖.隨著d的增加,結構的諧振頻率也不斷變化.在d取值大于90 nm時,諧振頻率趨于固定值141.6 THz,不再隨著d的增加而變化,即在90 nm處,諧振頻率達到飽和.因此,界定當多個單元模型以d=90 nm為閾值間距沿傳播方向增加時,構成的多層模型稱為弱耦合模型.當d取值小于90 nm的情況均可視為強耦合模型.

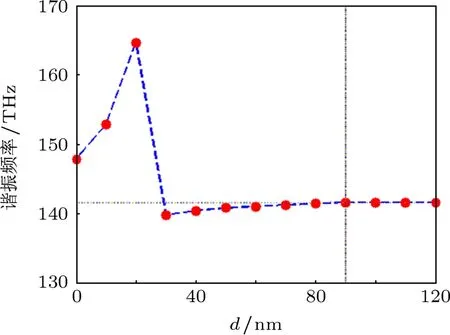
圖6 漁網結構的諧振頻率隨間距d的變化曲線圖

3.2.2 多層弱耦合模型

確定強、弱耦合的閾值后,首先研究的是多層弱耦合模型,由7層單元模型沿傳播方向疊加,每個單元模型之間的間距d=90 nm.圖7是計算得到的傳輸系數、反射系數和吸收系數的結果.

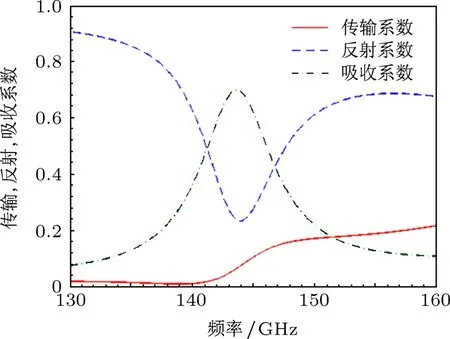
圖7 7層弱耦合模型的傳輸、反射和吸收系數

根據傳輸和反射系數,就可以利用傳統的反演算法和基于K-K關系的改進算法計算出漁網結構的折射率.由于兩種算法計算折射率的虛部的原理基本一致,所以其虛部曲線是完全一致的,也就是圖8中的曲線keff.在圖8中,曲線neff是用傳統的反演算法計算出的折射率的實部,而曲線nK-K是用基于K-K關系的改進算法計算出的結果.可以看出頻率在大概136—150 THz的區域內是負值,這體現了超材料負折射率的奇異特性.由于K-K積分中存在積分近似的過程,折射率的實部曲線nK-K與曲線neff大體趨勢相同,計算結果表明兩種方法在處理弱耦合時的一致有效性.而傳統的反演算法在計算折射率的實部時,需要進行分支選擇,計算過程比較復雜,而基于K-K關系的算法卻巧妙地利用K-K關系得到折射率的實部,具有一定的計算優勢.

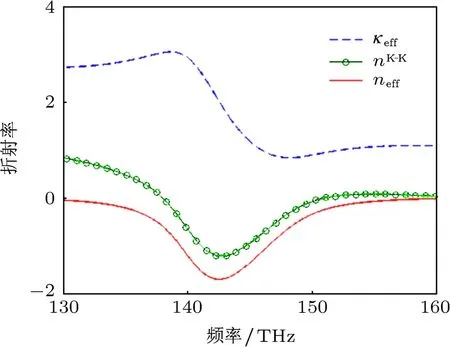
圖8 7層弱耦合模型的折射率

3.2.3 多層強耦合模型

多個單元模型疊加時,其間距d取小于90 nm的情況稱為強耦合模型.此處以d=0 nm為進行數值模擬的強耦合模型.組成強耦合模型的單個模型之間的相互作用較強,所以它的折射率等效參數就會呈現出一些特別的情況,比如不連續的現象.通過計算分析,強耦合模型的折射率確實出現了不連續的情況,所以這時基于K-K關系的算法就無法適用了,因為它要求計算的參數是解析、連續的.

傳統的反演算法可以用于計算不連續的模型,但是比較復雜,因為它涉及具體分支選擇的問題.這里,計算的是19層、23層和27層強耦合模型,通過人工選擇分支確定折射率的值.

圖9是19層、23層和27層強耦合模型的傳輸系數曲線.當頻率f＜136 THz時,傳輸系數T≈0,這是一種金屬特性,也是f＜136 THz時Re(n)≈0的原因.

圖10是折射率實部的不同分支曲線圖,其中：m=1(青色),m=0(藍色),m=-1(紅色),m=-2(綠色),m=-3(品紅色),m=-4(黑色).19層、23層和27層強耦合模型分別是用交叉符號,菱形符號和圓圈表示.

從圖中可以看出,在頻率136 THz附近,折射率的實部出現了不連續現象.頻率小于136 THz時,折射率的實部趨于0.基于傳統的反演算法,根據(2b)式中m的不同選擇及不同層數重疊情形,可以確定出最終折射率實部的曲線如圖10中陰影部分所示.

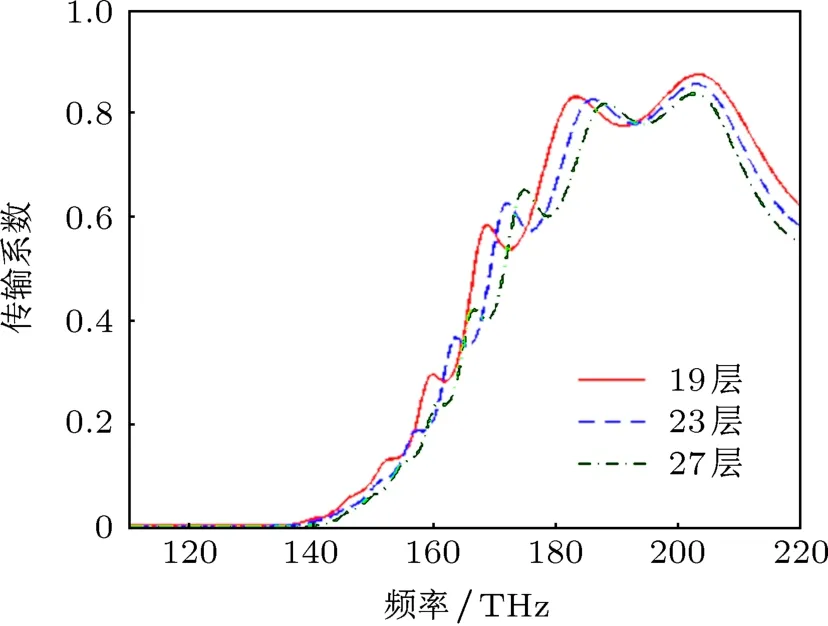
圖9 19層、23層和27層強耦合模型的傳輸系數

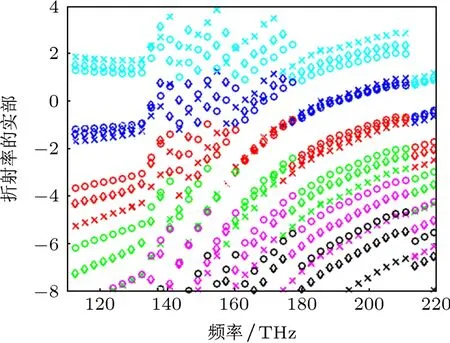
圖10 19層、23層和27層強耦合模型的折射率實部反演結果

4 結論

本文主要利用兩種反演算法分析光波頻段電磁超材料結構的等效媒質理論.給出了多層弱耦合和強耦合結構模型的閾值,利用多層弱耦合和多層強耦合漁網結構模型探討了傳統的反演算法和基于K-K關系的改進算法的適用性及有效范圍.結果表明傳統的反演算法適用性很強,對兩種情況的模型都可以計算其等效參數,但是比較復雜,需人工選擇分支來確定等效參數;而基于K-K關系的改進算法巧妙地利用K-K積分來避免了分支的選擇,但是這種算法又存在一定的局限性,即計算模型的等效參數必須是解析的和連續的.我們的結果為電磁超材料的等效媒質理論提供了新的技術支持.

[1]Veselago V G 1968Sov.Hys.Usp.10 509

[2]Houck A A,Brock J B,Chuang I L 2003Phys.Rev.Lett.90 137401

[3]Seddon N,Bearpark T 2003Science302 1537

[4]Parazzoli C G,Greegor R B,Li K,Koltenbah B E C,Tanielian M 2003Phys.Rev.Lett.90 107401

[5]Pendry J B 2000Phys.Rev.Lett.85 3966

[6]Wang J F,Zhang J Q,Ma H,Yang Y M,Gu C,Qu S B,Xu Z 2009Acta Phys.Sin.58 3224(in Chinese)[王甲富,張介秋,馬華,楊一鳴,顧超,屈紹波,徐卓2009物理學報58 3224]

[7]Li J C,Guo L X,Liu S H 2012Acta Phys.Sin.61 124102(in Chinese)[李俊成,郭立新,劉松華2012物理學報61 124102]

[8]Dolling G,Enkrich C,Wegener M,Soukoulis C M,Linden S 2006Opt.Lett.31 1800

[9]Smith D R 2010Phys.Rev.E 81 036605

[10]Minowa Y,Nagai M,Tao H,Fan K,Strikwerda A C,Zhang X,Averitt R D,Tananka K 2011IEEE Trans.Terahertz Sci.Tech.1 441

[11]Koschny T,Markos P,Economou E N,Smith D R,Vier D C,Soukoulis C M 2005Phys.Rev.B 71 245105

[12]Smith D R,Vier D C,Koschny T,Soukoulis C M 2005Phys.Rev.E 71 036617

[13]Lucarini V,Saarinen J J,Peiponen K E,Vartiainen E M 2005Kramers-Kronig Relations in Optical Materials Research(Berlin：Springer-Verlag)p28

[14]Peiponen K E,Saarinen J J 2009Rep.Prog.Phys.72 056401

[15]Akyurtlu A,Kussow A G 2010Phys.Rev.A 82 055802

[16]Tatartschuk E,Radkovskaya A,Shamonina E,Solymar L 2010Phys.Rev.B 81 115110

[17]Powell D A,Lapine M,Gorkunov M V,Shadrivov I V,Kivshar Y S 2010Phys.Rev.B 82 155128

[18]Valentine J,Zhang S,Zentgraf T,Ulin-Avila E,Genov D A,Bartal G,Zhang X 2008Nature455 376