改進BPR路阻函數及其在EMME中的應用

周彪， 智路平， 李彬

(1. 上海海事大學 經濟管理學院，上海 201306；2. 上海市交通港航發展研究中心，上海 200025)

0 引 言

路阻函數[1]用于描述車輛在道路上的行程費用(或時間)與道路交通條件之間的關系，能反映道路網絡各組成部分的交通容量限制和擁擠效應，是交通量分配預測中的一項十分關鍵的技術，也是實施交通量分配的前提條件.

對路阻函數的研究已有許多成果，有許多不同形式的函數被提出并應用于實踐中.如美國聯邦公路局對大量路段進行交通調查后，通過回歸分析得到BPR函數[2].DAVIDSON應用排隊論基礎提出有漸近性的路阻函數.[3-4]王樹盛等[5]對路阻函數關系式進行推導及擬合分析.王元慶等[6]在“九五”交通科技重點攻關項目關于公路通行能力的研究中，重新標定BPR函數，建立模型.王煒等[7]針對中國國情提出路阻函數修正模型.霍飛[8]結合出行特征進行分析，確定與路阻函數相關的因素并對已有數學模型進行改進.還有基于Greenshields模型的包含速度、交通密度的路阻函數[9]以及在擁擠和非擁擠情況下基于Edie交通流模型的路阻函數[10].其中應用得比較廣泛的是美國聯邦公路局提出的BPR函數

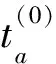
1 改進路阻函數的導出

1.1 改進路阻函數應具備的性質

為保持與BPR函數模型的兼容,改進模型f*(va)應當具有性質(1)～(4)；為彌補BPR函數的內在不足，給改進模型增加性質(5)～(7).

(1)改進路阻函數f*(va)應當是一個嚴格遞增的函數.這符合擁擠效應，也是配流結果具有唯一性的保證.

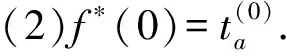
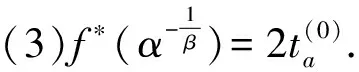
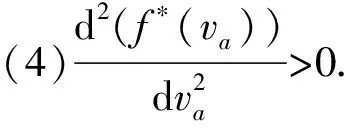
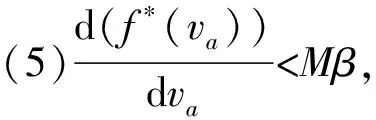
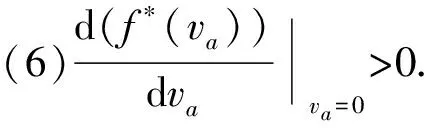
(7)改進路阻模型具……