基于撲克概率的編程算法研究
陳 思
(福州大學 數學與計算機科學學院,福建 福州 350000)
0 背景
德克薩斯撲克全稱Texas Hold’em poker,中文簡稱“德州撲克”。它是一種玩家對玩家的公共牌類游戲。一張臺面至少2人,最多22人,一般是由2-10人參加。德州撲克一共有52張牌,沒有王牌。每個玩家分兩張牌作為“底牌”,五張由荷官陸續朝上發出的公共牌。開始的時候,每個玩家會有兩張面朝下的底牌。經過所有押注圈后,若仍不能分出勝負,游戲會進入“攤牌”階段,也就是讓所剩的玩家亮出各自的底牌以較高下,持大牌者獲勝。因技巧性強,易學難精又被稱為“撲克游戲中的凱迪拉克”。
在這個游戲里,如何根據手頭的牌以及桌面上的牌計算概率,成為勝負的關鍵。與一副牌的已知牌型計算不同,德州撲克不但需要計算牌型的RANK(即排名)值,更需要計算出當前牌型的具體勝率。其中具體的勝率計算非常復雜,筆者將在本文中探討一種可行的方式。
1 游戲介紹
由于本文為概率計算介紹,不在贅述德州撲克中關于籌碼的計算規則,僅把撲克的基本勝負規則做一個闡述。
每個玩家擁有兩張底牌,桌面上將陸續發至5張公共牌。當全部5張公共牌發完后,玩家用自己的2張底牌和5張公共牌結合在一起,選出5張牌,不論手中的牌使用幾張(甚至可以不用手中的底牌),湊成最大的成牌,跟其他玩家比大小。
比牌先比牌型,大的牌型大于小的牌型,牌型一般分為10種,從大到小為:皇家同花順(royal flush):由AKQJ10五張組成,并且這5張牌花色相同;同花順(straight flush):由五張連張同花色的牌組成;4條(four of a kind):4張同點值的牌加上一張其他任何牌;滿堂紅(full house)(又稱“葫蘆”):3 張同點值加上另外一對;同花(flush):5 張牌花色相同,但是不成順子;順子(straight):五張牌連張,至少一張花色不同;3條(three of a kind):三張牌點值相同,其他兩張各異;兩對(two pairs):兩對加上一個雜牌;一對(one pair):一對加上 3張雜牌;高牌(high card):不符合上面任何一種牌型的牌型,由單牌且不連續不同花的組成。
2 問題詳述與分解
在本文中,筆者們的主要問題就是,需要計算玩家的勝率。換句話來說,假設當玩家持有AK(不同花色)時,桌面上為2,3,4,K,Q,且此時共同游戲的玩家有9名 (即競爭對手有8名),這種情況的勝算是多大,就是筆者們需要計算的值。
由于筆者們對于另外8個競爭對手手上的牌一無所知,計算勝率時,筆者們需要窮舉所有的8名玩家可能出現的所有牌型,并一一分析,最后得出實際勝率。
為了研究簡便,筆者們將游戲被分解為這樣的問題:
1)一副牌中,任意取出五張,需要程序馬上計算出它在所有牌型中的排名;
2)已知七張牌中,計算這7張牌能湊出的最大牌型;
3)根據當前公共牌面、人數,窮舉所有情況,并一一對比從而計算勝率(后續內容將證明這種方式并不科學并會給出解決方案)。
本論文中將解決以上問題,并編寫為IPHONE APP。解決問題時,考慮到IPHONE處理器的處理水平,解決過程進行過專門的優化處理。
2.1 牌型的排名
計算牌型的排名涉及到牌型之間的對比。由于上述的分解步驟中,第三部(即窮舉步)將進行大數量級的牌型對比,在這種對比中,每次都調用牌型分析函數是不明智的,筆者們需要將牌型以及其對應的排名一次性計算出來,并予以儲存,方便快速調用。
一副撲克一共有52張,從其中抽出5張的可能性一共有:2598960種可能性。如果將以上情況一一存儲(需要存儲牌值以及排名),至少需要20M左右的存儲空間。這不但會讓整個應用程序變的臃腫,更會大幅降低檢索速度。
本文采取的方式如下:
2.1.1 考慮到德州撲克的牌型大小對比時,不考慮花色。即紅桃10JQKA與黑桃的10JQKA被認為是一樣大。每次計算某5張牌的值時,用這種方式表示當前牌型:
1)不管牌型花色;
2)計算牌型中重復的牌,并對其計數。
編碼規則:
筆者設立了一個長度為52的數組,其中0,4,8,12….48所有被4整除的整數將分別用于代表撲克上的數字,規則是n代表(n/4)+1。在這里筆者們將撲克A計數為1,K計數為13,Q計數為12,而J技術為11。而無法被4整除的數,將用來代表上述數字的牌面,出現了多少次。
舉例來說:紅桃A,黑桃A,方塊K,梅花K,黑桃6這個牌型,經過以上整理,被編碼為:2,50,20。 (例 3.1)
用數學表達來說,假設編碼后的數字為i,j,k,則代表原牌型為:
(i%4+1)張的(i-i%4)/4+1,(j%4+1)張的(j-j%4)/4+1,(k%4+1)張的(kk%4)/4+1
從以上例子來看,2,50,20并不僅僅代表紅桃A,黑桃A,方塊K,梅花K,黑桃6這種情況,實際上,它代表了所有一對A,一對K以及一張單張6的牌型而不管花色如何。
2.1.2 為了方便數據存儲并保證牌型的唯一性(即確保不一樣的牌型筆者們會以不同的數據存儲起來),筆者采用64位隨機數來代表所有牌型。
代碼如下:

PNC數組即代表不同數字(1-K)以及不同數量(1張到4張)的所有情況。以之前的“紅桃A,黑桃A,方塊K,梅花K,黑桃6”牌型為例,如果需要將該牌型進行唯一標識,采取以下方式:
Zobrist=PNC[2]^PNC[20]^PNC[50];//Zobrist即計算出的牌型值,它是唯一的。
2.1.3 有了以上的數組后,即可以通過遍歷所有牌型情況,給每一種牌型進行評分。為了方便計算,采取的方法是將牌型由大到小進行排列,將最大的牌型記為1分,第二大的牌型記為2分,相同的牌型分值相同,以此類推。
相關代碼示例如下:





2.2 概率的計算
根據2.1節所述,我們可以知道當所有桌面牌都被發下后,可以通過簡單的排列組合得出手上兩張牌與桌面5張牌結合中最大的牌型,舉例來說:
玩家手牌:紅桃K,黑桃A
桌面牌:梅花 K,方塊K,紅桃Q,黑桃 J,方塊 10
則最大牌型為順子,即:黑桃A,方塊K(或者其他兩色K),紅桃Q,黑桃J,方塊10。接下來,需要根據手頭的牌型以及桌面的5張牌,計算勝率。由于德州撲克的復雜性,前面說到,如果要精確計算概率,那么其數量級是非常龐大的,當玩家超過3名以后,當前的計算機也無法完成這樣的計算任務。(具體算法如下)
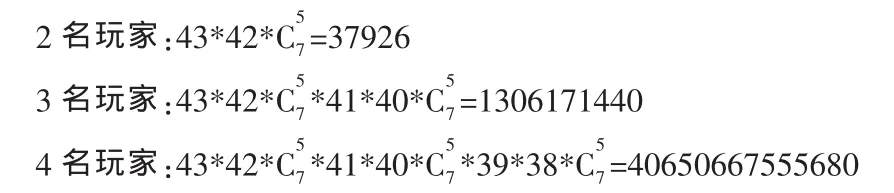
一般德州撲克的玩家是6名以上,這樣計算勝率根本是不現實的。但是,我們注意到,概率計算除了精確計算以外,我們可以采取非精確估計法。
舉例來說,玩家的某個牌型,我們并不清楚其究竟是否會獲勝,我們可以隨機生成其余玩家的牌型,我們把生成完畢的情況稱為一組牌局,每隨機生成一組牌局,我們就對比當前玩家與其他隨機生成玩家的牌型,以計算當前玩家是否獲勝,如果獲勝,就把勝利局數計數器加1,當模擬牌局數量超過某個值時,計算模擬局中當前玩家獲勝的次數與總牌局數量的比值,即為我們想要的勝率。
這樣,我們將一個天文數字的牌局對比,下降到計算機可以接受的程度,以6名玩家為例,總共需要計算的牌型情況為:

如果我們設置總局數為10000局,則計算總數為1260000,該數量級對于計算機來說非常輕松,實際測試中,一臺普通配置的個人電腦可以在3秒內完成該計算。局數越多,則計算出的概率與實際值就越接近,根據2玩家小規模測試,總局數在2000局以上時,計算出的概率已經非常接近于真實值,局數大幅增加雖然讓數字更加接近,但實際意義并不大。
3 總結
通過牌型的存儲與計算以及一種基于概率的非精確算法,我們從一定程度上解決了德州撲克的概率問題,在實際應用中,我們發現這種方法的準確率較高,已經可以從一定意義上指導牌局。當然,隨著技術的發展,應該會有更加先進的算法出現,本文所述的方法也仍有一定的提升空間(如加大模擬局的總數,采取后臺計算等等),后續筆者會持續跟進本項目研究。

