Hsa_circ_0001947對胃癌細胞增殖和凋亡的影響
陳正威,章安偉,張垚,張烜烽,袁海濤,步雪峰
(1.江蘇大學醫(yī)學院,江蘇 鎮(zhèn)江 212013;2.江蘇大學附屬昆山醫(yī)院普外科,江蘇 昆山 215300;3.江蘇大學附屬人民醫(yī)院普外科,江蘇 鎮(zhèn)江 212002)
環(huán)狀RNA是一種特殊非編碼RNA,廣泛存在于生物體內(nèi)[1-2]。其不僅與多種疾病密切相關(guān),且具有潛在的癌癥診斷與生物治療價值[3]。研究顯示,目前已在胃癌患者的胃癌組織、細胞,甚至血漿中發(fā)現(xiàn)多種表達失調(diào)的環(huán)狀RNA[4-6]。Hsa_circ_0001947是一種內(nèi)源性環(huán)狀RNA,定位于X染色體: 147743428-147744289,廣泛表達于人體各組織器官,但其目前在胃癌發(fā)生發(fā)展過程中的作用尚不清楚。本研究擬觀察hsa_circ_0001947在胃癌細胞、組織中的表達,并分析其對胃癌細胞增殖和凋亡的影響。
1 材料與方法
1.1 研究對象
選擇2017年7月至2018年8就診于江蘇大學附屬人民醫(yī)院普外科的75例胃癌患者,行全胃或胃大部切除術(shù)后,收集胃腺癌及癌旁組織(距離癌組織>5.0 cm)標本,手術(shù)標本切除后30 min內(nèi)迅速放入液氮中冷凍,然后于-80 ℃長期保存。標本采集均得到患者同意,并經(jīng)江蘇大學附屬人民醫(yī)院倫理委員會批準。
1.2 細胞株和主要試劑
高通量測序(上海歐易生物醫(yī)學技術(shù)有限公司);人胃癌MGC-803、BGC-823、SGC-7901、HGC-27細胞(中國科學院上海生科院細胞資源中心);正常胃黏膜上皮GES-1細胞株(南京凱基生物科技發(fā)展有限公司);胎牛血清、RPMI 1640、DMEM(以色列BI公司);Trizol試劑(美國Ambion公司);小干擾RNA(si-RNA,廣州銳博生物技術(shù)有限公司);PCR引物(上海生工生物工程股份有限公司);TaqMan反轉(zhuǎn)錄試劑盒(美國Ambion公司);SYBR Green PCR預混試劑、熒光定量PCR試劑盒(日本TaKaRa公司);Lipofectamine 2000轉(zhuǎn)染試劑、CCK-8試劑盒(南京厚載生物科技有限公司);AnnexinⅤ-FITC/PI試劑盒(北京四正柏生物科技有限公司);羊抗兔Cleaved-caspase-3抗體(美國CST公司);羊抗兔Bax抗體、羊抗鼠Bcl-2抗體(武漢博士德生物工程有限公司)。
1.3 方法
1.3.1 細胞培養(yǎng)與細胞轉(zhuǎn)染 用含10%胎牛血清的RPMI 1640、DMEM于37℃,5% CO2飽和濕度的培養(yǎng)箱中分別培養(yǎng)胃癌BGC-823、SGC-7901、HGC-27以及MGC-803細胞。每24 h更換1次培養(yǎng)基,當細胞在培養(yǎng)瓶中覆蓋率達80%時進行傳代培養(yǎng)。細胞接種于6孔板中,當細胞達到50%~70%融合點時,將其分為si-circ_0001947組和si-NC組,分別加入si-circ_0001947,si-NC以及脂質(zhì)體2000,培養(yǎng)12 h,以備后續(xù)實驗用。
1.2.2 實時熒光定量PCR(qRT-PCR)檢測胃組織、細胞中circ_0001947的表達水平 采用Trizol法提取75例胃腺癌、癌旁組織,4種胃癌細胞及胃上皮細胞中總RNA,并按TaqMan RNA反轉(zhuǎn)錄試劑盒說明書操作,將4 ng總RNA反轉(zhuǎn)錄合成cDNA。在CFX96實時定量PCR儀中,以GAPDH為內(nèi)參,量化circ_0001947的表達水平,使用SYBR Green PCR預混試劑行qRT-PCR,以2-ΔΔCt法反映circ_0001947相對表達水平。circ_0001947上游引物:5′-GTGAAACAAACAAAGGTGATGC-3′,下游引物:5′-ATTCCCACTAGGTGATTCTGA-3′,內(nèi)參GAPDH上游引物:5′-CCCACTTCTCTCTAAGGAGAAT-3′,下游引物:5′-TACACGAAAGCAATGCTATCAC-3′。
1.2.3 CCK-8實驗檢測細胞活力 取si-circ_0001947組和si-NC組2組BGC-823、SGC-7901細胞,分別接種于96孔板中,5 000個/孔,每組設置3個復孔,于細胞培養(yǎng)箱中培養(yǎng)。根據(jù)細胞分裂周期分別于0、12、24、48、72 h進行CCK-8檢測[7],每孔加入10 mL CCK-8試劑,置于細胞培養(yǎng)箱中孵育2 h,用酶標儀檢測450 nm處光密度值[D(450 nm)]。
1.2.4 克隆形成實驗檢測細胞增殖 將si-circ_0001947組和si-NC組2組BGC-823、SGC-7901細胞分別接種于6孔板中(500個/孔),每組設置3個復孔,37 ℃培養(yǎng)箱中培養(yǎng)10~12 d;每2~3 d換液一次,克隆細胞長至合適大小時終止培養(yǎng);PBS清洗3次;加入甲醇于4℃固定細胞15 min;PBS清洗3次;每孔加入結(jié)晶紫1 mL染色20 min;加入雙蒸水清洗至洗凈背景;計數(shù)細胞克隆數(shù),克隆形成率(%)=(克隆數(shù)/接種細胞總數(shù))×100%。
1.2.5 流式細胞儀檢測細胞凋亡率 將BGC-823,SGC-7901細胞分別加入si-circ_000194與si-NC培養(yǎng)12 h;收集并消化細胞,用預冷PBS清洗3次;按照細胞凋亡試劑盒說明書操作,先用1×結(jié)合緩沖液重新懸浮細胞,調(diào)節(jié)其密度為1×106/mL;取100 mL懸液,加入5 mL Annexin V-FITC于室溫避光孵育5 min;加入10 mL一碘化丙錠,再加入400 mL PBS,上機進行檢測。
1.2.6 蛋白印跡法檢測凋亡相關(guān)蛋白的表達
將胃癌BGC-823、SGC-7901細胞分別接種于6孔板中,分別加入si-circ_0001947,si-NC孵育12 h后提蛋白。依次行SDS-PAGE,350 mA 90 min濕轉(zhuǎn)至PVDF膜;BSA封閉1h;分別加羊抗兔Cleaved-caspase-3抗體(1 ∶300),羊抗鼠Bcl-2抗體(1 ∶400),羊抗兔Bax抗體(1 ∶400),羊抗鼠β-微管蛋白(1 ∶1 000),4℃孵育過夜;TBST洗膜3次;加羊抗鼠或羊抗兔HRP-IgG(1 ∶3 000)室溫孵育2 h;TBST洗膜3次;增強型化學發(fā)光試劑顯影。Image J對蛋白條帶吸光度進行定量分析。
1.2.7 統(tǒng)計學處理
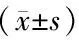
2 結(jié)果
2.1 胃腺癌組織中差異環(huán)狀RNA的表達譜
通過高通量測序篩選出5例臨床胃腺癌、癌旁組織中差異表達的5種環(huán)狀RNA,分別為hsa_circ_0000033,hsa_circ_0000038,hsa_circ_0004916,hsa_circ_0058092,hsa_circ_0001947。與癌旁組織相比,胃腺癌組織中hsa_circ_0000033,hsa_circ_0000038及hsa_circ_0004916表達明顯下調(diào)(t=3.332,2.791,8.901,P均<0.05),hsa_circ_0058092和hsa_circ_0001947表達明顯上調(diào)(t=10.631,15.360,P均<0.01),見圖1。挑選上調(diào)最明顯的hsa_circ_0001947進行后續(xù)實驗。

a : P<0.05,b: P<0.01,與癌旁組織相比
2.2 circ_0001947在胃癌組織及胃癌細胞中的表達
由圖2可見,胃癌組織中circ_0001947相對表達量顯著高于癌旁組織(t=8.019,P<0.01)。4株胃癌細胞中circ_0001947相對表達量均明顯高于人胃上皮GES-1細胞(P<0.05或P<0.01)。circ_0001947在胃癌細胞BGC-823中相對表達量最高,在SGC-7901中最低,故挑選這兩種細胞株繼續(xù)進行后續(xù)實驗。

a : P<0.05,b : P<0.01, 與GSE-1細胞相比
2.3 si-RNA顯著下調(diào)胃癌BGC-823,SGC-7901細胞中circ_0001947表達量
胃癌BGC-823,SGC-7901細胞轉(zhuǎn)染si-RNA 12 h后,si-circ_0001947組中circ_0001947相對表達量明顯低于si-NC組(t分別為10.011,4.933,P均<0.01),由此表明si-RNA對胃癌細胞中circ_0001947存在敲減作用。見圖3。

圖3 si-RNA干預后胃癌細胞內(nèi)circ_0001947表達水平
2.4 下調(diào)circ_0001947表達明顯抑制胃癌細胞增殖
CCK-8結(jié)果顯示,si-circ_0001947組BGC-823,SGC-7901細胞各個時間點D(450 nm)值均明顯低于si-NC組(P均<0.05);circ_0001947組克隆形成率較si-NC組明顯降低(t=9.409,11.381,P均<0.01)。見圖4。

a: P<0.05, b:P<0.01, 與si-NC組比較
2.5 下調(diào)circ_0001947表達促進BGC-823、SGC-7901細胞凋亡
流式細胞儀檢測結(jié)果表明,si-circ_0001947組BGC-823,SGC-7901細胞凋亡明顯高于si-NC組率(t=5.620,3.711,P均<0.01)。見圖5。與si-NC組相比,si-circ_0001947組BGC-823,SGC-7901細胞中Cleaved-caspase-3(t=7.991,12.309,P均<0.01)與Bax(t=8.619,3.574,P<0.01或<0.05)相對表達量明顯升高;Bcl-2相對表達量明顯降低(t=14.527,2.588,P<0.01或<0.05)。見圖6。

圖5 流式細胞術(shù)分析各組細胞凋亡情況

a: P<0.05,b: P<0.01,與si-NC組比較
3 討論
以往研究顯示,環(huán)狀RNA在多種惡性腫瘤中表達上調(diào),通過促進腫瘤細胞增殖,抑制其凋亡影響腫瘤發(fā)生發(fā)展[8-10]。本實驗通過高通量測序挑選出一種新型環(huán)狀RNA hsa_circ_0001947進行研究,實驗結(jié)果顯示,circ_0001947在胃腺癌組織和胃癌細胞中表達水平明顯升高,說明circ_0001947在胃癌發(fā)生發(fā)展過程中可能發(fā)揮原癌基因功能。
張帥等[11]研究表明,環(huán)狀RNA hsa_ circ_0007766通過上調(diào)細胞周期相關(guān)蛋白Cyclin D1/CyclinE1/CDK4表達,從而促進肺腺癌細胞增殖,沉默hsa_circ_0007766表達后,細胞周期阻滯于G0/G1期,明顯抑制肺腺癌細胞生長。楊睿等[12]也證實,hsa_circ_0058514通過影響細胞周期蛋白CCNE1和CKD2表達,從而影響乳腺癌細胞周期。本研究通過CCK-8和克隆形成實驗發(fā)現(xiàn),circ_0001947 促進胃癌細胞增殖,下調(diào)circ_0001947表達后,胃癌細胞增殖明顯受抑制,推測可能與circ_0001947影響胃癌細胞分裂周期有關(guān)。此外,本實驗發(fā)現(xiàn),與正常胃上皮細胞相比,胃癌細胞早期凋亡率與晚期凋亡率均明顯上升。Bcl-2和Bax屬于Bcl家族,是調(diào)控細胞凋亡的重要蛋白,其異常表達會導致細胞凋亡過程失常,增加腫瘤發(fā)生的風險[13-16]。凋亡是影響腫瘤發(fā)生發(fā)展的重要因素[17]。本實驗結(jié)果顯示,敲減circ_0001947后,Cleaved-caspase-3、Bax的表達明顯上調(diào),而Bcl-2表達顯著下調(diào),由此推測circ_0001947在胃癌細胞中可能通過影響凋亡相關(guān)蛋白表達,從而抑制胃癌細胞凋亡。但circ_0001947調(diào)控胃癌細胞周期蛋白與凋亡相關(guān)蛋白表達的具體機制尚有待進一步研究。
綜上所述,hsa_circ_0001947在胃腺癌組織和細胞中呈高表達,其可能通過影響細胞周期促進胃癌細胞增殖,影響凋亡相關(guān)蛋白表達抑制胃癌細胞凋亡。

