不同帶寬高功率電磁環(huán)境對架空線纜耦合效應分析

孟 鑫 周璧華 曲新波

(解放軍理工大學電磁環(huán)境效應與光電工程國家重點實驗室，江蘇 南京 210007)

引 言

國際電工委員會標準IEC 61000-2-13[1]將電場強度超過100 V/m的電磁環(huán)境稱為高功率電磁環(huán)境，主要包括：雷電電磁脈沖(Lightning Electromagnetic Pulse, LEMP)、高空核電磁脈沖(High-Altitude Nuclear Electromagnetic Pulse, HEMP)、高功率微波(High Power Microwave, HPW)和超寬帶(Ultra-Wideband,UWB),眾所周知，高功率電磁環(huán)境對電子、電氣設備及系統(tǒng)的安全運行構成嚴重威脅.隨著信息時代的到來，對高功率電磁環(huán)境的防護問題越來越重要，正受到人們的廣泛重視.值得注意的是，電子、電氣設備及系統(tǒng)中用于傳輸能量與信息的線纜，一旦處于高功率電磁環(huán)境中，通過場線耦合會在設備端口上形成過電流、過電壓，從而造成系統(tǒng)性能降低以致永久性損傷.因而，分析高功率電磁環(huán)境對各類傳輸線的耦合效應對電子、電力系統(tǒng)的防護有重要意義和應用價值[2-4].

國外早在20世紀60年代就已開展場線耦合問題的研究.其中，E. E. Vance[5]最早提出了運用傳輸線(TL)模型來分析架空輸電線路上的感應電流或感應電壓，并給出了架空輸電線終端響應的具體求解公式. M. V. Lanoz[6]給出了計算場激勵下架空線路響應的格林函數(shù)，可方便地用于計算架空輸電線任意點處的感應電流、感應電壓.另外，J. Beilfuss[7]運用模式傳播理論分析了場激勵下多導體傳輸線的響應問題，建立了傳輸線響應的最大值與傳播模式之間的關系，但此方法計算煩瑣，并不被常采用.在E．E Vance研究成果的基礎上，分析電磁脈沖作用下線纜耦合的TL方法在20世紀70年代和80年代得到廣泛應用[8-9]，發(fā)展日益成熟.這種方法的優(yōu)點在于比較簡單，但忽略了天線電流即導體的二次輻射，屬近似方法.隨著計算電磁學的不斷發(fā)展和計算機運算能力的不斷提高，將場線耦合作為電磁散射問題進行時域全波分析已成為可能[10-11].

為分析高功率電磁環(huán)境下架空線纜的耦合效應，本文采用并行時域有限差分(FDTD)算法[12]，分別計算了LEMP(IEC 61643-1)、HEMP(貝爾波形)和HEMP(IEC 1000-2-9)三種電磁脈沖作用下架空線纜的外導體感應電流和終端電壓.為減小計算機內存和計算時間的需求，采用時域卷積PML截斷計算區(qū)域；同時，沿線纜軸線方向采用擴展網(wǎng)格.為進一步提高效率，并行算法得以采用，將原始計算區(qū)域根據(jù)處理器的數(shù)量沿線纜軸向進行一維區(qū)域分解，每個處理器只需計算問題區(qū)域的一部分[13-14]，大大縮短了計算時間.

1 計算模型和方法

1.1 場線耦合模型

電磁脈沖作用下架空線纜耦合模型如圖1所示，平行于地面敷設的架空線長為l，距地面高度為h.架空線兩端接匹配電阻RL，其下端與接地體相連接，接地體為細長導體，埋深1 m.有耗大地相對介電常數(shù)和電導率分別取εrg=10和σg=10-3S/m.電磁脈沖的來波方向由角θ和φ決定.

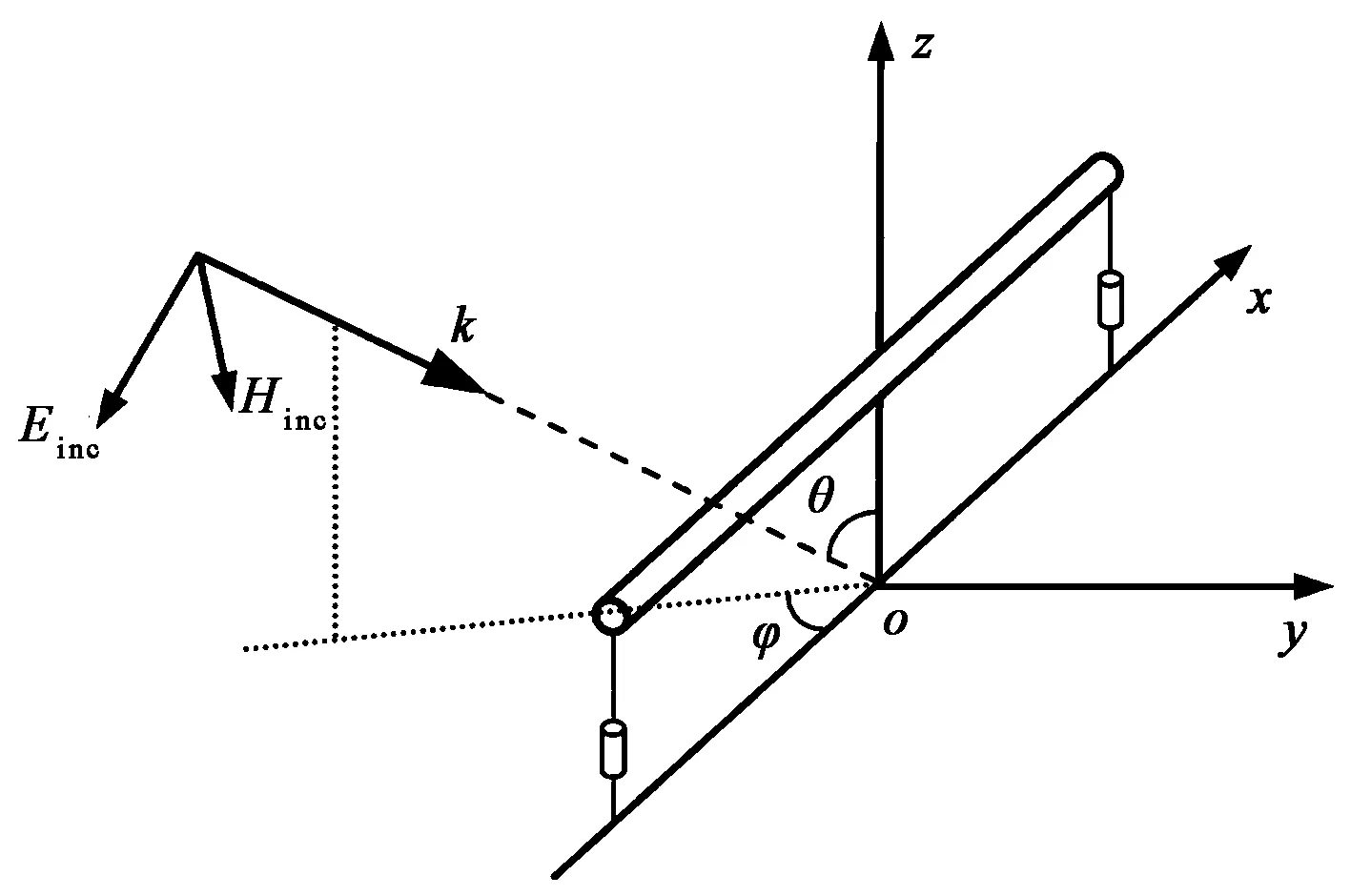
(a) 電磁脈沖激勵架空線纜示意圖

(b) 架空線纜模型剖面圖圖1 場線耦合模型

1.2 激勵源

為比較不同帶寬入射波條件下架空線纜的耦合效應，計算中涉及到三種高功率電磁環(huán)境：LEMP(IEC 61643-1)、HEMP(貝爾波形)和HEMP(IEC 1000-2-9)，本文中分別簡稱為：LEMP，HEMP1和HEMP2，其數(shù)學表達式均采用以下雙指數(shù)函數(shù)表示

E(t)=kE0(e-α t-e-β t)，

(1)

式中：

LEMP：k=1.043,α=1.473×104s-1，β=2.08

×106s-1;

HEMP1:k=1.05,α=4×106s-1，β=4.76×108s-1；

HEMP2：k=1.3，α=4×107s-1，β=6×108s-1.

基于傅里葉變換，雙指數(shù)函數(shù)的頻域解析式為

(2)

其能量的頻譜累積解析式為

(3)

式中w0為總能量.

依據(jù)式(3)，以上三種雙指數(shù)型脈沖的特征參數(shù)列于表1，表中：tr為上升時間；thw為半峰值寬度.相比較而言，LEMP的tr最長，thw最大，頻帶最窄；HEMP2tr最短，thw最小，頻帶最寬.表2給出了三種脈沖不同頻段能量占總能量的百分比.其中，對LEMP而言，99.6%的能量集中在1 MHz以下，最大能量頻段為104～105Hz，該頻段對應波長為幾千到幾十千米級；對于HEMP1，98.2%的能量集中在100 MHz以下，最大能量頻段為106～107Hz，對應波長為幾十到幾百米級；而HEMP2，99.7%的能量集中在1 GHz以下，最大能量頻段為107～108Hz，對應波長為幾米到幾十米級.

表1 三種雙指數(shù)型脈沖波形特征參數(shù)對比

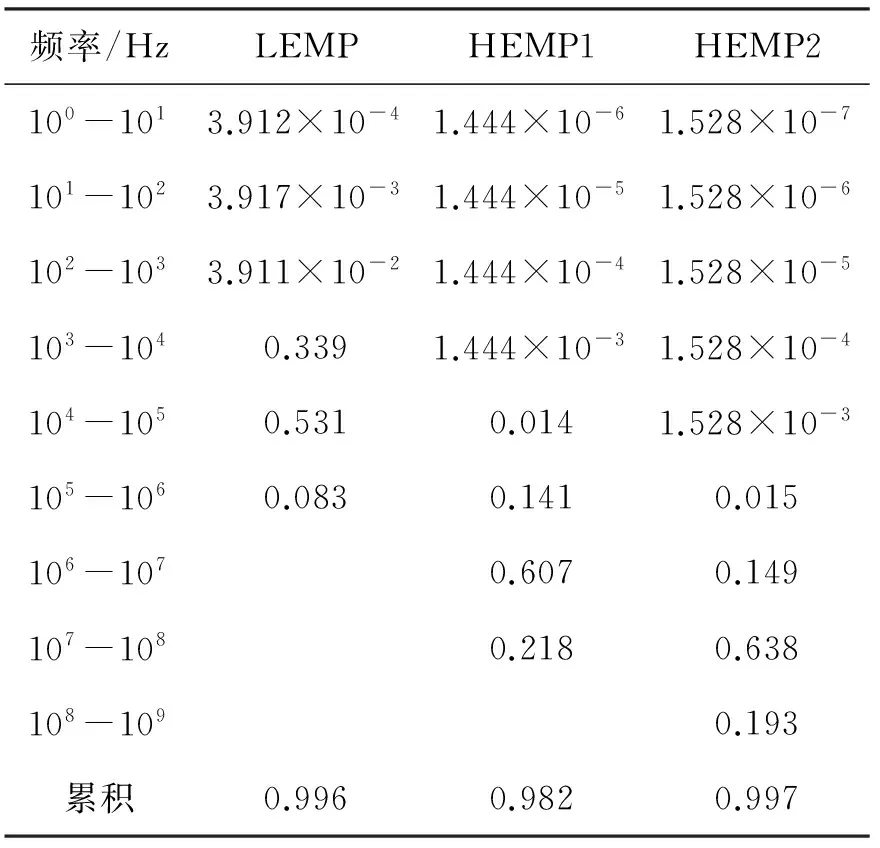
表2 三種脈沖不同頻段能量占總能量的百分比

入射LEMP和HEMP在地面附近視為平面波，其電場時域表達式取以上三種雙指數(shù)脈沖.為了說明入射波的極化方向，在等相位面上規(guī)定一個參考矢量k×z，其中k為單位波矢量，z為z坐標單位矢量.設入射波的電場矢量與參考矢量之間的夾角為ψ，以此來表示入射波的極化方向.

1.3 計算方法

高功率電磁環(huán)境作用下架空線纜耦合屬電磁散射問題，首先利用FDTD法分析圖1所示模型，求出空間電磁場分布，再由安培環(huán)路定律，沿線纜外表面對磁場環(huán)路積分求得外導體電流.整個計算區(qū)域分為地上和地下兩個部分，地上部分為無耗自由空間，采用PML吸收邊界條件截斷計算域，地下部分為有耗空間，需采用有耗介質中的PML吸收邊界條件截斷計算域.用FDTD法計算散射問題時通常將計算區(qū)域劃分為總場區(qū)和散射場區(qū).根據(jù)等效原理，在總場區(qū)和散射場區(qū)的連接邊界上設置入射波電磁場的切向分量可保證入射波只引入總場區(qū).對于空氣-大地分層介質中的散射問題，見圖2，由于受地面的影響，不能簡單地將自由空間中的初始入射波加在連接邊界上.應利用電磁波反射、透射原理，連接邊界地上部分引入的入射波是初始入射波和地面反射波的疊加；地下部分則為初始入射波在地下的透射波[15].

圖2 空氣-大地分層介質總場/散射場

2 計算結果及分析

通過計算三種電磁脈沖與架空線纜耦合的外導體感應電流和終端電壓，研究不同極化方向和不同線纜長度情況下場線耦合效應的變化規(guī)律，并分析引起這些變化的原因.

2.1 不同入射波極化方向對場線耦合效應的影響

為分析不同入射波極化方向對場線耦合效應的影響，取極化角Ψ=0°、45°和90°，h=1 m，θ=30° 和φ=90°，分別計算了三種電磁脈沖入射下架空線纜中點感應電流，計算結果示于圖3～5.

由圖3～5可以看出，不同入射波極化方向對場線耦合效應影響較大，當Ψ=0°即入射電場方向與線纜軸向一致時，耦合效應最嚴重；當Ψ=90°即入射電場方向與線纜軸向垂直時，感應電流很小，耦合效應可忽略不計.

圖3 不同極化方向LEMP入射下架空線中點感應電流

圖4 不同極化方向HEMP1入射下架空線中點感應電流

圖5 不同極化方向HEMP2入射下架空線中點感應電流

2.2 不同線纜長度對場線耦合效應的影響

取h=1 m，Ψ=0°、θ=30° 和φ=90°，分別計算了三種電磁脈沖作用下，架空線纜取不同長度時其中點感應電流和終端感應電壓，計算結果如圖6、7、8所示.

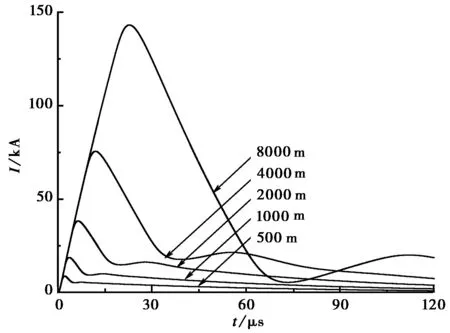
(a) 中點感應電流

(b) 終端感應電壓圖6 LEMP作用下不同長度架空線中點感應電流和終端感應電壓

(a) 中點感應電流

(b) 終端感應電壓圖7 HEMP1作用下不同長度架空線中點感應電流和終端感應電壓

由圖6、7、8可以看出，在三種電磁脈沖作用下，隨線纜長度增加，架空線纜中點感應電流和終端電壓上升沿陡度不變，但峰值變大，波形變寬.當線纜長度與入射波長相比為電小尺寸時，峰值增加較快；當線纜長度增加到一定程度，即線纜長度與入射波能量最集中頻段波長可相比擬時，其峰值變化趨于平穩(wěn)，具體為：當頻帶較窄的LEMP作用時該長度為幾千米以上量級，HEMP1作用時為幾百米量級，頻帶最寬的HEMP2作用時為幾十米量級.另外，在相同條件下，LEMP對線纜耦合效應最強，HEMP1次之，HEMP2最弱，這是由于對相同峰值入射波而言，LEMP總體能量與單位頻段能量最大，而HEMP2總體能量與單位頻段能量最小.

(a) 中點感應電流

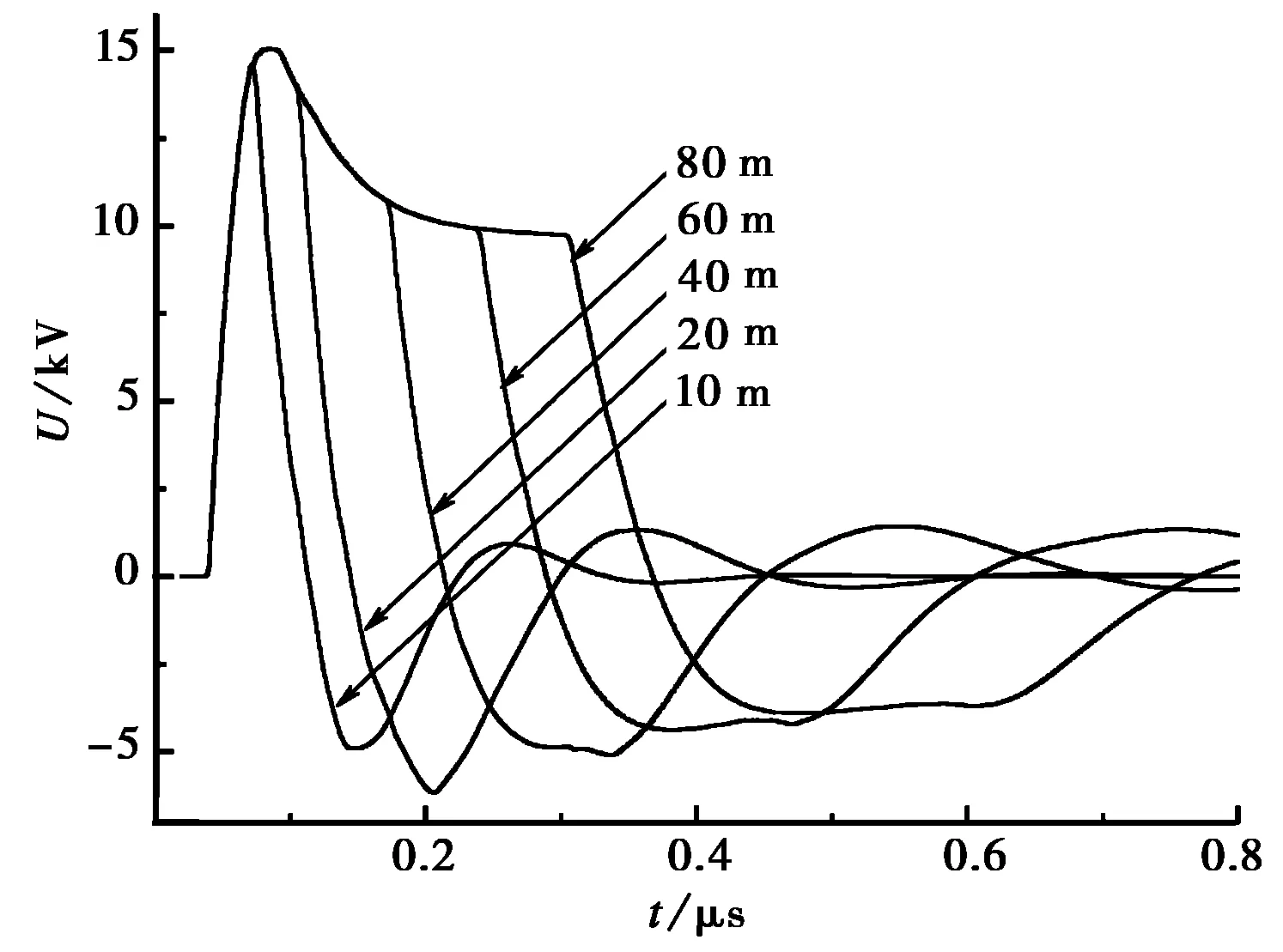
(b) 終端感應電壓圖8 HEMP2作用下不同長度架空線中點感應電流和終端感應電壓

3 結 論

采用并行FDTD技術，研究了在三種覆蓋頻段不同的高功率電磁環(huán)境作用下架空線纜的耦合效應.通過計算架空線纜的外導體感應電流和終端電壓，分析了不同線纜長度、不同入射波極化方向下架空線纜耦合效應的變化規(guī)律.研究結果表明：1)入射波電場方向與線纜走向是否一致或一致的情況如何，將對耦合效應的強弱起決定性影響，當二者一致時，耦合效應最為嚴重；2)線纜外導體感應電流和終端電壓在線纜長度增加時上升沿陡度不變，但峰值有所增加，波形變寬.當線纜長度增加到一定程度，其峰值變化趨于平穩(wěn)，該長度與入射波波長有關：LEMP入射時最長，HEMP2入射時最短；3)在相同條件下，LEMP對線纜耦合效應最強，HEMP1次之，HEMP2最弱.以上結論對于帶有長線纜的電子、電氣系統(tǒng)如何根據(jù)不同高功率電磁環(huán)境的頻譜特征，針對最嚴重的高功率電磁環(huán)境，采取相應的防護措施，具有重要指導意義.

[1] International Electrotechnical Commission. IEC 61000-2-13 Electromagnetic Compatibility(EMC)-Part 2-13 Environment-high-power Electromagnetic(HPEM) Environments-Radiated and Conducted[S/OL]. 1st ed. (2005-03-09)[2012-09-20]. http://www.iec.ch/emc/basic_emc/basic_emc_environment.htm

[2] KODALI V P. Engineering Electromagnetic Compatibility: Principles, Measurements, Technologies, and Computer Models[M]. New York: Wiley Publishing, 1996.

[3] 周璧華, 陳 彬, 石立華. 電磁脈沖及其工程防護[M]. 北京: 國防工業(yè)出版社, 2003.

[4] PAUL C R. Introduction to Electromagnetic Compatibility[M]. New Jersey: John Wiley & Sons, 2006.

[5] VANCE E E. Coupling to Shielded Cables[M]. New York: John Wiley&Sons Press, 1978.

[6] TESCHE F M, LANOZ M V, KARLSSON T. EMC analysis methods and computational models[M]. New York: John Wiley & Sons Press, 1999.

[7] BEILFUSS J, BELL A, GRAY B, ETC. Multiconductor cable response dependency on propagation modes[C]// IEEE International Symposium on EMC, 1988: 2-4.

[8] GREETSAI V N. Response of long lines to nuclear high-altitude electromagnetic pulse[J]. IEEE Trans on EMC, 1998, 40(3): 348-354.

[9] TESCHE F M. Comparison of the transmission line and scattering models for computing the NEMP response of overhead cables[J]. IEEE Trans on EMC, 1992, 34(2): 93-99.

[10] POKHAREL R K, ISHII M, BABA Y. Numerical electromagnetic analysis of lightning-induced voltage over ground of finite conductivity[J]. IEEE Trans EMC, 2003, 45(1): 651-656.

[11] 陳 彬, 王廷永, 高 成, 等. 電磁脈沖作用下近地電纜外皮感應電流的全波分析[J]. 微波學報, 2000, 16(5): 549-593.

CHEN B, WANG T Y, GAO C, et al. Full-wave analysis of the EMP induced current in cables near the ground[J]. Journal of Microwaves, 2000, 16(5): 549-553. (in Chinese)

[12] TAFLOVE A. Computational Electrodynamics: the Finite-difference Time-domain Method[M]. Boston: Artech House, 1995.

[13] 余文華, 蘇 濤, MITTRA R, 等. 并行時域有限差分[M]. 北京: 中國傳媒大學出版社, 2005.

[14] WANG H L, XUE Z H, YANG S M, et al. Near field scattering analysis with parallel FDTD algorithm[C]//IEEE International Symposium on Microwave, Antenna, Propagation, and EMC Technologies for Wireless Communication Proceedings. August 8-12, 2005: 796-799.

[15] YI Y, CHEN B, FANG D G. A new 2-D FDTD method applied to scattering by infinite objects with oblique incidence[J]. IEEE Trans Electromagn Compat, 2005, 47(4): 756-762.