一種改進的符號定時同步算法的研究

趙 亮 李競翔 杜玉海 孫中森

(1．電子信息系統(tǒng)復雜電磁環(huán)境效應國家重點實驗室，河南 洛陽471003；2．中國電波傳播研究所，山東 青島 266107)

引 言

隨著軟件無線電技術的發(fā)展，電磁頻譜管理已不僅僅局限于獲取空間環(huán)境頻譜數據及頻譜參數的測量.若能對接收到的無線信號進行解調，獲取通信內容，頻譜管理的有效性與針對性將會得到極大提高[1].而定時同步是對接收到的信號進行解調的關鍵技術，直接影響到載波同步、信道均衡的性能.在基于軟件無線電技術的數字接收機中，由于采樣時鐘獨立于發(fā)送端符號時鐘，最佳采樣時刻就不能通過直接采樣獲得，只能通過定時誤差估計值控制內插濾波器在最佳采樣時刻內插出近似值.因此，插值濾波是基于軟件無線電的數字接收機一種新的處理方式，完全不同于傳統(tǒng)數字接收機.

本文基于Gardner插值濾波算法, 結合實際情況做出若干改進，克服了其只適用于二相相移鍵控(Binary phase shift keying, BPSK)/正交相移鍵控(Quadrature Phase Shift Keying, QPSK)等兩電平數字基帶調制信號的弱點.實現了四電平全數字16QAM接收機的符號定時同步.

1 符號定時同步基本模型

基于Gardner內插算法的定時恢復結構采用固定頻率的時鐘控制數模轉換器(Analog to Digital Converter, ADC)進行采樣.定時同步模塊由定時誤差檢測器、環(huán)路濾波器和控制器三部分組成.控制器根據環(huán)路濾波器濾出的時鐘相位誤差計算出正確的插值基點mk和插值間隔μk，內插濾波器利用這些信息得到最終的插值信號y(kTi)，實現與發(fā)送端符號速率的匹配.整個算法模型如圖1所示.

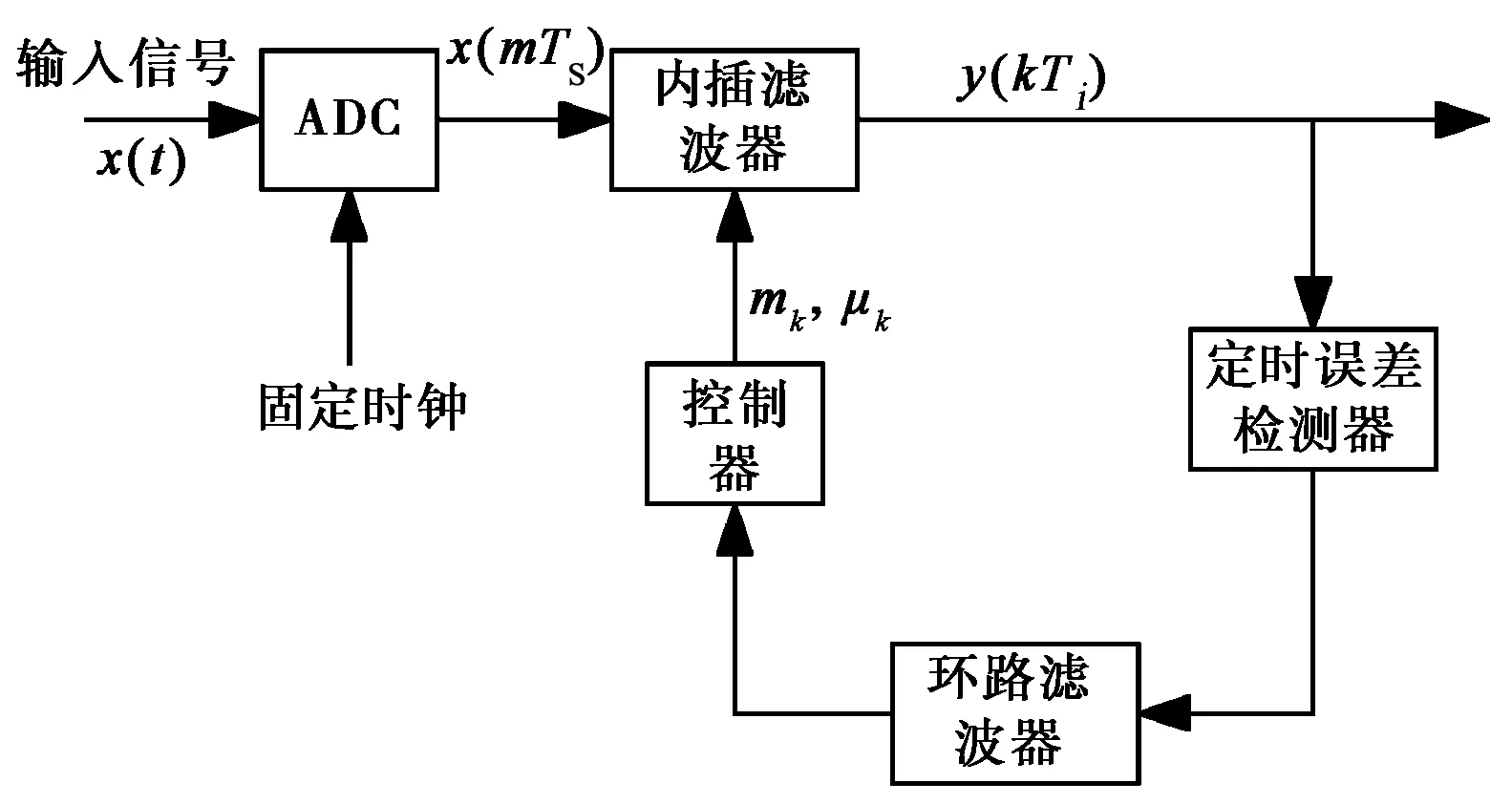
圖1 基于內插濾波器的符號定時同步框圖

1.1 改進的定時誤差檢測器設計

采用Gardner算法[2]的時鐘誤差提取模塊不需要判決反饋，每個符號需兩個采樣點，一個是strobe點，另一個是midstrobe點，兩個最佳觀察點之間的采樣點.該算法每個符號周期計算一次，計算公式為

e(n)=y(n-1/2)[y(n)-y(n-1)].

(1)

同步準確時，如果第n和n-1個樣點的符號相反，則y(n-1/2)樣點應該為零.若第n和n-1個樣點的符號相同，則y(n)-y(n-1)應該為零.如果同步定時準確，則e(n)=0；如果定時超前，無論第n和n-1個樣點的符號相同還是相反，e(n)<0；如果定時滯后，e(n)>0.通過以上算法判定e(n)極性就可以確定同步的調整方向.該算法可以在載波相位鎖定前達到收斂，即與載波相位相互獨立.

Gardner算法是基于二進制調制方式推導出來的.對于四電平16QAM調制信號，存在符號從-1變?yōu)?，1變?yōu)?3、-3變?yōu)?，3變?yōu)?3等情況，當沒有定時誤差時，中間點的平均值并不全部為零.例如符號從3變?yōu)?1，定時準確時，中間點的值為a=(3-1)/2，此時若直接把二進制Gardner算法用在多進制接收機中，定時誤差檢測的結果在某些點上會出現誤判.所以需要對Gardner算法進行改進，使其在沒有定時誤差時，誤差檢測輸出依然為零.經過分析，本文將計算公式修正為

e(n)=[y(n-1/2)-a]·[y(n)-y(n-1)].

(2)

同時，為了進一步降低誤差檢測算法的復雜度,在不影響系統(tǒng)性能的基礎上,本文提出了一種算法改進方案.定時誤差檢測改進算法表達式為

e(n)= {sign[y(n)]-sign[y(n-1)]}·

[y(n-1/2)-a].

(3)

式中：sign(·)是符號函數，

(4)

1.2 改進的內插濾波器設計

內插濾波器實際上實現的是一個數據的速率轉換.

假定接收端固定采樣時鐘為fs，符號周期為T，內插器接收的信號為x(mTs)，Ts=1/fs，通過DAC變換及濾波器hI(t)后，得到一個連續(xù)時間信號的輸出

(5)

根據Gardner在文獻中[2-3]的詳細推導，對于y(t)，在t=kTi時刻對其進行重采樣，可以得到

(6)

式中：mk定義為內插基點，決定輸入序列中哪些采樣點參加內插運算，kTi與mkTs之間的偏差μk為定時誤差，決定了內插濾波器的系數.

一般，有2種方法可用來計算期望的內插值.一種是采用匹配濾波器的多相濾波形式實現內插,這種方法同步精度好,但實現復雜度較高[2-3].所以具體實現時多采用另一種方法——多項式內插，主要包括線性內插、立方拉格朗日內插以及β=0.5的四點分段擬合內插，圖2給出了三種插值濾波器頻域響應的仿真結果.其中以立方插值最接近理想特性，但實現時β=0.5的內插器結構非常簡單，因此，實際中采用此種插值方式.

圖2 三種插值濾波器頻域響應

由于插值濾波器的頻域特性不可能是理想低通的，必將導致插值誤差.而對于16QAM調制信號，由于星座點之間的距離很小，以致能夠容忍的插值偏差非常有限.為了減小插值誤差，可以采用更高階的插值濾波器，但這必然會增加算法的運算量.為了解決這個問題，本文提出了一種改進的插值結構.

在插值濾波器前對信號進行上采樣[4-5]，經過上采樣后，提高了信號的采樣速率，從而壓縮了輸入信號頻譜的混疊范圍，減小在插值過程中由頻譜混疊造成的插值誤差，提高插值濾波器的輸出精度.

改進的插值濾波器結構如圖3所示，對輸入信號進行N(如N=2)倍的上采樣，其中輸入采樣率為fs，輸出的采樣率為Nfs.上采樣后，要保證信號原始特性不變，必須進行低通濾波，以消除上采樣帶來的鏡像頻率.因此，在上采樣后加了一個低通濾波器，這個濾波器可以通過積分級聯梳狀(Cascaded Integrator-Comb,CIC)濾波器實現.

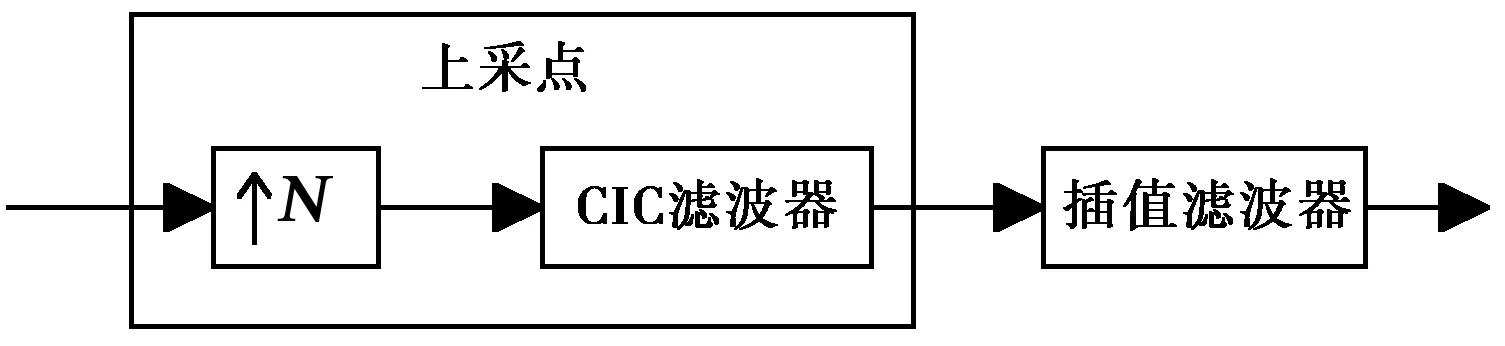
圖3 改進的插值濾波器結構

1.3 環(huán)路濾波器設計

環(huán)路濾波器形式和參數的選取在很大程度上決定了定時恢復環(huán)路的帶寬、收斂時間、跟蹤范圍、抗噪聲性能等,在整個環(huán)路處理中起著重要的作用.這里主要討論二階環(huán)路,文獻[6]給出了環(huán)路濾波器傳輸函數的詳細推導過程.

本文給出離散時域的環(huán)路濾波器的遞歸方程：

y(n)=y(n-1)+c1×[x(n)-x(n-

1)]+c2x(n).

(7)

式中：c1=2×ωn×ζ/K,c2=ω2n/(K×f),ωn,為自然諧振頻率，K為整個定時環(huán)路增益，f為采樣頻率，ζ為阻尼系數，一般取ζ=0.707.

1.4 控制器的設計

環(huán)路控制器的作用就是負責確定插值基點mk和插值間隔μk，并把這些信息提供給插值器使用.控制器主要由數字控制振蕩器(Numerical Comtrolled Oscillator,NCO)和分數間隔計算器組成，NCO的作用是確定內插基點，分數間隔計算器主要計算插值間隔，簡單介紹其工作原理[7].

NCO的差分方程為:

η(m+1)=[η(m)-w(m)]mod1.

(8)

式中，η(m)為NCO寄存器變量.NCO的工作周期是Ts，而內插器的周期為Ti，相位步長w(m)=Ts/Ti+y(n)，y(n)為環(huán)路濾波器的輸出，通過調節(jié)NCO使其在最佳采樣時刻溢出.

μk的計算可使用一個假想的時間連續(xù)的坐標系，坐標系的縱軸為時間連續(xù)的函數η(t)，橫軸為時間t.mk是恰好位于第k個采樣時鐘mkTs.NCO寄存器中的值在t=kTi時刻減小到0.然后跨越了零點，變成小于零，在下一個采樣時刻(mk+1)Ts得到寄存器的值η(mk+1).利用相似三角型原理，很容易得到分數間隔為

(9)

在實際運用中，計算分數間隔時可以用一個近似的固定值來代替ω(m)，從而減小計算復雜度，但同時也會引入一個小的定時抖動.

2 仿真實驗

為了測試本文算法的性能，在加性高斯白噪聲(Additive White Gaussian Noise,AWGN)信道下，針對一個全數字16QAM解調系統(tǒng)，進行了計算機仿真.設帶通噪聲帶寬與調制信號帶寬相等；信噪比為23 dB；調制信號符號速率、符號定時偏差、采樣頻率進行了歸一化，分別選定為1、0.03、4；基帶平方根升余弦濾波器滾降系數取0.35；現給出仿真結果.

圖4所繪的是接收端環(huán)路收斂后插值濾波器輸出的結果.可以看出:未成形基帶信號經滾降系數為0.35的根升余弦濾波器后已變的不再規(guī)則，但插值濾波器輸出的最佳采樣點依然可以準確的重構出原始的基帶數據.其中中間采樣點即為前文所述的兩個最佳觀察點之間的采樣值.

圖4 定時同步后插值濾波器輸出

圖5為定時同步后恢復的基帶數據所繪的星座圖.由圖可見，發(fā)送信號已被精確恢復，可以此數據為基礎進行進一步的0、1判決.

引入0至2π范圍內任意一個隨機的載波相偏，圖6以相偏為π/8為例給出解調星座圖.可以看出，雖然含有載波相偏，但定時同步環(huán)路并未受到影響，星座圖已被正確恢復(含有的載波相偏要靠載波同步環(huán)路糾正).

圖5 定時同步后解調星座圖

圖6 引入載波相偏、定時同步后解調星座圖

在歸一化后符號速率為1的前提下引入0.2的載波頻偏.由于16QAM信號星座圖呈矩形排列，16個向量點中共包含三種大小的幅度矢量，若定時同步完成后，正確的星座圖應呈現三個圓環(huán)旋轉排列(星座圖旋轉的原因是存在載波頻偏，而載波頻偏要靠載波同步環(huán)路糾正)，圖7的仿真結果表明定時同步后得到的星座圖與以上的的分析是吻合的，定時同步環(huán)能夠完全獨立于載波頻偏,先于載波同步環(huán)完成定時偏差調整.

圖7 引入載波頻偏、定時同步后解調星座圖

為進一步驗證定時環(huán)路性能,在AWGN信道下，針對不同符號定時偏差及載波頻偏進行了10 000次定時同步實驗.在信噪比為16 dB、歸一化符號速率為1的前提下，環(huán)路正常工作最大可承受的符號定時偏差為0.03，載波頻偏為0.4.定時環(huán)路可在4000余個符號內能夠完成同步，成功概率可達99.9%，這表明在較低的信噪比及大偏差的條件下，本算法的性能還是相當優(yōu)異的.

3 外場實驗

該算法已在XILINX芯片上成功實現，并已嵌入到某衛(wèi)星頻譜管理設備中.圖8即為接收到的亞洲五號衛(wèi)星在12.34 GHz頻率上的一段信號的頻譜圖.其中最右側選中的信號為16QAM調制.

圖9為對該信號解調后輸出的星座圖，由圖可見，發(fā)送信號已被恢復，但聚斂的程度較差，這是由于現有的衛(wèi)星接收天線增益較小，接收信號信噪比較差(信噪比約為12 dB)的原因造成的.

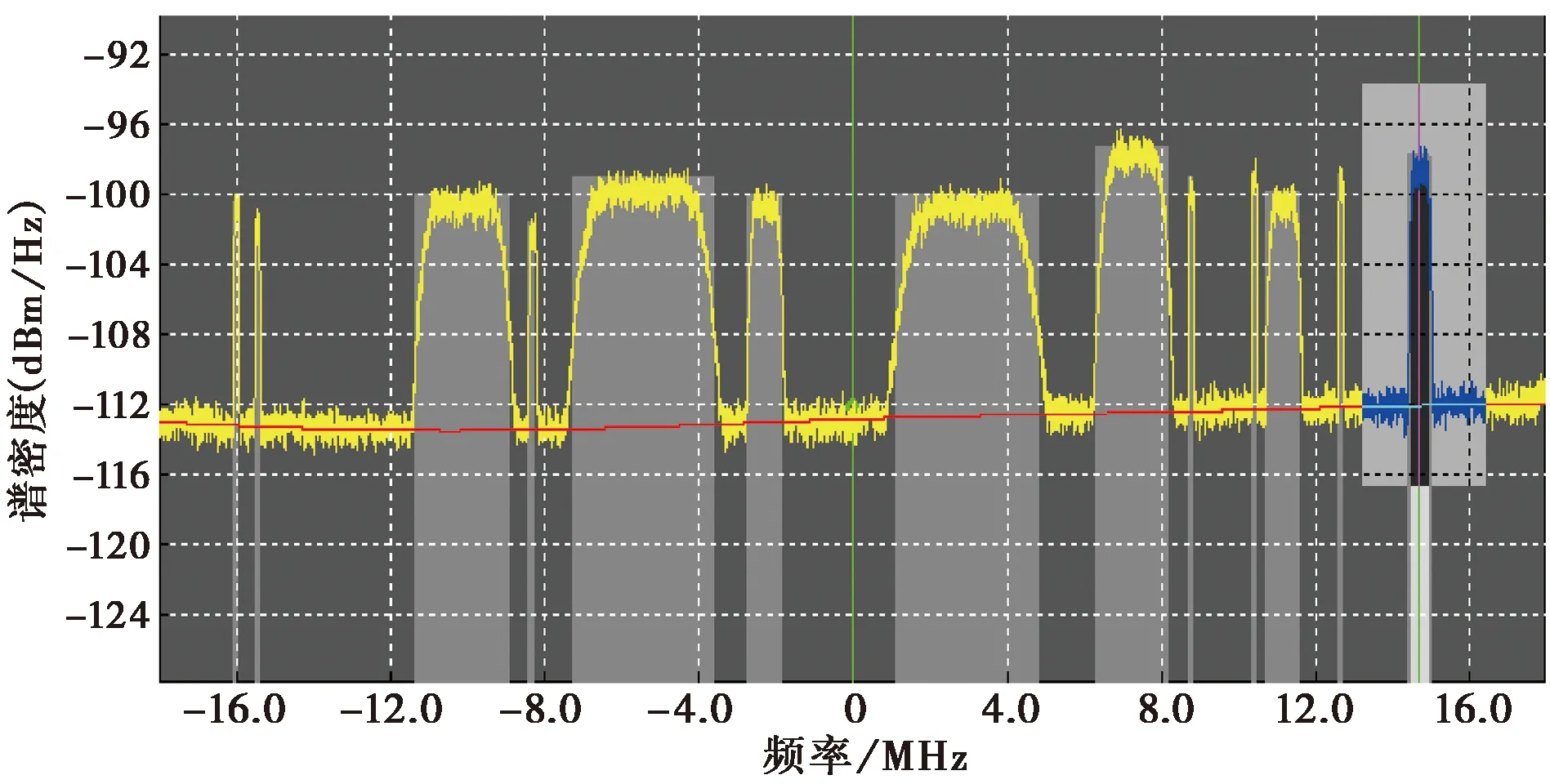
圖8 接收到的衛(wèi)通信號頻譜圖

圖9 16QAM信號解調星座圖

4 結 論

本文采用改進的Gardner 誤差檢測算法和一種新的插值濾波器設計方法對16QAM信號進行符號同步，實現了四電平調制信號符號的定時同步，改進的插值濾波器同時提高了定時恢復的精度，且實現復雜度低，在全數字解調尤其是衛(wèi)星通信、移動通信中有較高應用價值.

[1] 孫正波,葉尚福. 利用互模糊函數實現衛(wèi)星干擾源定位[J]. 電波科學學報, 2004, 19( 5) : 525-529.

SUN Zhengbo, YE Shangfu. Satellite interference location using Cross Ambiguity Function[J] . Chinese Journal of RadioScience, 2004, 19(5):525-529.(in Chinese)

[2] GARDNER F M. A BPSK/QPSK timing-error detector for dampled receivers[J]. IEEE Trans Commun, 1986,34 (5):423-429.

[3] GARDNER. Interpolation in digital modems-Part I :fundamental[J] IEEE Trans Commun,1993, 41(3):501-508.

[4] ERUP L , GARDNER F M, HARRIS R A. Interpolation in digital modems-Part II: implementation and performance[J].IEEE Trans Commun, 1993, 41 (6):998-1008.

[5] LIN D M. A modified Gardner detector for symbol timing recovery of MPSK signals[J].IEEE Trans Commun, 2004, 52(10):1643-1647.

[6] 趙君偉 ,姜泉江 ,劉會杰. 一種基于低軌衛(wèi)星通信的定時同步研究[J]. 無線電通信技術, 2009,35(5):19-22

ZHAO Junwei, JIANG Quanjiang, LIU Huijie . Research on timing synchronization for LEO satellite communication [J].Radio Communications Technology, 2009,35(5):19-22.(in Chinese)

[7] 趙 渝，郭見兵，陳東進. 全數字接收機中定時恢復的研究 [J]. 光通信研究, 2011, 6(3):61-63.

ZHAO Yu,GUO Jianbing, CHEN Jindong. Study of timing recovery in all-digital receives[J]. Study on Optical Communications, 2011, 6(3):61-63.(in Chinese)