基于選擇性注意機(jī)制的無邊界主動(dòng)輪廓圖像分割算法
李 蕙,王延江
(中國石油大學(xué)信息與控制工程學(xué)院,山東青島266580)
圖像分割是把圖像分成互不交疊的有意義的區(qū)域,每個(gè)區(qū)域內(nèi)的像素都具有相似性,而在邊界處則具有非連續(xù)性。常用的圖像分割算法可分為三類:基于邊界的算法、基于區(qū)域的算法和基于特定理論的算法。Kass等人提出的主動(dòng)輪廓模型[1]是較有代表性的基于變分的圖像分割算法,該算法在全局能量函數(shù)框架下求取最優(yōu)解,但存在對(duì)初始值比較敏感,不具有自動(dòng)拓?fù)渥兓芰Φ葐栴}。因此,研究人員相繼提出了許多改進(jìn):Cohen等提出了“氣球”模型[2];Caselles 等[3]和 Malladi等[4]分別提出了幾何活動(dòng)輪廓模型(geometric active contours);后來Caselles等又提出了測(cè)地主動(dòng)輪廓模型(geodesic active contours)[5];Saddiqi等提出在測(cè)地線模型基礎(chǔ)上增加“面積最小項(xiàng)”[6]來進(jìn)一步阻止邊界泄漏;Xu等提出了幾何GVF活動(dòng)輪廓模型[7];而后Chan等在Mumford-Shah模型[8]基礎(chǔ)上又提出了無邊界主動(dòng)輪廓模型(active contour without edges)[9]。上述算法從不同方面對(duì)主動(dòng)輪廓模型進(jìn)行了改進(jìn),但仍然存在一些問題,如需要人為給定初始化輪廓線或掩膜(mask),對(duì)于復(fù)雜圖像和多目標(biāo)圖像分割效果不夠理想等。受人類視覺感知機(jī)制的啟發(fā),筆者將選擇性注意機(jī)制引入到無邊界主動(dòng)輪廓模型,提出一種基于選擇性注意機(jī)制的無邊界主動(dòng)輪廓圖像分割算法。
1 無邊界主動(dòng)輪廓模型概述
主動(dòng)輪廓模型可分為兩類:基于邊界的方法和基于區(qū)域的方法。前者存在結(jié)果易受圖像噪聲影響,對(duì)于初始輪廓線的位置較敏感,難以得到全局性分割等問題;而后者則從圖像模型的角度出發(fā),給出圖像模型應(yīng)滿足的全局能量泛函,通過最小化能量泛函來驅(qū)動(dòng)輪廓線的膨脹與收縮,這類方法不僅抗噪性能更強(qiáng),而且能夠收斂到全局最優(yōu),其中,最具有代表性的是Chan等于2001年提出的無邊界主動(dòng)輪廓模型[9]。
無邊界主動(dòng)輪廓模型(又稱為分段常量模型)是一種全局最優(yōu)的分割方法,認(rèn)為所分的兩個(gè)區(qū)域(目標(biāo)和背景)都是均質(zhì)的,并應(yīng)用二相的水平集方法來進(jìn)行數(shù)值求解。假設(shè)給定一幅圖像I(x,y),則無邊界主動(dòng)輪廓能量泛函表示如下:
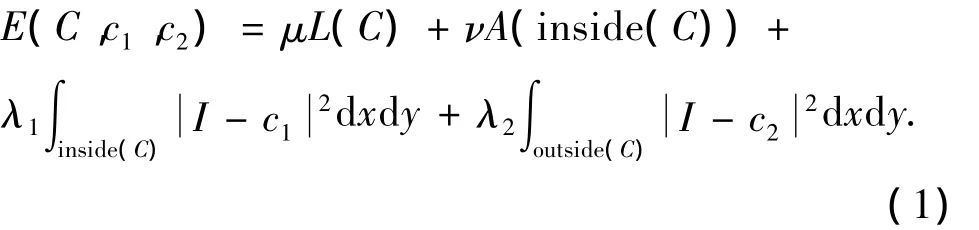
其中,C為封閉邊界;c1和c2分別為輪廓線內(nèi)部區(qū)域和外部區(qū)域的平均灰度;μ ≥0,ν≥0,λ1,λ2> 0為固定參數(shù),μ為約束邊界長度的參數(shù),ν為約束閉合輪廓面積的常數(shù),λ1和λ2分別為控制輪廓線內(nèi)外能量權(quán)重的參數(shù);長度約束L和面積約束A用于控制輪廓線的光滑度和規(guī)則度。當(dāng)輪廓線位于區(qū)域間邊界時(shí),E(C)才能取到最小值。
通過引入Heaviside函數(shù)和Dirac函數(shù)可將能量函數(shù)式(1)規(guī)范化。此外,Chan與Vese由拉格朗日方法推導(dǎo)所得的水平集演化方程如式(2)所示:
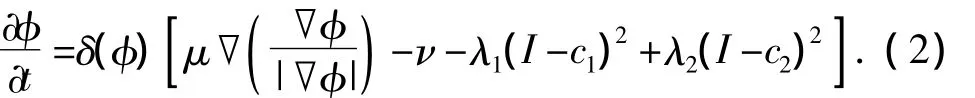
其中,φ為符號(hào)距離函數(shù),且內(nèi)正外負(fù),其更新迭代方程為
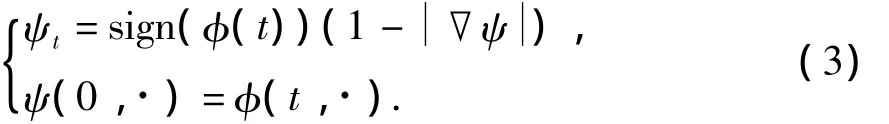
在實(shí)際的數(shù)值計(jì)算中,分別采用正則化函數(shù)式(4)代替Heaviside函數(shù)和Dirac函數(shù):
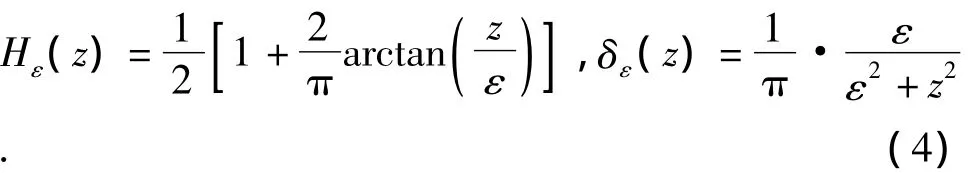
其中,ε為常數(shù)。
上述過程可使水平集演化方程作用于所有的水平集上,進(jìn)而使能量函數(shù)達(dá)到極小值,并且得到圖像分割的結(jié)果。該方法與傳統(tǒng)主動(dòng)輪廓方法相比,抗噪能力有所增強(qiáng),降低了對(duì)于初始化的要求,不需要依靠圖像中的邊緣信息,可有效分割出模糊或者離散的邊緣。此外,由于使用了水平集,從而使得輪廓線的拓?fù)渥兓艿玫阶詣?dòng)的處理。
2 基于選擇性注意機(jī)制的無邊界主動(dòng)輪廓圖像分割模型
通過對(duì)人類視覺感知系統(tǒng)的深入研究,本文中提出一種基于選擇性注意機(jī)制的無邊界主動(dòng)輪廓圖像分割模型,將選擇性注意機(jī)制引入到基于區(qū)域的無邊界主動(dòng)輪廓模型中以取代傳統(tǒng)人工方式完成掩膜初始化,該模型主要包括圖像預(yù)處理、掩膜初始化和迭代分割等部分。算法流程如圖1所示。
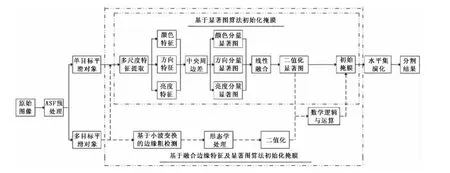
圖1 算法流程圖Fig.1 Flow chart of proposed algorithm
2.1 利用迭代開閉運(yùn)算的預(yù)處理
ASF(alternating sequence filter)算子由 Sternberg[10]提出,而后又經(jīng) Serra[11]進(jìn)行了廣泛的研究和完善。本文通過構(gòu)造ASF算子[12]對(duì)輸入圖像做平滑預(yù)處理,具體定義如下:
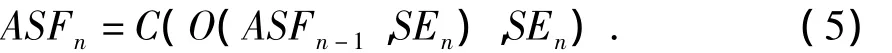
式中,ASFn-1為濾波前的原始圖像;O表示開運(yùn)算,即先腐蝕后膨脹;C表示閉運(yùn)算,即先膨脹后腐蝕;n為開/閉運(yùn)算的次數(shù);SEn是半徑為n的圓盤結(jié)構(gòu)元素。數(shù)學(xué)形態(tài)學(xué)中的開運(yùn)算可以去掉凸角,而閉運(yùn)算則具有填充凹陷的作用,選取合適的結(jié)構(gòu)元素(本文選用3×3的disk結(jié)構(gòu)元素)以及n值,反復(fù)進(jìn)行開閉運(yùn)算即可得到平滑區(qū)域,如圖2所示,其中,(a)列和(b)列的第一行分別為輸入的原始圖像,第二行為預(yù)處理后得到的平滑圖像。與其相對(duì)應(yīng)的直方圖分別為(c)和(d)。通過直方圖的對(duì)比可知,對(duì)圖像的平滑預(yù)處理使區(qū)域之間的能量分布更加明顯,有利于后續(xù)的分割工作,并且能有效減少迭代次數(shù)。
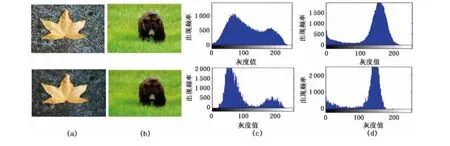
圖2 基于ASF算子的圖像預(yù)處理Fig.2 Image preprocessing based on ASF operator
2.2 基于顯著圖的掩膜初始化
目前的無邊界主動(dòng)輪廓模型大多是由人為來確定初始掩膜,分割結(jié)果和效率受主觀性影響較大。對(duì)于單目標(biāo)圖像,考慮到算法效率,可以通過提取顏色、亮度、方向等初級(jí)特征構(gòu)造顯著圖,進(jìn)而初始化掩膜。本文中采用基于顯著圖的方法初始化掩膜,使得掩膜的位置更加貼近于感興趣目標(biāo),從而能夠有效減少迭代次數(shù)。構(gòu)造顯著圖的過程以亮度特征為例,首先構(gòu)造不同尺度的亮度高斯金字塔的圖像序列,并記中央周邊差算子為Θ,可得

式中,I(c)為細(xì)尺度圖像;I(s)為粗尺度圖像;c取{1,2,3},而 s=c+m,m 為{3,4},因此 s的取值范圍是{4,5,6}。
然后應(yīng)用歸一化算子N(·),將上述的特征差異圖像進(jìn)行融合得到亮度分量顯著圖,該步驟的生物學(xué)依據(jù)在于算子近似模擬了大腦皮層的側(cè)抑制生物機(jī)制(即近鄰相似特征可以通過特定的聯(lián)結(jié)來相互抑制)。其具體實(shí)現(xiàn)如下:
(1)歸一化亮度特征圖的像素值至0~M,用以消除特征圖的多模態(tài)尺度差異;
(2)計(jì)算特征圖的像素均值ˉm;
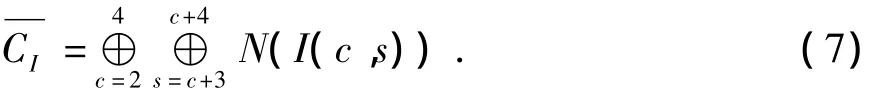
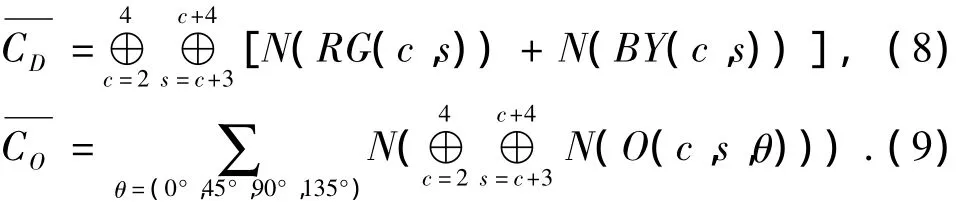
式中,RG(c,s)和 BY(c,s)分別表示紅色 - 綠色的反差對(duì)比以及藍(lán)色-黃色的反差對(duì)比;O(c,s,θ)表示圖像在不同的尺度和不同的方向上的梯度對(duì)比。
最后加權(quán)融合可得到顯著圖S,將其二值化后即可作為本文算法初始化掩膜:

用上述方法對(duì)包含單個(gè)目標(biāo)的靜態(tài)圖片進(jìn)行掩膜初始化,結(jié)果如圖3所示。其中,第一行為原始圖像,第二行為顯著圖,第三行為本文中基于顯著圖確定的初始掩膜。
當(dāng)圖像中存在多個(gè)目標(biāo)時(shí),傳統(tǒng)手動(dòng)選定掩膜的方法不僅效率不高,而且如果掩膜選取不當(dāng)則極易出現(xiàn)漏分割的現(xiàn)象。若僅僅采用以上基于顯著圖的方法確定掩膜,那么多個(gè)目標(biāo)可能會(huì)合成一個(gè)較大的掩膜區(qū)域(圖4(c)),對(duì)迭代的效率有不利影響。因此,對(duì)于多目標(biāo)圖像,采用融合邊緣特征及顯著圖的算法來初始化掩膜。其流程如圖1所示,具體如下:首先,應(yīng)用上述方法得到顯著圖;然后,通過小波變換的方法實(shí)現(xiàn)對(duì)圖像的邊緣粗檢測(cè),由于A Tuous算法不需要抽取偶數(shù)樣本,奇異檢測(cè)更為準(zhǔn)確,因此本文中采用基于小波的二維A Tuous算法[13]以二階樣條小波函數(shù)和合適的尺度J進(jìn)行計(jì)算,得到邊緣粗檢測(cè)圖;最后將邊緣粗檢測(cè)圖與前述顯著圖進(jìn)行數(shù)學(xué)邏輯與運(yùn)算,最終得到初始化掩膜。結(jié)果可見圖4,其中,(a)為原始圖像,(b)和(c)分別是其顯著圖及基于顯著圖確定的掩膜,(d)為邊緣粗檢測(cè)圖與顯著圖的邏輯運(yùn)算結(jié)果,(e)為本文基于融合邊緣特征的顯著圖算法確定的掩膜。
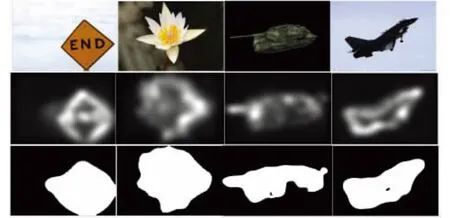
圖3 基于顯著圖的掩膜初始化(單目標(biāo))Fig.3 Saliency map based mask initialization(single target)

圖4 基于顯著圖的掩膜初始化(多目標(biāo))Fig.4 Saliency map based mask initialization(multiple targets)
2.3 算法步驟
本文算法具體步驟如下:
(1)首先,輸入靜態(tài)圖像I。
(2)利用迭代開閉運(yùn)算進(jìn)行平滑預(yù)處理,得到區(qū)域能量聚集而邊界又相對(duì)清晰的平滑圖像If。
(3)初始化掩膜。當(dāng)原始圖像I中存在單個(gè)目標(biāo)時(shí),采用基于顯著圖的算法初始化掩膜;當(dāng)原始圖像I中存在多個(gè)目標(biāo)時(shí),采用融合邊緣特征及顯著圖的算法初始化掩膜。如此自動(dòng)得到的掩膜位置和大小較接近于待分割目標(biāo)的真實(shí)位置和大小,且不像傳統(tǒng)方法那樣受主觀性影響。
(4)求取窄帶(narrow band)[14]。使得計(jì)算主要集中在輪廓線周圍的像素上而非整幅圖像,從而很大程度上降低了計(jì)算量和復(fù)雜度,并能使輪廓線盡快收斂。
(5)求取當(dāng)前能量函數(shù)值E,迭代直到能量函數(shù)值達(dá)到最小或達(dá)到所設(shè)定的迭代次數(shù)M。
(6)輸出圖像分割結(jié)果。
3 實(shí)驗(yàn)結(jié)果和討論
為了驗(yàn)證本文算法的正確性和有效性,分別應(yīng)用無邊界主動(dòng)輪廓模型以及本文提出的算法進(jìn)行圖像分割實(shí)驗(yàn)。實(shí)驗(yàn)在64位windows 7環(huán)境下運(yùn)行,計(jì)算機(jī)配置Intel 2.5GHz處理器,2GB內(nèi)存,MATLAB R2009a軟件平臺(tái),實(shí)驗(yàn)所采用的圖片來源是公開的顯著圖像庫以及internet。
實(shí)驗(yàn)中應(yīng)用無邊界主動(dòng)輪廓模型時(shí)隨機(jī)選取其初始掩膜。當(dāng)圖像中僅存在單個(gè)目標(biāo)時(shí),采用本文中基于顯著圖的方法進(jìn)行掩膜初始化;當(dāng)圖像中存在多個(gè)目標(biāo)時(shí),采用本文中針對(duì)多目標(biāo)的融合邊緣特征的顯著圖方法進(jìn)行實(shí)驗(yàn)。此外,本文采用像素點(diǎn)統(tǒng)計(jì)量與收斂時(shí)間相結(jié)合的方法量化實(shí)驗(yàn)結(jié)果以進(jìn)行比較。基準(zhǔn)圖來源于公開的顯著圖像庫或人工標(biāo)定。像素點(diǎn)統(tǒng)計(jì)量主要包括目標(biāo)像素點(diǎn)數(shù)、漏檢點(diǎn)個(gè)數(shù)、誤檢點(diǎn)個(gè)數(shù)以及相應(yīng)的正檢率和誤檢率。其中,目標(biāo)像素點(diǎn)數(shù)即所得分割區(qū)域中目標(biāo)區(qū)域的像素點(diǎn)總數(shù)目,漏檢點(diǎn)數(shù)即分割結(jié)果中未檢出的目標(biāo)像素點(diǎn)數(shù),誤檢點(diǎn)數(shù)即分割結(jié)果中檢出的不屬于目標(biāo)的像素點(diǎn)數(shù)。一般地,較好的分割算法應(yīng)同時(shí)具備準(zhǔn)確性和完整性,因此要求漏檢點(diǎn)數(shù)和誤檢點(diǎn)數(shù)盡量小,即具有較高的正檢率和較低的誤檢率。此外,收斂時(shí)間越短越好。定義正檢率(rcd)和誤檢率(red)分別如下:

3.1 單目標(biāo)圖像
單目標(biāo)圖像第一組實(shí)驗(yàn)結(jié)果對(duì)比如圖5(C-V模型中隨機(jī)選取掩膜為[50∶250,100∶200])所示,實(shí)驗(yàn)數(shù)據(jù)如表1所示。第二組實(shí)驗(yàn)結(jié)果對(duì)比如圖6(C-V模型中隨機(jī)選取掩膜為[100∶300,50∶200])所示,實(shí)驗(yàn)數(shù)據(jù)如表2所示。

圖5 第一組實(shí)驗(yàn)結(jié)果對(duì)比Fig.5 The first set of results contrast
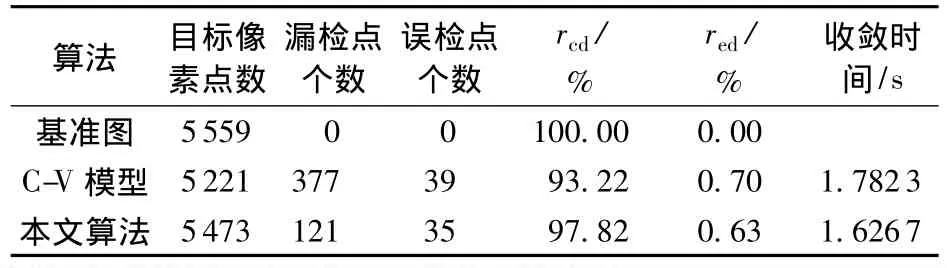
表1 第一組實(shí)驗(yàn)數(shù)據(jù)對(duì)比Table 1 The first set of experiments data contrast

圖6 第二組實(shí)驗(yàn)結(jié)果對(duì)比Fig.6 The second set of results contrast
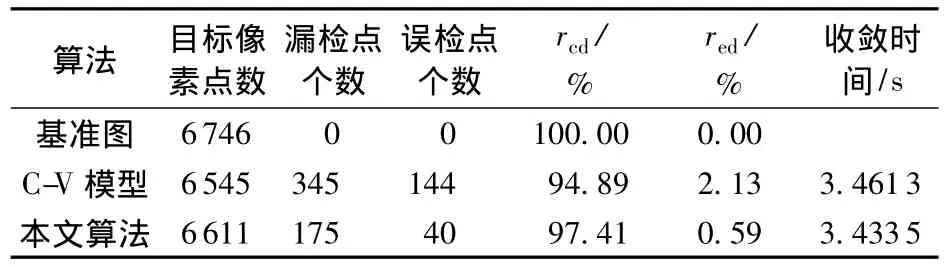
表2 第二組實(shí)驗(yàn)數(shù)據(jù)對(duì)比Table 2 The second set of experiments data contrast
表1為單目標(biāo)第一組實(shí)驗(yàn)的量化對(duì)比結(jié)果,由表中數(shù)據(jù)可以看出,本文算法的正檢率高于C-V模型的正檢率,且其誤檢率低于C-V模型。此外,通過觀察圖5也可以看出,在較短的時(shí)間內(nèi),本文算法分割出了更為完整且精確的目標(biāo)區(qū)域。觀察第二組實(shí)驗(yàn)結(jié)果及數(shù)據(jù)可知,本文算法與C-V模型相比擁有更高的正檢率和較低的誤檢率,符合目標(biāo)分割算法對(duì)完整性和準(zhǔn)確性的要求。并且,如圖6所示,在第二組實(shí)驗(yàn)中原始圖像含噪聲較多,傳統(tǒng)的C-V方法輪廓收斂過程中呈現(xiàn)不斷振蕩的狀態(tài),而本文算法則可以以較快的速度穩(wěn)定收斂,因此在復(fù)雜背景或是噪聲較多的圖像中本文算法優(yōu)勢(shì)更為明顯。上述兩組對(duì)比實(shí)驗(yàn)結(jié)果表明,本文算法不僅能夠自動(dòng)選取初始掩膜以實(shí)現(xiàn)完全自動(dòng)的分割,解決了傳統(tǒng)方法受主觀性影響較大的問題,而且可以有效地減少迭代次數(shù),能夠以更快的時(shí)間和更少的迭代次數(shù)收斂到邊界輪廓,并得到更為精確的分割結(jié)果。此外,本文提出的算法通過模擬人類視覺初始化掩膜,實(shí)現(xiàn)由粗到精的分割更加符合人類認(rèn)知機(jī)制。
3.2 多目標(biāo)圖像
圖7(C-V模型中隨機(jī)選取掩膜為[100∶300,100∶300])和表3分別為應(yīng)用三種不同方法對(duì)飛機(jī)圖像分割的結(jié)果及量化數(shù)據(jù)。由圖7可直觀看出,本文融合邊緣特征及顯著圖的算法取得了較好的分割效果,完整地分割出了目標(biāo),而隨機(jī)選取掩膜的C-V模型效果最為不理想。
觀察表3中的具體數(shù)據(jù),顯然本文基于顯著圖的算法和針對(duì)多目標(biāo)提出的基于融合邊緣特征及顯著圖的算法正檢率都高于C-V模型,而誤檢率則均遠(yuǎn)低于C-V模型。同時(shí),在相近的時(shí)間內(nèi),本文基于融合邊緣特征及顯著圖的算法的效果優(yōu)于基于顯著圖的算法。因此,本文算法能夠有效地取代手動(dòng)選取掩膜的方法,以實(shí)現(xiàn)顯著目標(biāo)的完全自動(dòng)分割。
對(duì)背景相對(duì)復(fù)雜的花朵圖像分別應(yīng)用三種不同的方法進(jìn)行分割實(shí)驗(yàn),結(jié)果如圖8(C-V模型中隨機(jī)選取掩膜為[100∶400,100∶500])所示。圖8中(f)、(g)、(h)表明本文融合邊緣特征的顯著圖算法效果最好,而C-V模型手動(dòng)選取的掩膜受主觀性影響較大。若選取不當(dāng),則極有可能漏檢目標(biāo),并且對(duì)于背景相對(duì)復(fù)雜含噪聲較多的圖像其收斂過程中不斷振蕩。前述的基于顯著圖的算法應(yīng)用于多目標(biāo)的分割時(shí),其初始掩膜由多個(gè)目標(biāo)的顯著圖構(gòu)成,可能會(huì)合成一個(gè)較大的區(qū)域,從而影響分割效率。觀察表4,顯然C-V模型的正檢率和誤檢率不夠理想,而本文融合邊緣特征的顯著圖算法則取得了較為理想的正檢率和誤檢率。其中,基于顯著圖算法的正檢率雖然稍高于本文算法,但是其誤檢率卻是本文算法的25.6倍。仔細(xì)觀察圖8可知,由于基準(zhǔn)圖為人工標(biāo)定的結(jié)果有一定誤差,而分割算法在迭代過程中能將邊緣細(xì)節(jié)分割出來,因此可能會(huì)造成少量的漏檢點(diǎn)。綜合考慮分割目標(biāo)的正確性、完整性可知,本文算法效果相對(duì)較好,能夠在多目標(biāo)圖像分割中自動(dòng)選取初始掩膜以實(shí)現(xiàn)完全自動(dòng)的分割,在一定程度上解決了傳統(tǒng)方法受主觀性影響較大的問題。

圖7 分別用不同方法迭代150次得到的輪廓以及分割結(jié)果Fig.7 Contour and segmentation results of 150 iterations with different methods respectively

表3 多目標(biāo)第一組實(shí)驗(yàn)數(shù)據(jù)對(duì)比Table 3 The first set of multi-target experiments data contrast

圖8 分別用不同方法迭代300次得到的輪廓以及分割結(jié)果Fig.8 Contour and segmentation results of 300 iterations with different methods respectively

表4 多目標(biāo)第二組實(shí)驗(yàn)數(shù)據(jù)對(duì)比Table 4 The second set of multi-target experiments data contrast
4 結(jié)束語
通過對(duì)主動(dòng)輪廓模型以及人類認(rèn)知機(jī)制的深入研究,將選擇性注意機(jī)制引入到基于區(qū)域的無邊界主動(dòng)輪廓模型中,并利用數(shù)學(xué)形態(tài)學(xué)算子對(duì)圖像進(jìn)行平滑預(yù)處理。此外,在多目標(biāo)情況下,將選擇注意與小波變換相結(jié)合初始化掩膜。實(shí)驗(yàn)結(jié)果表明本文算法是可行的,不僅可以減少迭代次數(shù),當(dāng)圖像中存在多個(gè)目標(biāo)時(shí)還可以得到更精確的分割結(jié)果,有效地提高了主動(dòng)輪廓算法的效率。
[1] KASS M,WITKIN A,TERZOPOULOUS D.Snake:active contour models[J].International Journal of Computer Vision,1988,1(4):321-331.
[2] COHEN L D.On active contour models and balloons[J].Computer Vision,Graphics and Image Processing:Image Understanding,1991,53(2):211-218.
[3] CASELLES V,CATTE F,COLL T,et al.A geometric model for active contours in image processing[J].Numerische Mathematic,1993,66:1-31.
[4] MALLADI R,SETHIAN J A,VEMURI B C.Shape modeling with front propagation:a level set approach [J].IEEE transactions on Pattern Analysis and Machine Intelligence,1995,17(2):158-175.
[5] CASELLES V,KIMMEL R,SAPIRO G.Geodesic active contours[J].International Journal of Computer Vision,1997,22(1):61-79.
[6] SADDIQI K,LAUZIERE Y B,TANNENBAUM A,et al.Area and length minimizing flows for shape segmentation [J].IEEE Transactions on Image Processing,1998,7(3):433-443.
[7] XU C,YEZZI A,PRINCE J L.On the relationship between parametric and geometric active contours[C]//34th Asilomar Conference of Signals,Systems,and Computers,2000.
[8] MUMFORD D,SHAH J.Optimal approximation by piecewise smooth functions and associated variational problems[J].Communications on Pure and Applied Mathematics,1989,42:577-685.
[9] CHAN T,VESE L.Active contour without edges for vector-valued image[J].Journal of Visual Communication and Image Representation,2001,10(2):266-277.
[10] STERNBERG S R.Grayscale morphology[J].Computer Vision Graphics,and Image Process,1986,35(3):333-355.
[11] SERRA J.Image analysis and mathematical morphology[M].Vol.II:Theoretical Advances,Chap.10.London:Academic Press,1988.
[12] KAELI J W,SINGH H,ARMSTRONG R A.An automated morphological image processing based methodology for quantifying coral cover in deeper-reef zones[C/OL]//2006 IEEE/MTS Oceans Conference,Boston,USA,September 18-21,2006[2013-02-10].http://ieeexplore.ieee.org/stamp/stamp.jsp?tp= &arnumber=4098975.
[13] 吳國良,楊浩,羅建.二維A Tuous算法圖像邊緣檢測(cè)研究[J].計(jì)算機(jī)工程與應(yīng)用,2010,46(11):167-169.
WU Guo-liang,YANG Hao,LUO Jian.Research of edge detection based on 2-D A Tuous algorithm[J].Computer Engineering and Applications,2010,46(11):167-169.
[14] 蔣欣.水平集方法及其在圖像分割上的應(yīng)用[J].上海生物醫(yī)學(xué)工程,2004,25(3):29-32,61.
JIANG Xin.Level set method and its application on image segmentation[J].Shanghai Journal of Biomedical Engineering,2004,25(3):29-32,61.

