改進的盲解卷積技術在遠距離激光光斑圖像復原中的應用

孫宏海，劉艷瀅

（1.中國科學院長春光學精密機械與物理研究所航空光學成像與測量中國科學院重點實驗室，吉林長春130033；2.中國科學院長春光學精密機械與物理研究所，吉林長春130033）

改進的盲解卷積技術在遠距離激光光斑圖像復原中的應用

孫宏海1，2*，劉艷瀅2

（1.中國科學院長春光學精密機械與物理研究所航空光學成像與測量中國科學院重點實驗室，吉林長春130033；2.中國科學院長春光學精密機械與物理研究所，吉林長春130033）

為了提高外場實驗中遠距離測量激光光斑位置的精度，提出利用盲解卷積技術對光斑圖像進行事后復原來削弱大氣湍流對光斑成像的影響。首先，介紹了經典盲解卷積算法，分析了其不足之處，并提出了一種改進的盲解卷積算法。為了提高目標函數的收斂性和收斂速度，在TV（Total Variation）目標函數加入懲罰項，并對交替迭代法進行改進。然后，用數學方法證明了改進的盲解卷積算法的收斂性。最后，進行了仿真實驗。與傳統算法相比，用改進算法恢復的圖像信噪比至少提升了15%。文中給出了外場試驗圖像的實際復原效果。

圖像復原；盲解卷積；TV算法；大氣湍流；激光光斑

1 引 言

在激光半主動末制導導彈、炮彈及炸彈等武器系統外場試驗時，常常利用激光照射器監測系統對激光照射器照射光斑的時序特性和空間特性進行監測，以檢驗激光照射器照射目標的精度。外場實驗時，大氣湍流擾動會使大氣介質的折射系數發生隨機波動，使激光光束在傳播過程中發生光學波前失真，產生光束漂移和光強閃爍等現象，嚴重影響激光光束在大氣中遠距離傳播后的激光光斑成像質量。紅外傳感器可以觀測到激光光斑圖像明顯的模糊退化現象。自適應光學技術［1］是消除大氣湍流對成像影響有效方法之一。在典型的自適應光學系統中，通過波前探測器探測到光學波前失真，控制系統驅動變形鏡對畸變波前進行補償，實時校正波前，可消除大氣擾動。天文等領域的一些應用經常使用自適應光學系統對模糊退化進行補償，但是自適應光學系統結構復雜，造價昂貴，故有些應用利用價格低廉的部分補償系統，但這種系統會導致相位錯誤。為解決上述問題，本文提出采用盲解卷積技術對激光光斑圖像進行事后圖像復原，削弱大氣湍流對光斑圖像的影響，從而提高計算激光光斑位置的精度。

2 盲解卷積介紹

在成像應用中，一幅觀測到的圖像，如果忽略加性噪聲，可以認為是源圖像f（x，y）和點擴散函數h（x，y）的卷積：

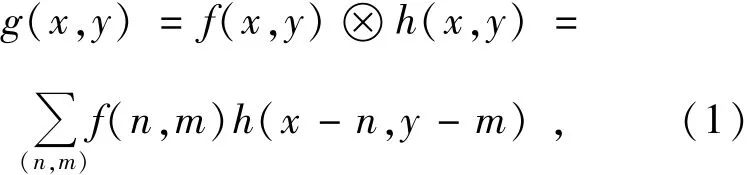
式中，?表示卷積算子。若用這些函數相應的大寫字母表示其傅里葉變換，那么式（1）的傅里葉變換可以表示為：

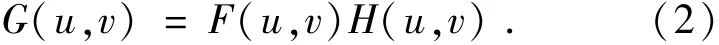
解卷積圖像復原方法應用很廣泛，例如天文光斑成像、遙感成像、醫學成像等。在大多數情況下，點擴散函數h（x，y）都作為先驗條件，這就是經典線性圖像復原問題。解決這類問題的解卷積方法很多［2］，如逆濾波、維納濾波、最小二乘濾波、遞歸卡爾曼濾波、約束迭代解卷積等。但是在解決實際問題時，點擴散函數通常很難精確地計算或測量；由于點擴散函數的隨機抖動很難定性，因此也無法精確建模。在實時圖像處理中，點擴散函數不能預先確定，而用于退化估計的在線識別技術也將會導致嚴重的錯誤。而且關于源圖像的可用信息也不多，想要獲得關于成像目標的先驗信息在物理上講，通常是不可能的。例如在遙感和天文應用中，很難通過統計對原始圖像建模，或者是得到之前從未觀測過的目標確切信息。將點擴散函數和待恢復的未知圖像從卷積g（x，y）中估計出來，這類估計問題就是所謂的盲解卷積問題，在改善圖像質量方面有廣泛應用。

經典盲解卷積方法有Ayers和Dainty提出迭代盲解卷積算法［3］（Iterative Blind Deconvolution，IBD），該算法通過迭代循環估計出源圖像，但是在求逆時會產生較大的誤差，而且使用“最陡下降法”進行搜索，收斂性較差。McCallum的模擬退火算法（Simulated Annealing，SA）［4］能夠在噪聲存在的條件下給出合理的解，其主要缺點是目標函數全局最小化的收斂速率很慢，算法的收斂速率在很大程度上依賴于溫度參數下降的速率，為了得到一個優秀解往往需要經過長時間的運算。以后Kundur提出了NAS-RIF（Nonnegativity and Support constraints Recursive Inverse Filtering）算法［5］，該算法的優點在于能夠保證在噪聲存在的條件下收斂于全局最小值解，而且收斂速度要比IBD算法快得多，但是該方法需要額外的約束條件支持，限制了應用范圍。TV（Total Variation）方法由Rudin［6］首先提出并用于圖像去噪，此后Tony等人［7］將TV方法用于圖像復原，基本形式為：

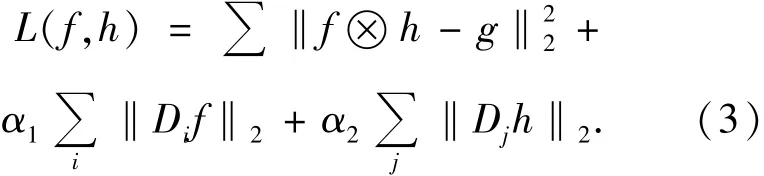
式中，Di是正則化算子，權值取常數合并到正則化參數α1和α2中。Dif和Djh表示源圖像和點擴散函數的離散梯度，其他一般微分算子（如Tikhonov-like算子）雖然可以將目標函數最小化問題轉化成較為簡單的線性系統方程求解問題，但是通常恢復后的源圖像過于平滑，很難保存圖像的某些特性，如明顯的邊緣等信息。但是由于TV函數的不可微和非線性等特點，對于式（3）的求解是困難的。上述方法為單幀盲解卷積方法，也可以利用多幀圖像盲解卷積，但是在盲解前需要對多幀圖像進行配準［8］，也可以對多幀圖像中的目標進行預測［9］，對圖像頻域添加新的約束［10］等方法。本文中需要復原的是光斑目標邊緣，而且只能夠利用單幀信息，因此本文對傳統TV方法進行了改進，并通過數學證明求得的改進的TV方法的解是收斂的。

3 改進的盲解卷積算法

3.1 目標函數的建立

為了提高目標函數的收斂速度和收斂性，采用懲罰機制對TV正則化方法進行改進，改進后的算法稱為PTV（Penalized Total Variation），如下式所示：

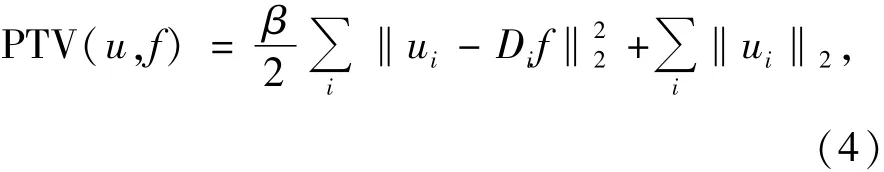
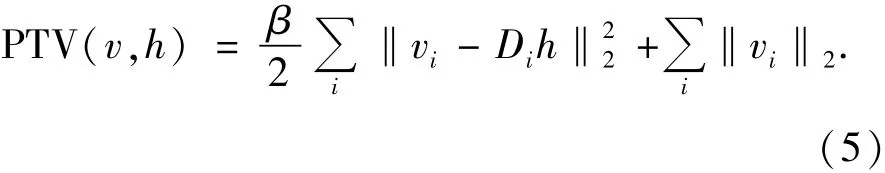
改進的算法中引入加入兩個變量u和v，β為懲罰系數；式（4）和式（5）中第一項為懲罰項；目標函數可以定義為：

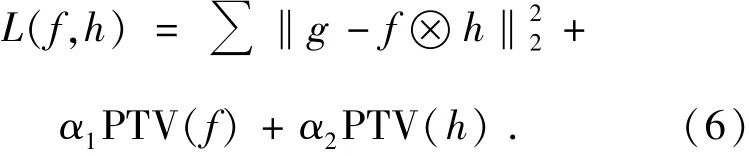
3.2 交替最小化方法

由于懲罰項的引入，增加了兩個新的變量，交替最小化方法也進行相應的改進，基本步驟為：

（1）給定初始值f00、h00及允許誤差ε；

（2）求h0使得下式取最小值：

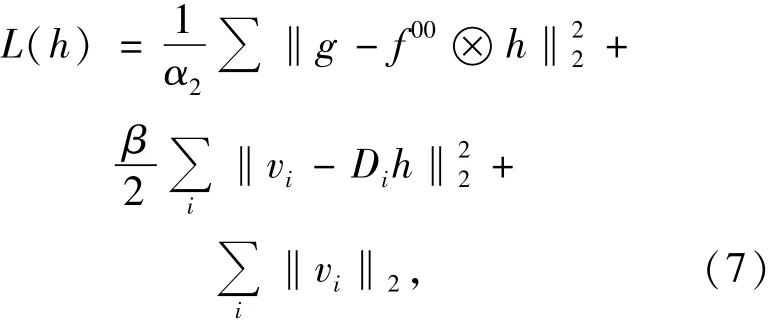
①利用初始值h00求v0，使得下式取最小值：

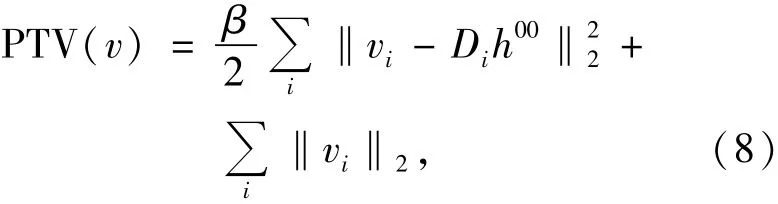
求解可得：

②利用得到的v0求h01，使得下式取最小值：

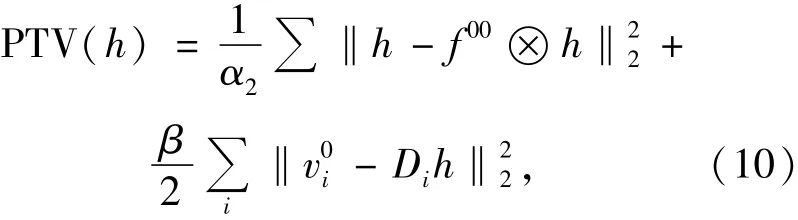
求解可得：

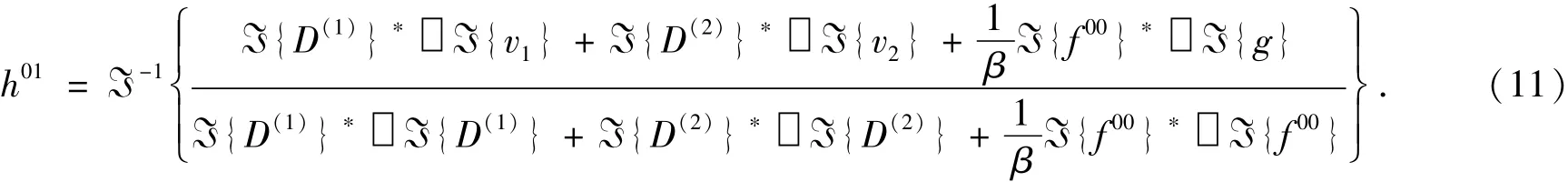
③驗證是否滿足PTV（v0，h01）＜ε，如果不滿足該條件則繼續循環；若滿足則使h0=h0n，繼續進行下一步算法。

（3）求f1使得下式取最小值：

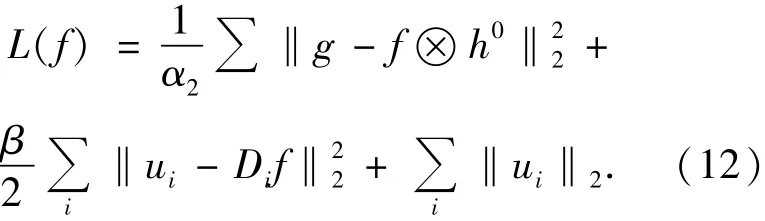
①利用初始值f10=f00求u0，使得下式取最小值：

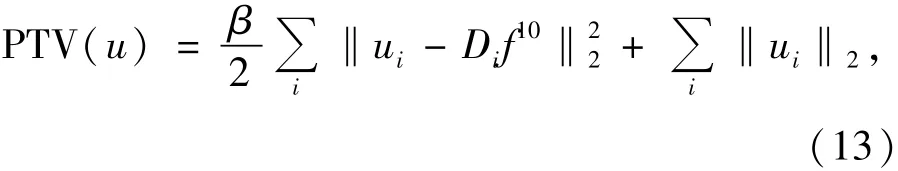
求解可得：

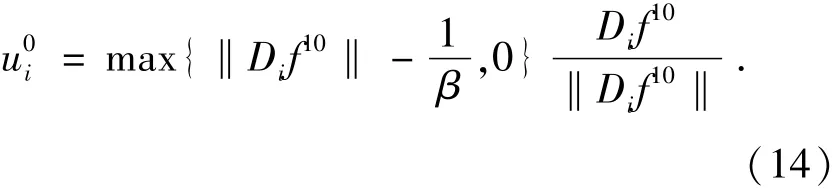
②利用得到的u0求f11，使得下式取最小值：

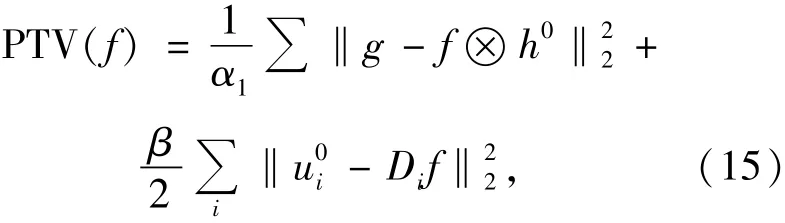
求解可得：

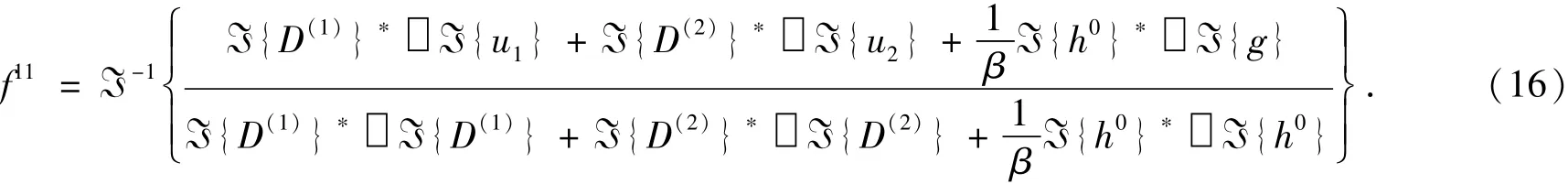
③驗證是否滿足PTV（u0，f11）＜ε，如果不滿足該條件則繼續循環；若滿足則使f1=f1n，繼續進行下一步算法。

（4）將f1和h0代入目標函數（6）中，驗證其是否滿足L（f1，h0）＜ε，如果不滿足則繼續循環；若滿足則停止循環。

改進的交替最小化算法中，“*”代表復共軛，“?”代表逐個元素取乘積。隨著β→∞，式（6）的解收斂于式（3）的解。下面將證明對于一個固定值β＞0改進交替迭代算法的收斂性。

3.3 改進交替迭代算法的收斂性

不難發現，改進交替迭代算法的收斂性等價于下面兩個問題的收斂性：

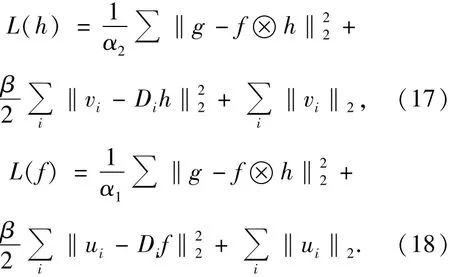
下面以證明式（17）的收斂性為例，即證明由上述改進交替迭代算法得到的序列｛（uk，fk）｝收斂到式（17）的解。定義一個收縮算子s：?2→?2，對于任意a∈?2，有：

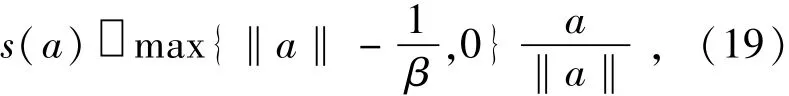
如果定義0?（0/0）=0，可以得到：

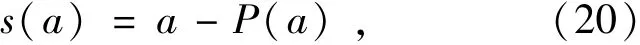
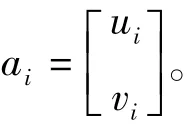
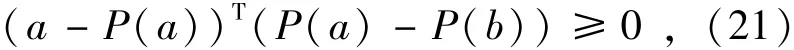
交換a，b可得：

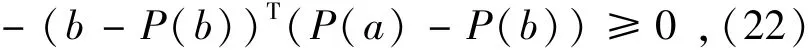
將兩式相加得：

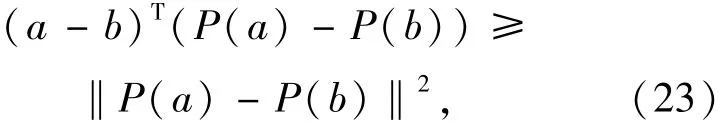
因此從式（20）可以得到：

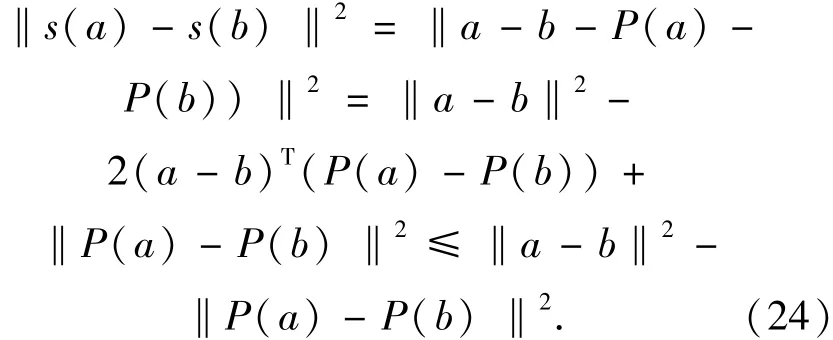
如果‖s（a）-s（b）‖=‖a-b‖，那么P（a）=P（b），s（a）-s（b）=a-b-（P（a）-P（b））。

定義兩個正定對稱矩陣：

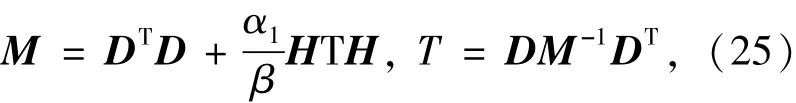
定義一個線性算子p：?2n→?2n2使得：

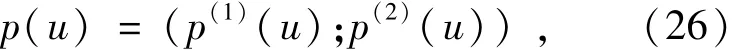
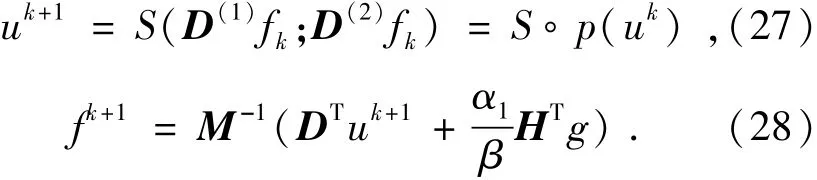
由于目標函數（17）是凸的、有下限界的，因此至少有一個最小化對（u*，f*）使得目標函數值隨著交替最小化迭代的進行不再繼續減小，則必須滿足：

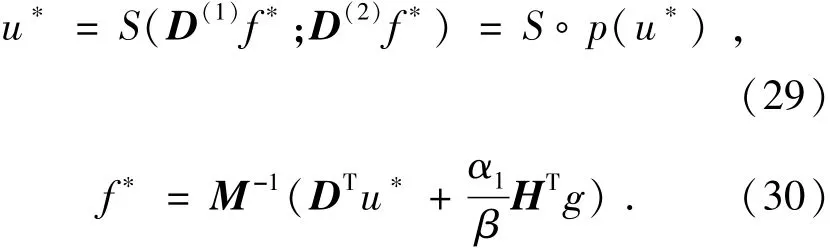
由式（29）可知序列｛uk｝位于一個緊集中，因此至少存在一個點，。設?為S?p的不動點即?=S?p（?），于是可得：

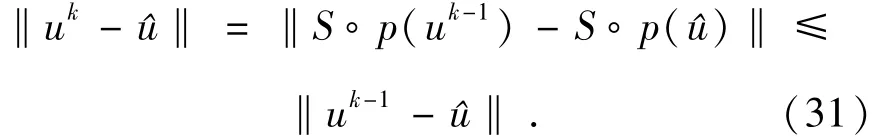
因此存在下面的極限：

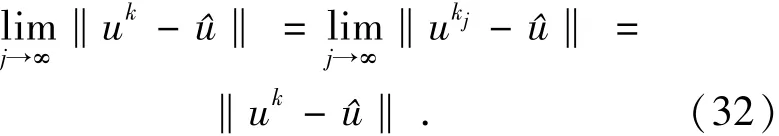
這意味著所有｛uk｝的極限點和?的距離都相等，由S?p的連續性可知：

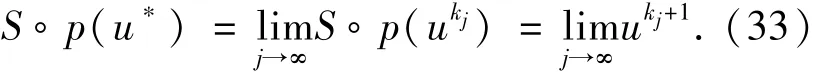
因此S?p（u*）是｛uk｝的一個極限點，和u*同樣與?的距離相等：

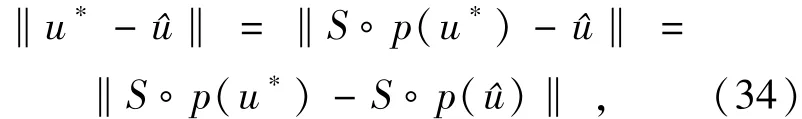
因為?是S?p任意不動點，用u*替換?，即可建立｛uk｝的收斂性：。同樣對于序列｛fk｝也將按式（28）收斂于某個f*，因此（u*，f*）滿足式（29）和式（30），是式（6）的一個解。

4 實驗結果與討論

本文提出一種改進盲解卷積迭代算法用于事后圖像復原，本小節進行一些仿真實驗來驗證算法的性能。這里采用Lena和Cameraman作為原始參考圖像，并設計兩個高斯函數作為使參考圖像退化的點擴散函數（Point Spread Function，PSF），如圖1所示。

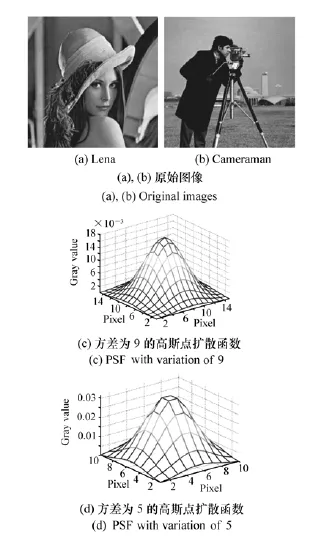
圖1 仿真實驗原始圖像和點擴散函數Fig.1 Original images and PSFs

試驗方法為：利用方差為9和5的高斯點擴散函數對參考圖像進行高斯模糊處理；為了驗證算法抗噪聲能力，同時加入模糊信噪比（Blured Signal Noise Ratio，BSNR）為40和20 dB的高斯加性噪聲，結果如圖2所示。

為了與采用不同事后圖像復原算法處理圖像進行恢復質量比較，采用以下準則：

（1）均方根誤差準則，假設圖像大小為M× N，則參考圖像R和復原圖像F之間的均方根誤差為：

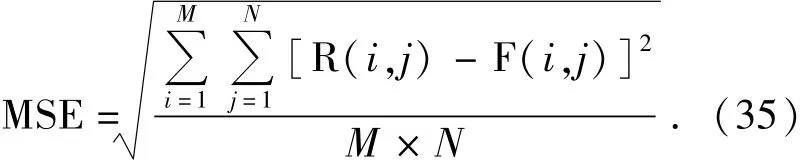
圖2 觀測圖像Fig.2 Observed images

均方根誤差值越小，說明算法所復原圖像質量越好。

（2）互信息準則，復原圖像F和參考圖像R的互信息為：

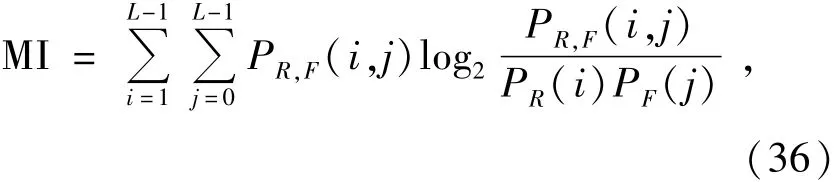
式中，PR為參考圖像R的概率密度，PF為復原圖像F的概率密度，PR，F為F和R的聯合概率密度，L為灰度級數。互信息越大，復原圖像的質量越好。

（3）改善信噪比（Improvement in Signal-to-Noise Ratio，ISNR）準則，反映了圖像的恢復質量，改善信噪比值越大，表示圖像復原質量越好。

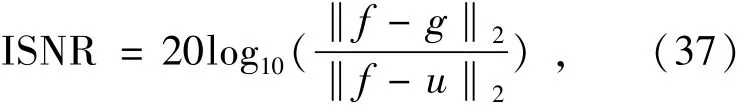
式中，f，g，u分別代表源圖像、觀測圖像和復原圖像。

圖3 恢復圖像Fig.3 Restored images

在本文實驗中，使用觀測圖像作為初始迭代圖像，使用δ函數作為初始點擴散函數。提出本文迭代算法約束條件，將迭代過程中點擴散函數和迭代圖像負值部分設置為零，迭代結束條件ε設定為1×10-4。得到改進算法恢復的圖像如圖3所示。

表1～4所示為利用IBD算法、TV算法，及本文提出的改進算法恢復的圖像結果，從表1～4中統計數據可以看出，本文提出的算法恢復圖像的效果都有明顯的提升，其中信噪比至少提高15%以上。

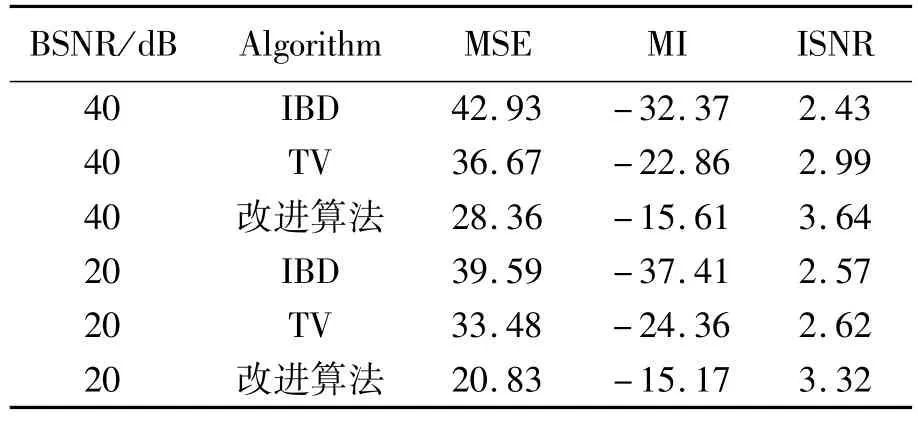
表1 高斯點擴散函數方差為9的Lena圖像復原與其它算法結果的比較Tab.1 Comparison of restored image Lena w ith different algorithm s（PSF variation is 9）

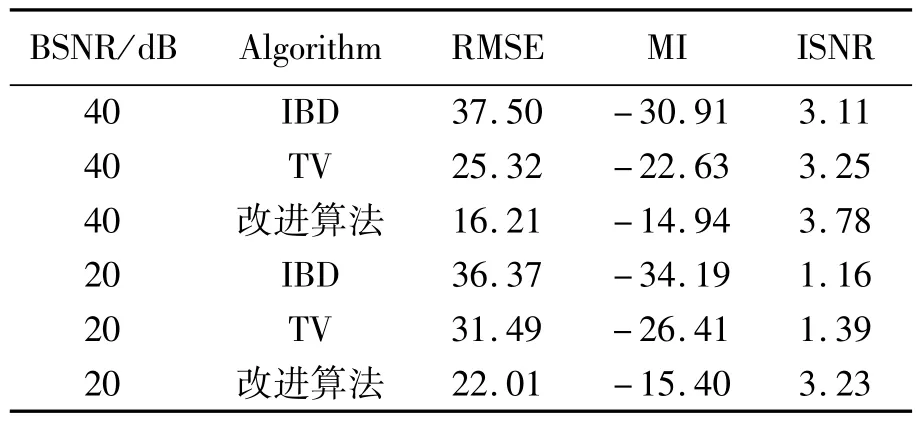
表2 高斯點擴散函數方差為5的Lena圖像復原與其它算法結果的比較Tab.2 Comparison of restored image Lena w ith different algorithm s（PSF variation is 5）

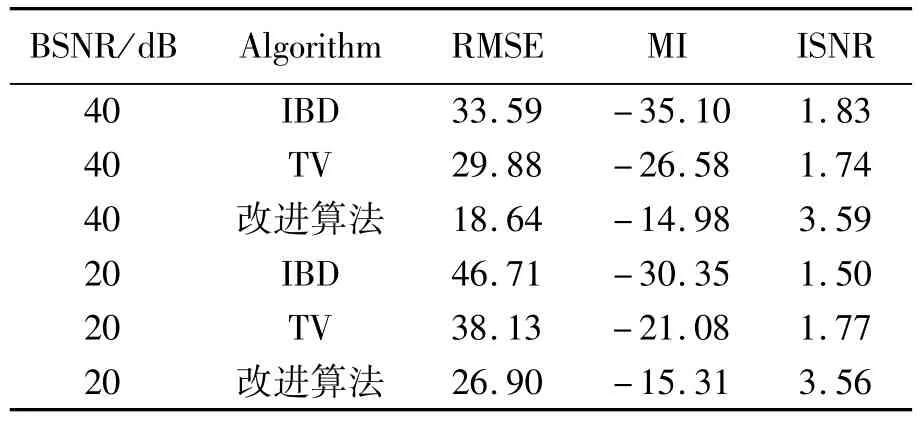
表3 高斯點擴散函數方差為9的Cameraman圖像復原與其它算法結果的比較Tab.3 Comparison of restored image Cameraman w ith different algorithms（PSF variation is 9）

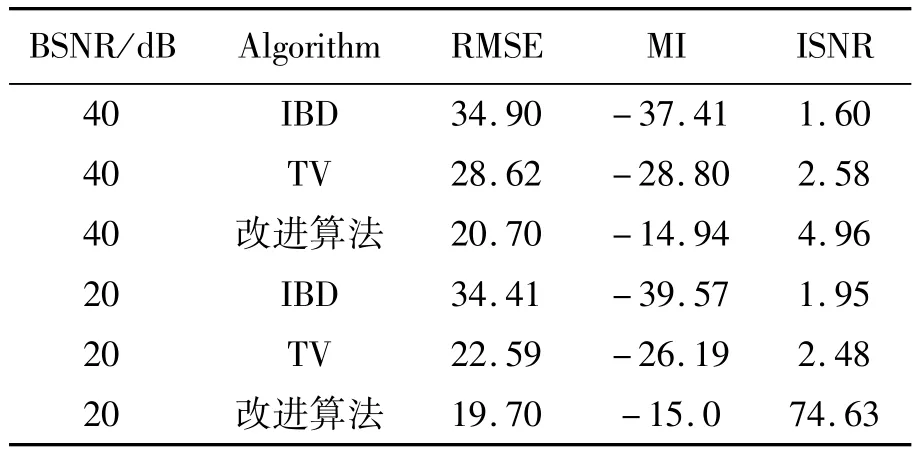
表4 高斯點擴散函數方差為5的Cameraman圖像復原與其它算法結果的比較Tab.4 Comparison of restored image Cameraman w ith different algorithms（PSF variation is 5）

從以上數據比較可以看出，本文提出的算法可以很好地復原仿真圖像。下面利用該算法對實際外場采集的激光光斑圖像進行復原，結果如圖4所示。

圖4 外場光斑圖像復原結果Fig.4 Restoration results of spot image

5 結 論

本文設計了一種改進的盲解卷積方法，并從數學上證明了算法收斂性。仿真實驗結果顯示，和經典盲解算法相比，改進方法的性能具有一定的優越性；從實際外場采集到的光斑圖像復原效果顯示，光斑邊緣變得清晰，這時再利用細分定位算法計算光斑位置，可以獲得較高精度。

參考文獻：

［1］ 陳波.適應光學圖像復原理論與算法研究［D］.北京：解放軍信息工程大學，2008. CHEN B.The theory and algorithms of adaptive potics image restoration［D］.Beijing：PLA Information Engineering University，2008.（in Chinese）

［2］ LANE R G.Blind deconvolution of speckle images［J］.J.Opt.Soc.Am.A，1992，9（9）：1580-1587.

［3］ AYERSG R，DAINTY JC.Iterative blind deconvolutionmethod and its applications［J］.Opt.Letters，1988，13（7）：547-550.

［4］ KUNDUR D，HATZINAKOSD.Blind image deconvolution［J］.IEEE Signal Processing Magazion，1996，4（3）：43-65.

［5］ KUNDUR D，HATZINAKOSD.Blind image restoration via recursive filtering using deterministic constraints［J］.IEEE，1996：2283-2287.

［6］ RUDIN L，OSHER S，FATEMIE.Nonlinear total variation based noise removal algorithms［J］.Physica D，1992，60：259-268.

［7］ CHAN T，GOLUBG，MULETP.A nonlinear primal-dualmethod for TV-based image restoration［J］.Proc.12thInt.Conf. Analysis and Optimization of Systems：Images，Wavelets and PDE′s，1996，219：241-252.

［8］ 宋向，耿則勛，王洛飛.基于SIFT特征配準的多幀迭代盲解卷積算法［J］.測繪科學，2011（6）：109-111. SONG X，GENG Z X，WANG L F.Multi-frame iterative blind deconvolution based on the SIFT feature registration［J］. Sci.Sureying and Mapping，2011（6）：109-111.（in Chinese）

［9］ 邸男，付東輝，王毅楠.利用加權預測的圖像迭代盲解卷積［J］.中國光學，2011（5）：514-518. DIN，FU D H，WANG Y N.Iterative blind deconvolution of image with weighted prediction［J］.Chinese Optics，2011（5）：514-518.（in Chinese）

［10］ 王洛飛，耿則勛，魏小峰.結合Fourier域約束的多幀盲解卷積圖像恢復算法［J］.測繪科學技術學報，2011（4）：283-287. WANG L F，GENG ZX，WEIX F.Multi-frame blind deconvolution algorithm based on Fourier-constrained［J］.J.Geomatics Science and Technology，2011（4）：283-287.（in Chinese）

［11］ 溫博，張啟衡，張建林.應用自解卷積和增量Wiener濾波實現迭代盲圖像復原［J］.光學精密工程，2011（12）：3050-3056. WEN B，ZHANG Q H，ZHANG JL.Realization of iterative blind image restoration by self deconvolution and increment Wiener filter［J］.Opt.Precision Eng.，2011（12）：3050-3056.（in Chinese）

［12］ 母一寧，劉泉，于林韜，等.哈特曼技術在序列光斑檢測中的應用［J］.光學精密工程，2011（9）：2197-2194. MU Y N，LIU Q，YU L T，et al..Application of Hartmann technique in sequence spot detection［J］.Opt.Precision Eng.，2011（9）：2197-2194.（in Chinese）

Application of improved blind deconvolution technology in long-ranged laser spot image restoration

SUN Hong-hai1，2*，LIU Yan-ying2
（1.Key Laboratory of Airborne Optical Imaging and Measurement，Changchun Institute of Optics，Fine Mechanics and Physics，Chinese Academy of Sciences，Changchun 130033，China；2.Changchun Institute of Optics，Fine Mechanics and Physics，Chinese Academy of Sciences，Changchun 130033，China）
*Corresponding author，E-mail：shh426@gmail.com

To improve the precision of long-ranged laser spot positionmeasurement in an outdoor experiment，blind deconvolution technology was proposed to restore the spot image afterwards to lower the impact of atmospheric turbulence on spot imaging.First，classical blind deconvolution algorithms were introduced，of which the shortage is analyzed.Second，an improved blind deconvolution algorithm was designed.The penalty terms were added to TV（Total Variation）objective function and the alternative iterativemethod was also redesigned. Then，the convergence of the improved method was testified mathematically.Finally，the improved methodwas compared with other classicalmethods by experimental simulation.The capability of improvedmethod was testified with several objective figures，and the results show that the Signal to Noise Ratio（SNR）is improved by 15%at least.The restoration result of outdoor experiment proves that the improved method is effective.

image restoration；blind deconvolution；Total Variation（TV）algorithm；atmospheric turbulence；laser spot

TP391.4

A

10.3788/CO.20130606.0868

孫宏海（1980—），男，吉林長春人，博士，副研究員，主要從事數字圖像處理和高速成像與實時處理系統方面的研究。E-mail：shh426@gmail.com

劉艷瀅（1965—），女，吉林長春人，碩士生導師，研究員，主要從事數字圖像處理方面的研究。E-mail：liuyy@ciomp.ac.cn

1674-2915（2013）06-0868-08

2013-09-10；

2013-11-16

國家高技術研究發展計劃（863計劃）資助項目（No.2012AA7031010B）；吉林省重大科技攻關資助項目（No.11ZDGG001）