在研究和學習中追尋數學本義

就數學教學而言，我覺得更多地應該由“靜態”的數學向“動態”的數學轉移。在教學中，教師應將學生置于學習的主體地位，通過精心設計的數學活動線索，引導學生深入地思考、探尋和理解知識與觀點背后的價值意義，促進他們主動思考、積極思辨與自我建構，發展思維，生長智慧。

“用計算器探索積的變化規律”這一節課，主要是借助計算器讓學生經歷探索規律、發現規律的一般過程，體驗探索規律的一般策略與方法，發展數學思考，提升數學素養。通過對教學內容的審視與透析，不難發現，“計算器”“探索”和“規律”是本課的三個關鍵詞。其中，“計算器”是學生探索的工具；“規律”是學生探索的結果；“探索”才是教學的“核心”。基于上述認識，筆者設想架構一條充滿探索味和研究味的教學思路，讓學生在有效探索和自主學習中發展數學思維，實現數學教學的本真意義。以下是新授環節教學實踐的簡要描述：

一、建立猜想

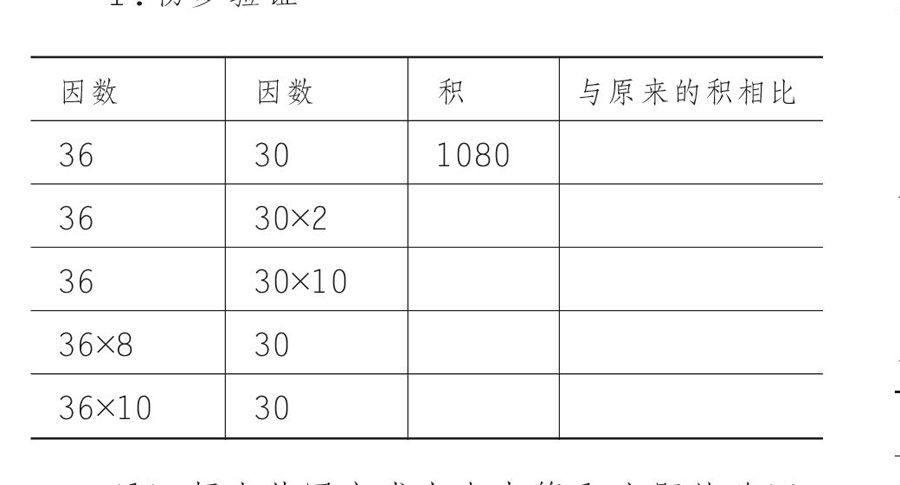
1.計算器計算出36×30的積，體會36、30和1080在乘法算式中的名稱。

2.猜想：如果其中的一個因數不變，另一個因數乘一個數，得到的積可能會有什么變化？教師根據例題分層出現表格，在小組討論中初步形成對問題的猜想。

3.通過大組交流，進一步明晰猜想。即“一個因數不變，另一個因數乘幾，得到的積等于原來的積乘幾”。

【意圖：結合例題直接提出猜想，首先基于學生過去相關問題計算的經驗，從規律探索的角度引發學生對經驗的回顧和提升；其次，點明了本課核心的探索線索，體會“猜想—驗證”的數學思想方法。】

二、驗證猜想

1.初步驗證

（1）師生共同完成上表中第1小題的驗證，重點體會驗證的方法和結果。

（2）小組合作完成其余3小題的驗證，強調小組內分工合作的重要性。

（3）交流匯報驗證的方法和結果，體會到上表中的4小題通過驗證，都符合先前的猜想。

（4）質疑：通過對上表的探索和驗證，是否可以認定猜想一定是成立的？通過交流，引發學生進一步驗證的需求。一是在36×30=1080這個式子中進一步驗證，二是在其它乘法式子中進一步驗證。

2.再次驗證

（1）出示表格，引導學生對36×30=1080這個乘法式子繼續展開研究，進一步驗證猜想是否成立。

（2）交流驗證的過程，體會猜想結果的正確性。在交流中，重點擇取數目大的，數目小的以及如0和1等一些特殊的數，體會舉例驗證時數據的合理性和豐富性。

（3）小結：在36×30=1080這個乘法式子中，通過研究發現：一個因數不變，另一個因數無論乘幾，從驗證的過程和結果上看，都符合猜想。

3.豐富驗證

（1）出示表格，讓學生換一個乘法式子繼續展開研究，再次驗證猜想是否成立。

（2）學生自由舉例驗證，匯報交流，再次確認猜想成立。

三、歸納提升

1.小結：通過大量舉例，發現都符合先前的猜想，由此可確認猜想成立。帶領學生回憶此規律在筆算乘法中的運用。

2.反思：引導學生回顧整個研究過程，突出規律研究的一般方法，體會數學思想方法。

【意圖：體會驗證方法的合理性，強調驗證結果的正確性，凸顯驗證過程的豐富性是本環節教學的核心。學生在學習中，心理和認知上都有了不斷的提升，既對自己的猜想獲得初步的成立感到成功的喜悅，又對自己的驗證進一步產生“質疑”。不僅強調了“做數學”的過程，又突出了培養良好“數學素養”的重要性。伴隨著思路的“打開”，行為也就變得“清晰”和“有序”了。學生經歷的不僅是設計方法、發現規律的過程，更經歷了不斷感知，不斷體悟數學思想、數學方法的過程。“結論”是“有效過程”催化的結果，“有效過程”是追尋“數學本義”的核心。[1]】

回顧本課的設計思路，筆者從追尋數學本義的角度，力圖使數學學習過程變成學生主體性、能動性、獨立性不斷發展和提升的過程，從而真正實現授受式學習向自主探究式學習的轉變。具體來說，借助本課教學，追尋數學本義，關鍵體現四個“注重”。

一、注重結果和過程的和諧統一

對于學生而言，接受并發現積的變化規律并不難，但是如果教學直指獲得規律這一結果，而淡化或削弱規律的探索過程，那么教學目標就會發生偏移。規律固然重要，但是規律是怎么來的更加重要，這對學生的發展有著“結果”所無法替代的功能與價值。教學中，我著力讓學生體悟探索的線索，體會探索的一般方法，以36×30=1080這個式子為探索素材，建立猜想，然后再進一步進行引思：由36×30=1080這個式子得到的其他例子是否符合猜想？其他的乘法算式是否符合猜想？從簡單數據到復雜數據，從一般數據到特殊數據是否還符合猜想？學生在不斷的設計和驗證中逐步確認猜想，探索過程十分豐富，而就是在這一豐富而又充實的過程中，實現了結果和過程的和諧統一。

二、注重學習方式的有機融合

新課程改革背景下，當教師對學生進行重新認識與重新定位后，就開始用導學、參與、激勵、引領等方式去改進和豐富原有的教學方式。實際上，我們不僅要改變教師自己的教學方式，而且在改變自己教學方式的同時要關注學生的學習方式，并指導學生學習方式的改變。本課教學中，獨立思考、自主探索、合作交流等學生有效數學學習活動的重要方式，在教學過程的不同階段得以落實凸顯，既各有側重，又有機融合。

對于積的變化規律，在提出猜想后，驗證階段最初是師生合作，再后是小組合作的方式，而因數乘上非指定數目以及在其它乘法式子中的驗證，又完全由學生個體獨立完成。為了讓學生看到更多的舉例驗證的情況，又引導學生將自己舉例的情況在小組里進行集中觀察、討論和歸納。教學中，結合學生的認知實際，關注并豐富學生的學習方式，讓數學與活動有機融合，可以有效地促進學生對規律探索的體驗與理解。

三、注重數學思想的體驗感悟

數學思想蘊涵在數學知識形成、發展和應用的過程中，是數學知識和方法在更高層次上的抽象與概括，有助于學生形成良好的認知結構，有助于真正提高學生的數學素養并使他們終身受益。教學中筆者力求通過猜想規律——計算給定的題組——在比較觀察中初步發現規律——自主舉例進一步驗證規律——交流中確認規律等一系列過程，讓學生自然地體會到數學學習中常用的不完全歸納的一般過程，滲透了數學的思想與方法。

更重要的是，通過及時的回顧，使學生有效積累數學活動經驗，通過回顧發現規律的過程：觀察實例、大膽猜想、小心驗證、發現規律，為后續研究打下扎實的基礎。學生在這一過程中獲得的不僅僅是簡單意義上的“結論”，更是“結論”怎么來的過程，是數學方法的內化，所有這些都強調了數學教學的本真意義。學生經歷這樣的過程，不僅有助于積累探索規律的經驗與方法，更有助于進一步去發現其他的數學規律，并逐步形成發現規律的敏銳眼光。

四、注重凸顯教師的價值引導

課堂教學是以學生為主體、教師為主導的雙邊性教學活動，注重通過教師的主導促進學生認知，在互動中學習新知。教學中如果展現的僅僅是學生膚淺表層的甚至是虛假的主體性，而失卻教師的價值引導、智慧啟迪和思維點撥，必然導致課堂的低效甚至是無效。所以，教師的引導是實現師生交往互動、溝通交流、理解與對話的重要手段，是培養學生獨立思考、合作交流能力的重要途徑，也是教學取得良好效果的關鍵所在。[2]

基于本節課的教學目標和重難點，在教學中，我注意加強價值的引導，適時、適度地引領學生進行探究，由淺入深地探索數學方法和數學思想。當學生初步建立猜想時，教師及時引導學生思考：“猜想如不成立可以怎么辦？”當學生以算式36×30為例，驗證了4道小題時，教師又追問：“現在能不能確定猜想正確？你還擔心什么？”當學生發現自己所舉的例子符合猜想時，教師及時換角度引導學生思辨：“有沒有不符合猜想的例子？”當學生在練習中有了“新”的發現，教師又引導學生展開思考：“如果建立一個新的猜想，是怎樣的？怎樣來驗證？”等等，充分發揮了教師的引導作用。

我非常欣賞賁友林老師的一句話：“教學，并不是在已經繪制完畢的地圖上旅行，而是在旅行中完成地圖的繪制。”用計算器探索積的變化規律一課，正是在教師有目的、有計劃和有步驟的教學過程中，將學生或朦朧或隱蔽的認識打開，去審視，去分析，去發現，實現數學知識的意義建構，數學思想的體悟和數學活動經驗的積累。

參考文獻：

[1]黃榮德.在學習中研究和發展.教學研究和評論[J]，2011（6）.

[2]胡德運、陳燕.例談教師引導的設計.教學與管理[J]，2009（5）.

（黃榮德，無錫市洛社中心小學，214100）

責任編輯：宣麗華