核電站DCS系統歷史數據壓縮算法的研究
龍海軍 姚光霖
摘 要:本文通過對有損壓縮和無損壓縮的分析,給出一種二次數據壓縮方法,統一有損壓縮和無損壓縮的應用,對歷史庫的數據進行壓縮。試驗表明,此方法到達了數據壓縮的目的,又完整地保留了邏輯壓縮后的數據信息。
關鍵詞:核電站DCS Historian數據壓縮 模擬量數據壓縮 改進旋轉門數據壓縮
中圖分類號:TM862 文獻標識碼:A 文章編號:1672-3791(2013)03(b)-0029-02
1 研究背景
核電DCS控制系統中的歷史數據庫需要具備較高實時性、海量數據吞吐量的特點,因此在長時間系統運行的前提下,會產生巨大的歷史數據量,如果將這些數據直接存儲,不僅會浪費很多的存儲空間,而且還會使得數據查詢、傳輸變得復雜而困難。因此,將數據壓縮技術引入到DCS系統的歷史數據處理中,可以達到節省存儲空間、增加庫容量和提升系統運行效率等優勢。
2 數據壓縮技術簡介
歷史數據庫的數據壓縮是傳統數據壓縮技術在DCS工控領域的特殊應用,一般數據壓縮算法可以分為無損壓縮和有損壓縮兩種技術。
有損壓縮技術是根據特定的應用領域而發展起來的,它的基本原理是在數據壓縮過程中損失一定的信息以獲得較高的壓縮比,并且壓縮過程不可逆,壓縮后的數據不能完全地恢復到原始狀態,因此需要保證損失的數據對于理解原始數據信息特點的影響不大。具體到工控行業使用較多的壓縮算法包括:Hale和Sellars共同提出的矩形波串法(Box Car)和后向斜率發(Back ward Slope),以及在工控領域應用最為廣泛的OSIsoft公司提出的“旋轉門數據壓縮算法(Swing Door)”[1,2]。
無損壓縮技術是利用數據的統計冗余進行壓縮,可完全回復原始數據而不引起任何失真,但壓縮率是受到數據統計冗余度的理論限制,一般為2∶1~5∶1。這類方法廣泛用于文本數據,程序和特殊應用場合的圖像數據(如指紋圖像,醫學圖像等)的壓縮。無論是無損壓縮還是有損壓縮,都在工控領域的歷史數據處理中得到了應用,例如美國的Instep公司開發的實時歷史數據庫系統eDNA就實現了以Huffman為基本的無損數據壓縮程序,它首先對數據集合進行統計分析,將數據添加到Huffman樹中進行編碼,最后保存生成編碼,完成對數據群的壓縮;而OSIsoft公司的PI實時歷史數據庫產品采用了“旋轉門數據壓縮算法”以及獨到的二次過濾技術。
本論文所闡述的歷史數據(Historian)壓縮模塊,我們綜合了兩種壓縮算法的優劣,設計了一套“二次數據壓縮”機制,統一無損壓縮和有損壓縮算法應用,對歷史庫模擬量數據的壓縮。下面我們就具體來看些歷史數據(Historian)壓縮算法的設計。
3 歷史數據(Historian)壓縮模塊的設計
歷史數據(Historian)支持的數據類型包括開關量數據和模擬量數據。由于不同的數據類型所表現的數據特點的不同,需要設計針對性的壓縮策略來滿足各種數據的壓縮要求。
3.1 開關量數據壓縮
開關量數據采用“變化壓縮算法”,算法基本的設計思路是:當測點的數值發生變化時才會保存,否則丟棄當前數據。這是因為開關量測點的狀態一般由特定的0或1來表示,在DCS生產現場,有很多開關量測點的狀態在特定甚至是很長的時間內是不會發生變化的,所以“變化壓縮算法”非常適合對歷史庫開關量數據的壓縮處理。
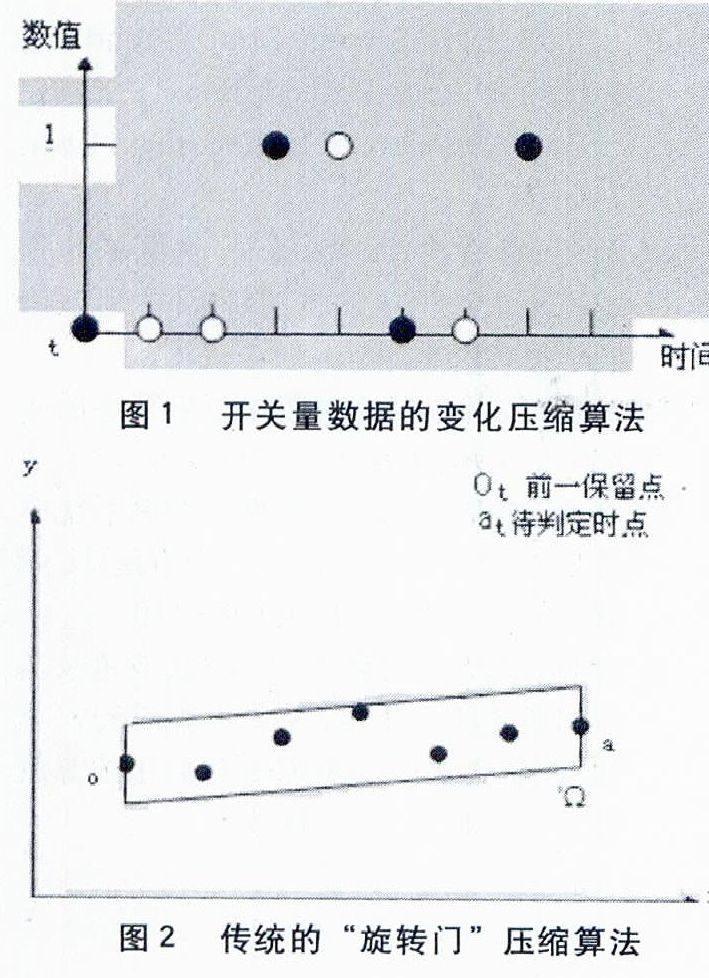
如圖1所示,設置某開關量測點每1秒進行一個數據值采集,以時刻點t為基準的后8s里,其測點值分別為0、0、0、1、1、0、0、1。根據“變化壓縮算法”的計算,剔除其在2 s、3 s、5 s和7 s的數據,只保存1 s、4 s、6 s和8 s的數據值。而當進行數據還原時,空缺時刻的數據值取前一保存時刻的數據,例如,2 s和3 s的數值均等于1 s數值0。這樣即完整的保存了測點在時間軸上的數據特征,又起到了節省存儲空間的目的。
3.2 模擬量數據壓縮
在DCS系統中的模擬量測點數據一般都會遵循一定的漸變規律,例如有的時間段會呈現較為一致的線性變化,有的時間段的數據特征為一條拋物線等。這些數據特征就給定了我們做歷史數據邏輯壓縮的前提。
在歷史數據(Historian)系統中,我們采用雙重的歷史數據壓縮機制,即“二次數據壓縮”,實現流行的“旋轉門”壓縮算法為第一層邏輯壓縮,實現無損的Huffman壓縮算法為第二層物理壓縮。首先來討論下傳統的“旋轉門”壓縮算法的內容。
3.2.1 傳統的“旋轉門”壓縮算法
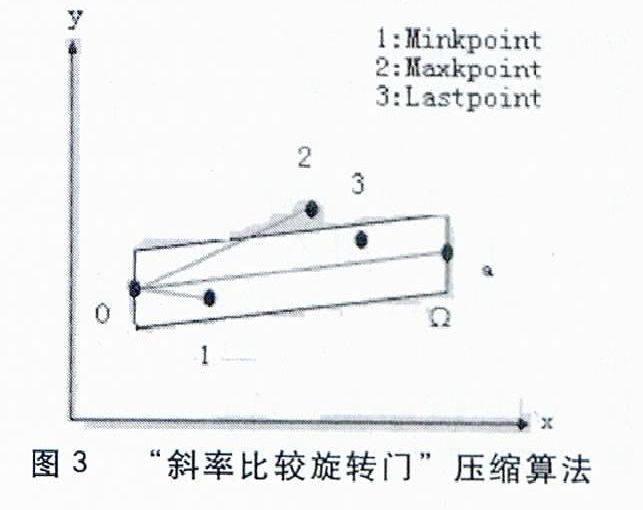
如圖2所示,基本的“旋轉門壓縮算法”是這樣描述的:在進行數據壓縮時,算法將新的實時數據點和前一個被保留的數據點之間做一個平行四邊形的偏移覆蓋區,如果這一平行四邊形可以覆蓋保留數據點之后出現的所有數據點時,那么將不會保存新的實時數據點。反之如果有任何一個數據點落在壓縮偏移覆蓋區外,則新數據點的前一個點將被保留,同時整個壓縮偏移覆蓋區將被重置,以新的被保留點作為新的起點,進入下一輪的旋轉門判斷[3]。
傳統的“旋轉門”壓縮算法雖然可以較好的完成對實時歷史數據的壓縮,但是在算法的實現和執行過程中會出現一些問題,主要體現在以下兩點。
(1)算法實現時需要一個臨時緩沖區來存儲待判定點集,但是在代碼實現時,這一緩沖區的大小缺失無法事先確定的。
(2)如果待判定點過多,緩沖區里的數據點數過大,那么在進行覆蓋區判定時會耗去系統過多的業務執行時間,造成系統運行的瓶頸。
因此,在以上算法的基礎上,我們采用了改進的“旋轉門”壓縮算法,即“斜率比較旋轉門”算法[4,5]。
3.2.2 改進的“斜率比較旋轉門”壓縮算法
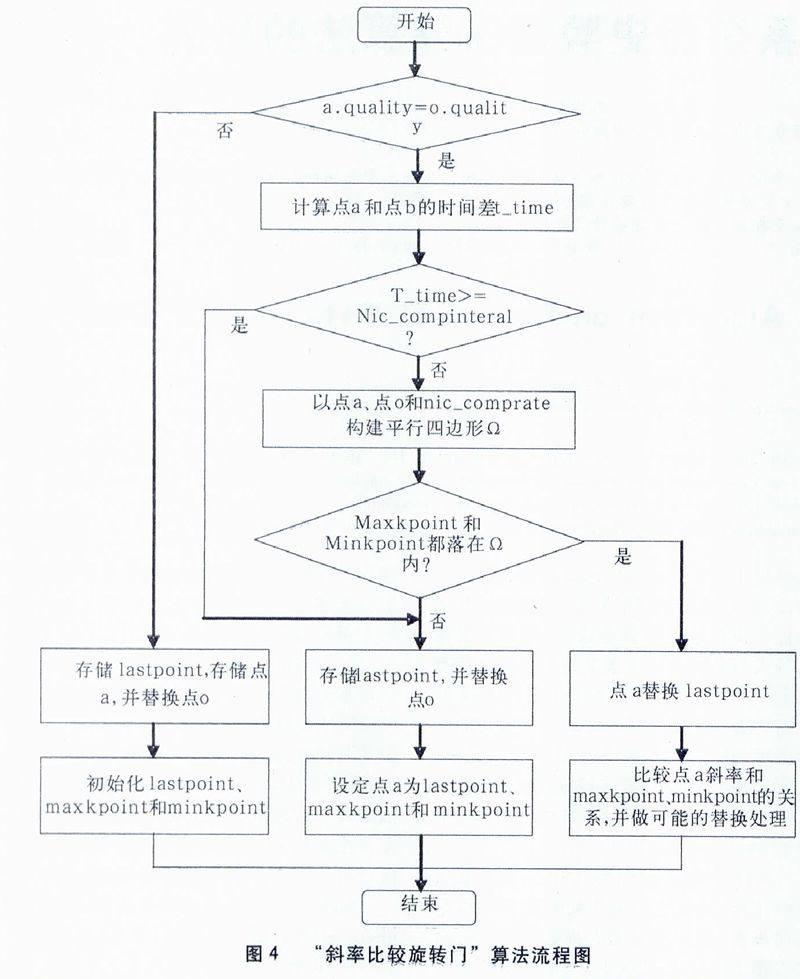
如圖3所示,當新點a到來時,系統會比較a與原點o(即上已存儲的點)的時間差t_time,如果t_time不小于壓縮間隔上限nic_compinterval或者a點質量戳與o點不同,則直接保存lastpoint點,進入下一輪旋轉門算法運算;否則以點a和o以及設定好的nic_comprate構建平行四邊形Ω,計算最大斜率點maxkpoint和最小斜率點minkpoint是否均在Ω內,計算結果有兩種。
(1)都落在了Ω內部,則說明a點通過了旋轉門,成為最新的lastpoint,最后再分別比較a點斜率與最大、最小斜率的關系,大于最大斜率值或者小于最小斜率值則替換掉相應的斜率點和斜率值,進入下一輪旋轉門算法運算。
(2)如果有一個斜率點落在了Ω外部,則說明a點沒有通過旋轉門,那么就保存此時的lastpoint,并將lastpoint點設定為下一輪旋轉門算法的o點,a點設定為最大和最小斜率點,進入下一輪旋轉門算法運算。
改進的“旋轉門”算法的具體流程圖如圖4所示。
以上介紹的“旋轉門”壓縮算法是系統第一次對歷史數據的邏輯壓縮,當經過邏輯壓縮后的保留數據積累到一定的數量時,例如1k,再對其進行第二次的物理壓縮。物理壓縮采用的是Huffman無損壓縮算法,它的基本原理是,構建一個用于字符編碼的Huffman二叉樹,根據待壓縮數據二進制子串出現的頻率對其進行排列,出現頻率大的串使用較少的位表示,較小的串使用較多的編碼來表示,這樣既到達了數據壓縮的目的,又完整地保留了邏輯壓縮后的數據信息。
4 結語
通過對無損壓縮算法和有損壓縮算法的對比分析研究,我們充分利用了兩種算法的優點,設計了“二層壓縮”算法,同時將“二次壓縮”算法應用于歷史數據(Historian)壓縮模塊的設計和實現中,形成了一種較為先進的技術實現手段,在工程應用中取得了良好的效果。
參考文獻
[1] 高寧波,金宏,王宏安.歷史數據實時壓縮方法研究[J].計算機功能與應用,2004,28:167-171.
[2] Bristol,E.H.Swing Door Trending: Adaptive Trend Recording,ISA National Conference Proceedings,1990:749-753.
[3] 蔣鵬,黃清波,王智,等.一種新的化工過程歷史數據壓縮方法研究[J].浙江大學學報,2005,39(6):814-818.
[4] 徐慧.實時數據庫中數據壓縮算法的研究[D].杭州:浙江大學,2006.
[5] 馮磊,李俊,夏雨人.計算機控制系統中歷史數據存儲與查詢的一種方法[J].計算機工程,2003,29(3):108-110.
[6] 黃靜.LZW壓縮算法VC實現、改進及其應用研究[D].長沙:中南大學,2007.李湘.分布式實時數據庫及數據壓縮算法研究[D].北京:北京科技大.

