基于均勻角點匹配的基礎矩陣估計方法

羅桂娥，李 映

（中南大學 信息科學與工程學院，湖南 長沙 410083）

在計算機視覺與圖像處理中，基礎矩陣（F矩陣）[1-2]可用來表示最基本的對極幾何關系，基礎矩陣是聯系同一場景所拍攝的兩幅圖像之間的重要橋梁，對基礎矩陣F的估計是三維重建、運動估計、攝像機標定、匹配與跟蹤的基礎[3]。求解基礎矩陣時，首先是提取特征點，再對其進行匹配。傳統的Harris提取的特征點存在聚簇現象，本文在Harris角點提取中加入了鄰近點剔除策略，最終能得到分配較為均勻的匹配特征點對。在使用經典8點法[4]計算基礎矩陣時，采用平均值法計算基礎矩陣，從而有效提高基礎矩陣的精度。

1 角點提取方法

1.1 經典Harris角點檢測算法

經典 Harris算子[5]表達式如式（1）所示：

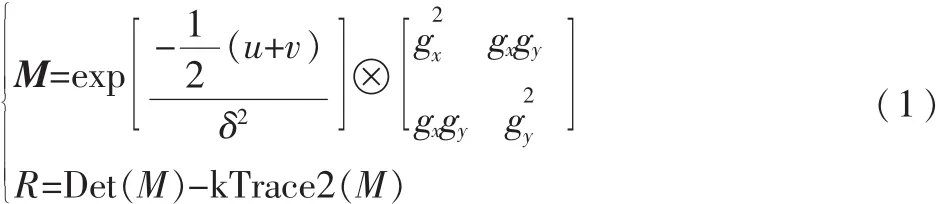
其中，M為亮度自相關矩陣，gx為 x方向梯度，gy為 y方向的梯度，G（s）為高斯模板，R為響應函數，k為默認常數，一般取值為0.04，角點即函數取得局部極大值時的點。

1.2 均勻Harris角點的提取

首先，按經典Harris角點監測算法計算圖像中存在角點的R值，將R值從大到小進行排序，選取較大的部分點作為最終的角點。為防止在局部區域出現角點簇擁的現象，本文采用鄰近點剔除策略減弱或消除這種方法。具體做法是：選用一個5×5模板對圖像進行處理，若在該模板下存在不止一個角點，則只保留R值相對較大的角點。

1.3 角點提取效果對比

試驗中采用鳳凰祼眼3D立體相機 （phenix SDC-821）構成雙目立體視覺系統，如圖1所示。將攝像機所采集到的圖像經分離之后得到左右圖像。圖2是所得圖像未進行鄰近點剔除所得146對匹配點圖像，圖3為所得圖像通過鄰近點剔除所得的138對匹配點圖像，明顯可以看出圖3所獲得的匹配角點對分布更為均勻。

2 基礎矩陣的計算

加入鄰近點剔除策略之后，計算各圖像的匹配點對，對其進行分組（每 8對為一組），由 8點算法[6]可求得第i組的基礎矩陣Fi，以每組得到的基礎矩陣求平均值作為最終值，如式（2）所示：

3 實驗結果及其分析

根據上述方法計算基礎矩陣，首先對雙目系統采集的平面圖像進行分割，提取左右攝像機所拍攝的圖像；再對灰度化后的平面圖像進行Harris角點提取以及鄰近點剔除；然后對角點進行匹配，計算出基礎矩陣F；最后采用平均余差 （ARE）[3]的方法來計算基礎矩陣的精度。基礎矩陣F的精度越高，平均余差值越小，如式（3）所示，其中 N為角點匹配數目，Ii，I′i分別為左右圖像第i個角點的齊次坐標。

表1是角點匹配點數與8點法和改進8點法求得的平均余差值之間的關系，圖4是表1所對應的曲線圖，由圖4可以看出，改進的8點算法明顯比一般8點法的余差值要小，因此，改進的8點法精度更高。

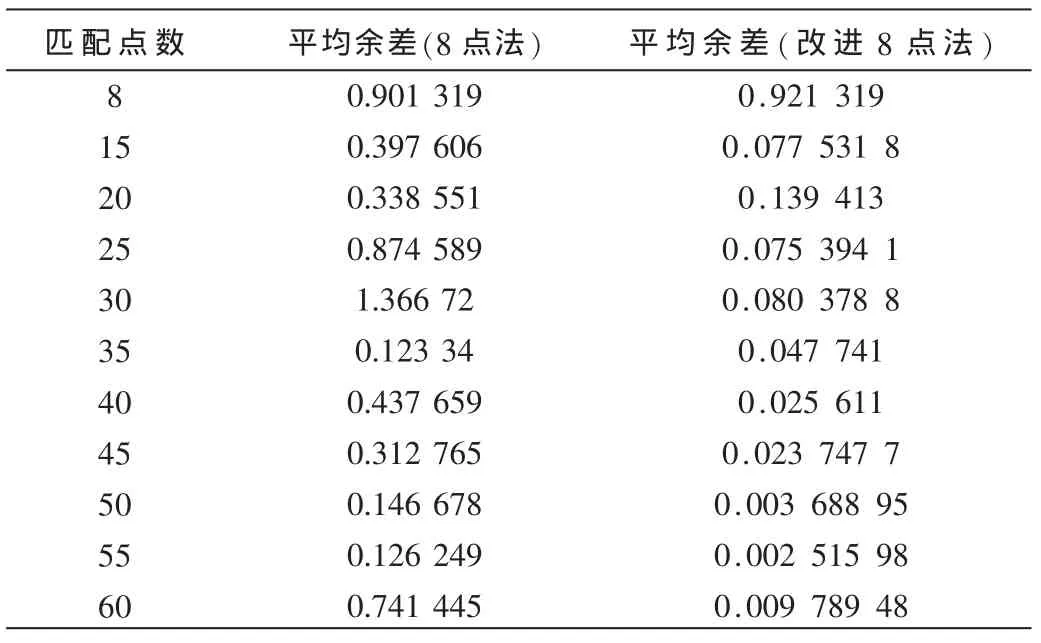
表1 匹配點數與平均余差關系

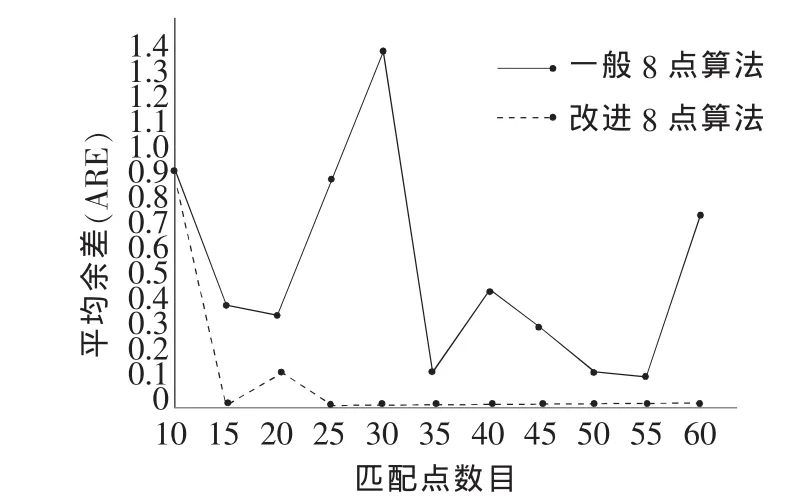
圖4 平均余差曲線圖

本文對基本矩陣的求解進行了研究，對使用Harris檢測算子提取的角點，通過引入鄰近點剔除策略從而提取到分布較為均勻的角點。通過對匹配點對進行分組求取基礎矩陣，以平均值為最終值能有效的保證基礎矩陣F的精度，用平均余差來計算基礎矩陣的精度，實驗結果表明，采用改進的8點算法對均勻角點求解基礎矩陣，其精度可以明顯較高。

[1]吳福朝.計算機視覺中的數學方法[M].北京：科學出版社，2008.

[2]陳付幸，王潤生.基礎矩陣估計的聚類分析算法[J].計算機輔助設計與圖形學學報，2005，17（10）：2251-2265.

[3]孫亦南，劉偉軍，馬永壯，等.一種加權計算基礎矩陣的高精度算法[J].計算機工程，2005，31（15）：186-188.

[4]Longuet-Higgins H C.A computer algorithm for reconstructing a scene from two projections[J].Nature， 1981， 293（9）：133-135.

[5]劉忠紅，儲珺.特征提取與模板匹配結合的圖像拼接方法[J].微計算機信息，2010，1：117-118.

[6]HARTLEY R.In Defense of the 8-point Algorithm[J].In：Grimson E （Ed.）， Proceedings of the 5thInternational Conference on Computer Vision， Cambridge： IEEE Computer Science Press， 1995： 1064-1070.